排序算法学习整理四（归并）
好久好久没有更过这种博客了，原本打算是大一下就把排序算法学完全部，顺便更新完博客的。但是被骗去硬件了（我这个蒟蒻，捧着一块15，还在傻傻的乐呵つ﹏⊂）。一拖就给忘了，果然脑子不太好使。
之所以，今天想起写排序算法的博客，是因为再PAT上遇到了一道@#%！的题目（点刚刚地方转跳），用到了插入和归并，写这道题的翻到了自己的插入排序的博客😂。
归入正题，这次讲的是归并排序。归并排序呢是一个非常有意思的排序算法，它与前三种排序不太一样，往常的排序都是，两个循环控制整个数组，进行为序调整，平均时间复杂度为T(n) = O(nlogn)。而归并排序呢，为了彰显自己非同凡响的思路，ta先将数组在逻辑上切成了n部分（n>1），然后一块块的处理，并且ta 的空间复杂度为O(N)。整个思想呢就是大名鼎鼎的 “分治” ，切就是 “分”， 处理就是 “治”。（可能这么说不太准确，接着会有比较官方的定义）顺便科普一下分治：分治法将问题 分(divide) 成一些小的问题然后递归求解，而 治(conquer)则将分的阶段得到的各答案"修补"在一起，即分而治之
来自百度百科的对归并排序的说明：
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个 子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序是一种稳定的排序方法。
我个人对上面这段话的解读如下：
1、归并排序的基础是归并操作（《数据结构》中的链表归并操作）
2、归并排序采用了分治法
3、归并排序多次将数组划分为等长的子序列（最大容差为1），并多次归并子序列
4、归并排序可以有n路归并，书中lef + (right - left) / 2 仅仅是归并排序 n = 2 的一种特殊情况，当然归并n表的函数需要重写。
瞎叨叨这么多，不如看张图来体会一下归并函数是如何排序的
(先来张动态的,如有侵权，请在下方评论)
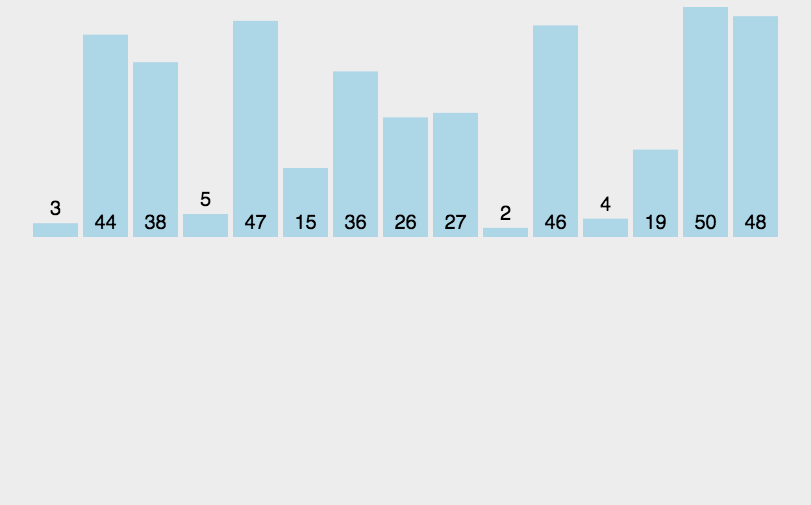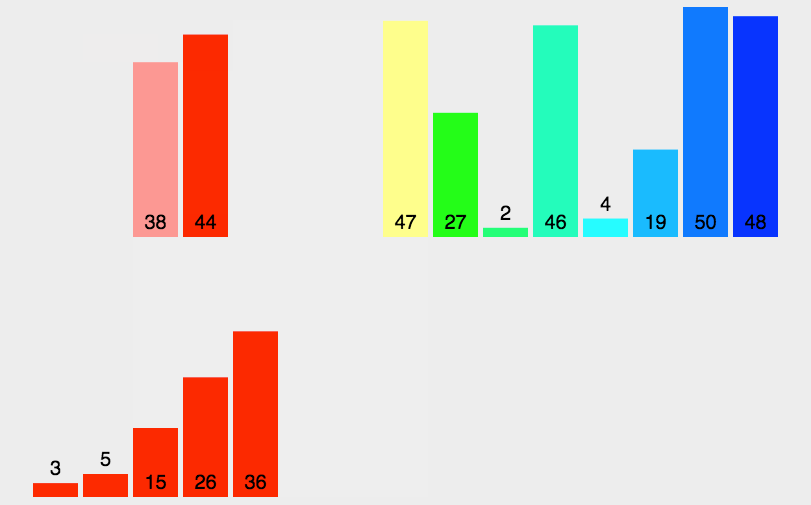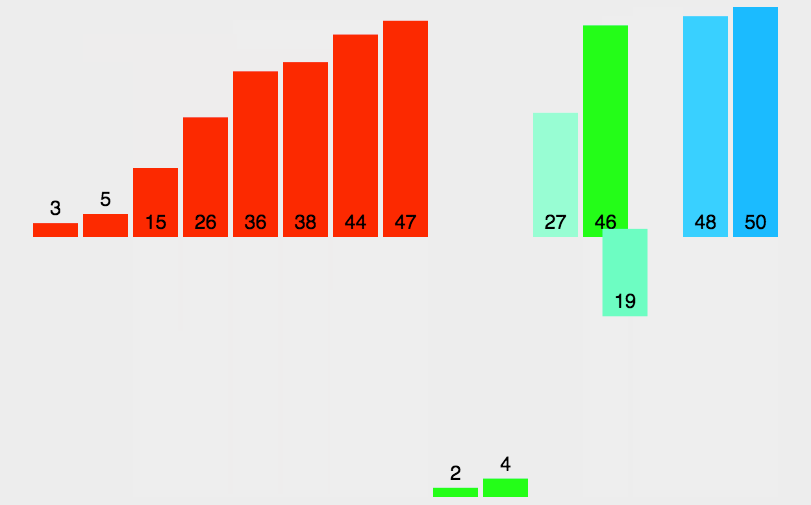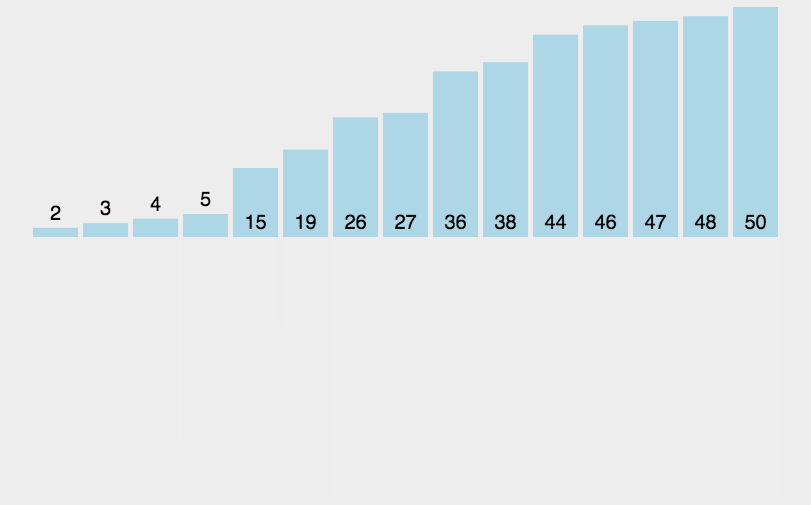
再来张静态的
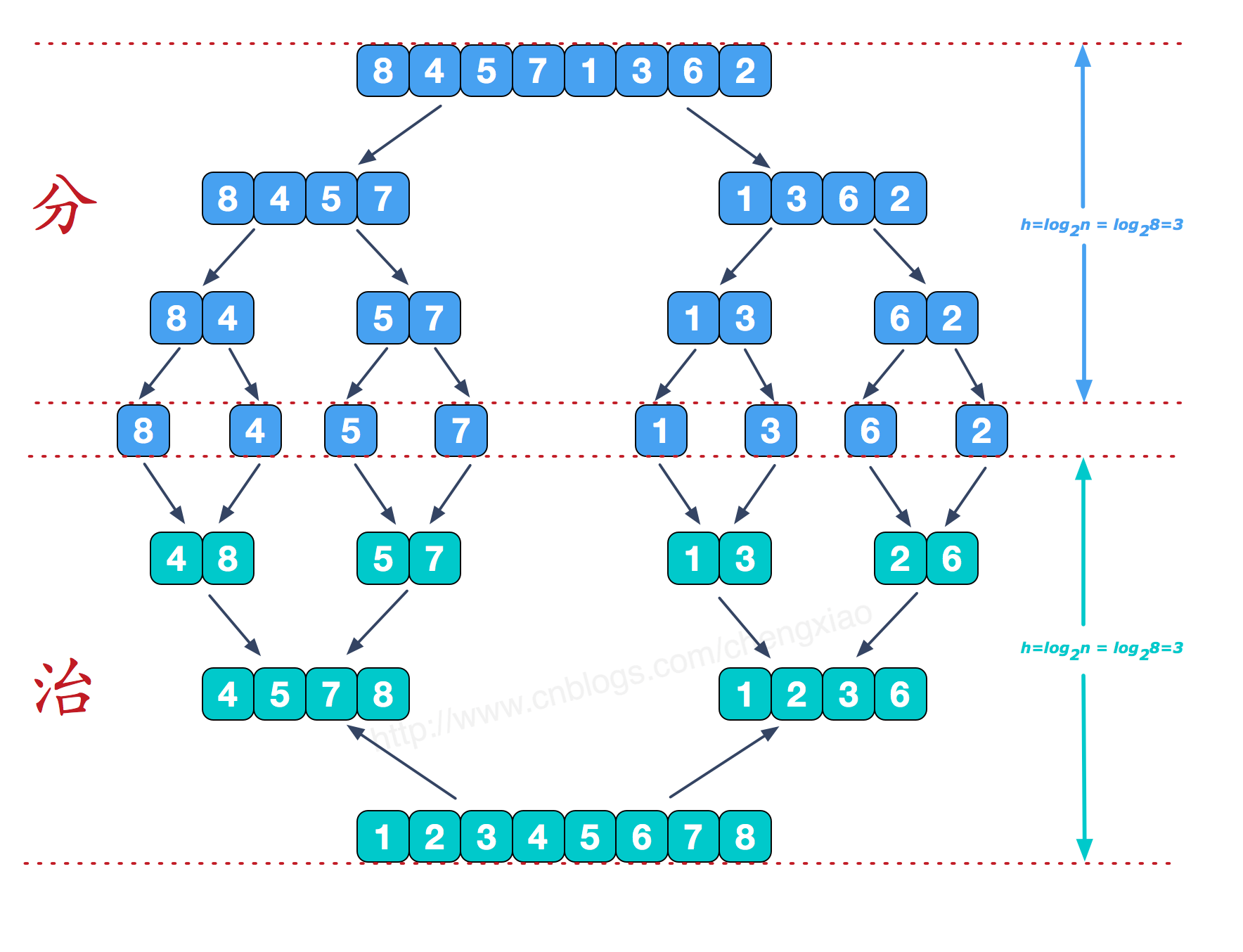（图片l来自：https://www.cnblogs.com/chengxiao/p/6194356.html）
从图中，我们可以清晰的看到，和我们刚刚说的那样。先把数组分成n个等长的子序列，然后一次次的归并（这是二路归并）。很明显每一个长度大于1的子序列都可以作为被分割的序列，继续分割，很明显的递归思想。（其实我特别想说，特像一棵完全二叉树，肯定可以递归实现）递归深度为log2n。动态图展现的思路是错的，但是递归的过程的确如动态图所示。
归并排序的核心：“分”和“治” 该如何实现呢？
我们先来分析一下“分”：
因为是二路分治，所以每次取数组中间部分。设n为数组长度，我们来推导一下：
第一次：mid1 = 0 + (n - 0) / 2；
左边 ：0 ~ mid1 ；右边：mid1 + 1 ~ n-1；
第二次：完了，分成两半了，凉凉，不然，先考虑一边的情况
mid2 = 0 + (mid1 - 0) / 2;
左边 ：0 ~ mid2 ；右边：mid2 + 1 ~ mid1 ；
第三次：mid3 = 0 + (mid2 - 0) /2；（同样，先考虑左边）
左边：0 ~ mid3 ；右边：mid3 + 1 ~ mid2
……
嗯~ o(*￣▽￣*)o，感觉没什么说服力ヽ(*。>Д<)o゜，来看张图吧
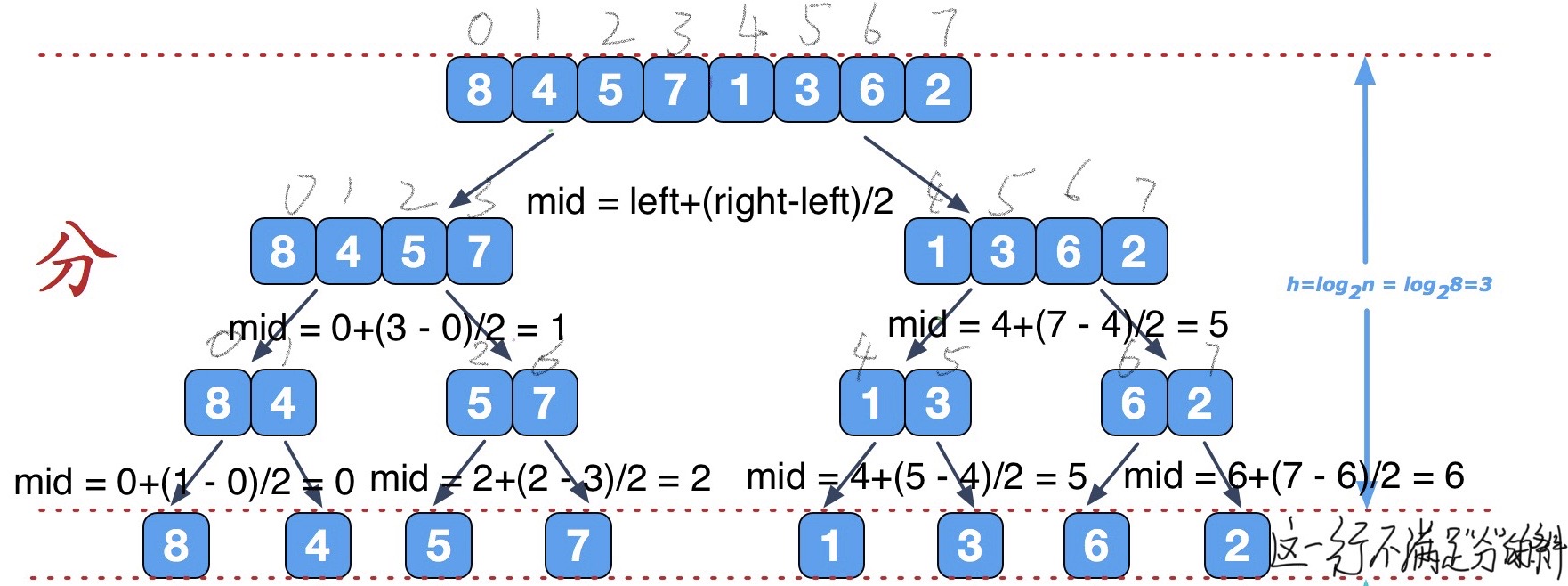
不难发现我们的对半的规律是 (子序列的终止地址 - 子序列的起始地址) / 2，那么咱们把开始地址定义为left ，终止边界定义为right，很显然，求mid的公式为就如图中所示
mid = left +（right -left）/ 2；
那么递归的终止条件呢？让我们来想想归并排序子序列可分的基本要求是什么？
子序列长度大于1，(总不能把一个元素砍成一个个字节来玩吧)。
那么这又意味着什么呢，left - right > 0; 即 left > right。
所以得出的 “分” 这部分的代码为：
1 void mergeSort(int arr[], int left, int right, int *temp) 2 { //实现“分” 3 if (left >= right) 4 {//停止条件 5 return; 6 } 7 8 int mid = left + (right - left) / 2; 9 mergeSort(arr, left, mid, temp); //从left ~ mid 10 mergeSort(arr, mid + 1, right, temp); //从mid+1 ~ right 11 mergeAdd(arr, left, mid, right, temp); //从这里是 “治” 的函数，分完就治理嘛 12 }
接着我们来分析一下“治”：
从最上面分治的流程图可以很明显的知道，“治” 的核心在于将子序列合并后有序化，那怎么样才能在合并的过程中有序化呢。前面我提到过归并排序的空间复杂度为O(N)。前三大排序空间复杂度为O(1)。嗯？
那里多出来的一组数据大小的空间？莫非ta开了一个一模一样的数组？
没错，归并的确新开了一个数组，大小为数据大小，用于存储有序化后的子序列。就像 8 和 4 这个两个长度为1的序列就是新创造出来的，一次类推，都是如此，就以流程图为例子，在 "治" 的过程中产生了8 个长度为 1 的子序列，然后通过递归的回溯，和 并称了长度为2，4的子序列，和最终结果长度为8的数组。但是切割数组再交换实实现起来，有点麻烦（主要是懒，好吧，其实嫌这种方法太慢了）。而且在递归中多次动态开辟空间很浪费时间，所以我决定只开辟一次数组，然后将临时数组当作参数传入函数。说真的，切割序列这玩意我觉得给吧，链表排序挺好的。
说了这么多就是想强调一点：我们需要一个临时数组用来存储排序好的子序列，然后塞回给原数组。
那么这一步是如何实现的呢？
以流程图为例子，最终排序结果为升序：
这里只有最后一步的图，一步步画到最后太麻烦了(/▽＼)
最后一步需要归并的子序列如下
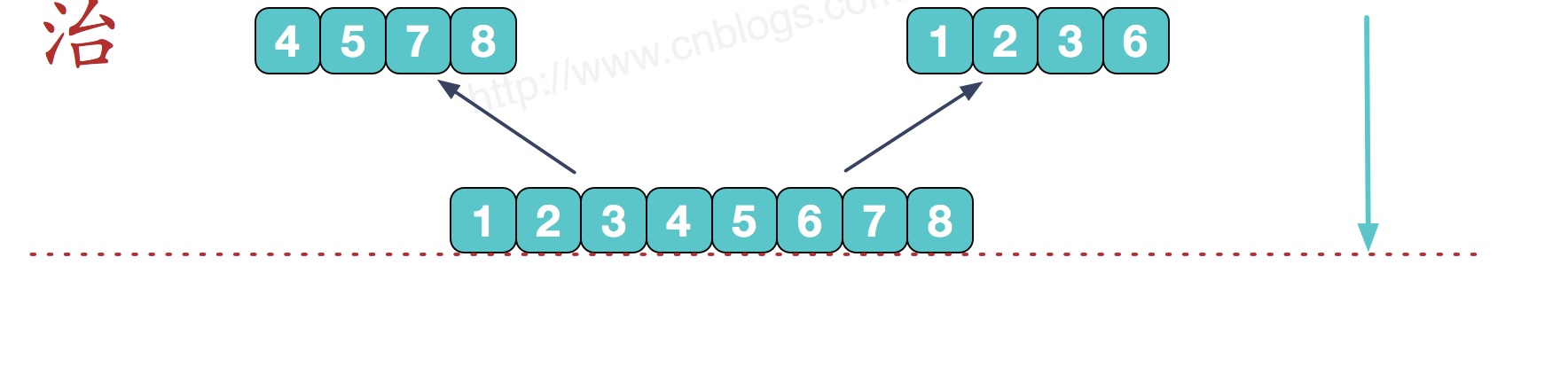
第一步：
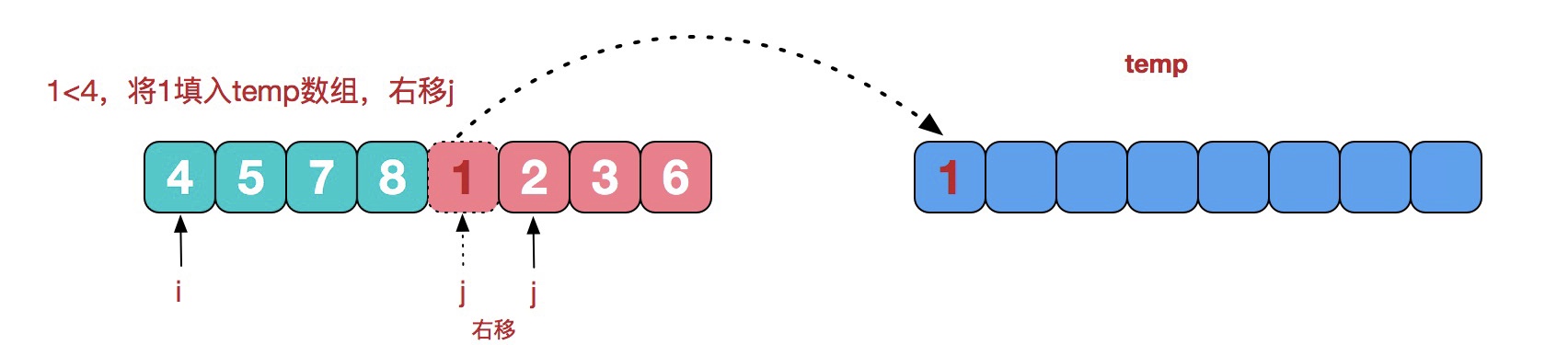
第二步：
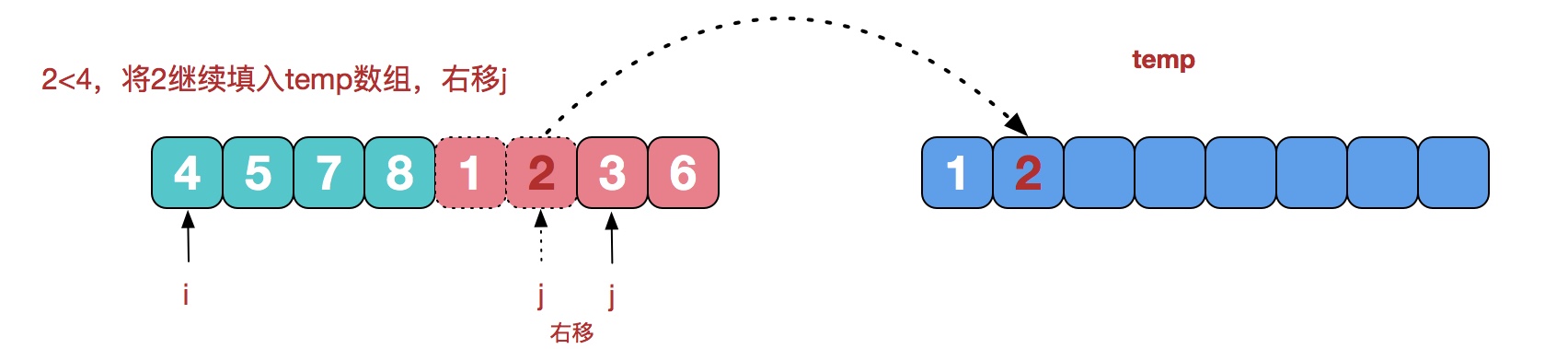
第三步：
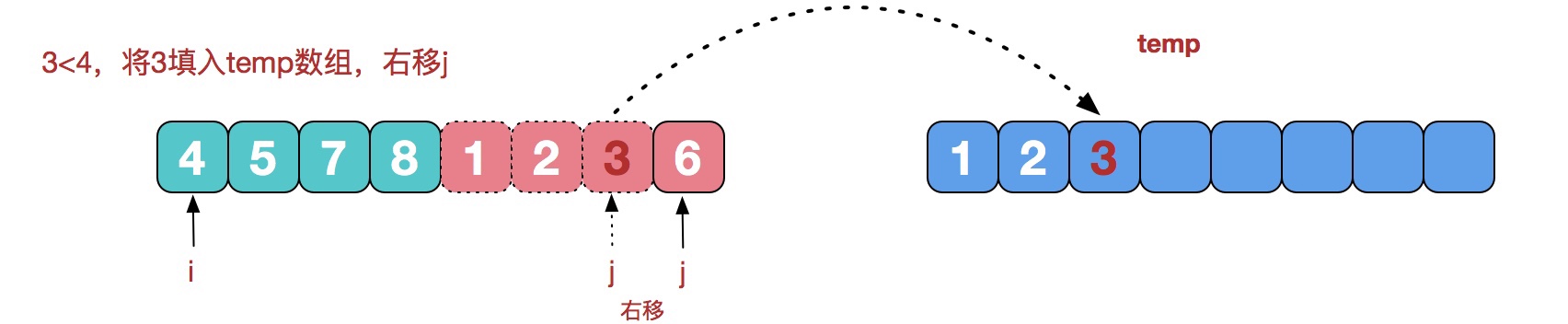
第四步：
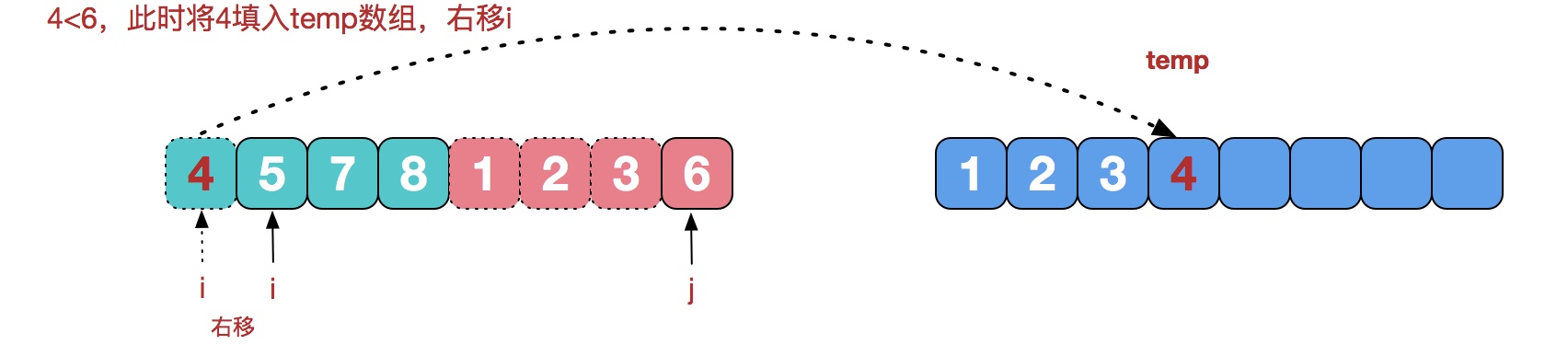
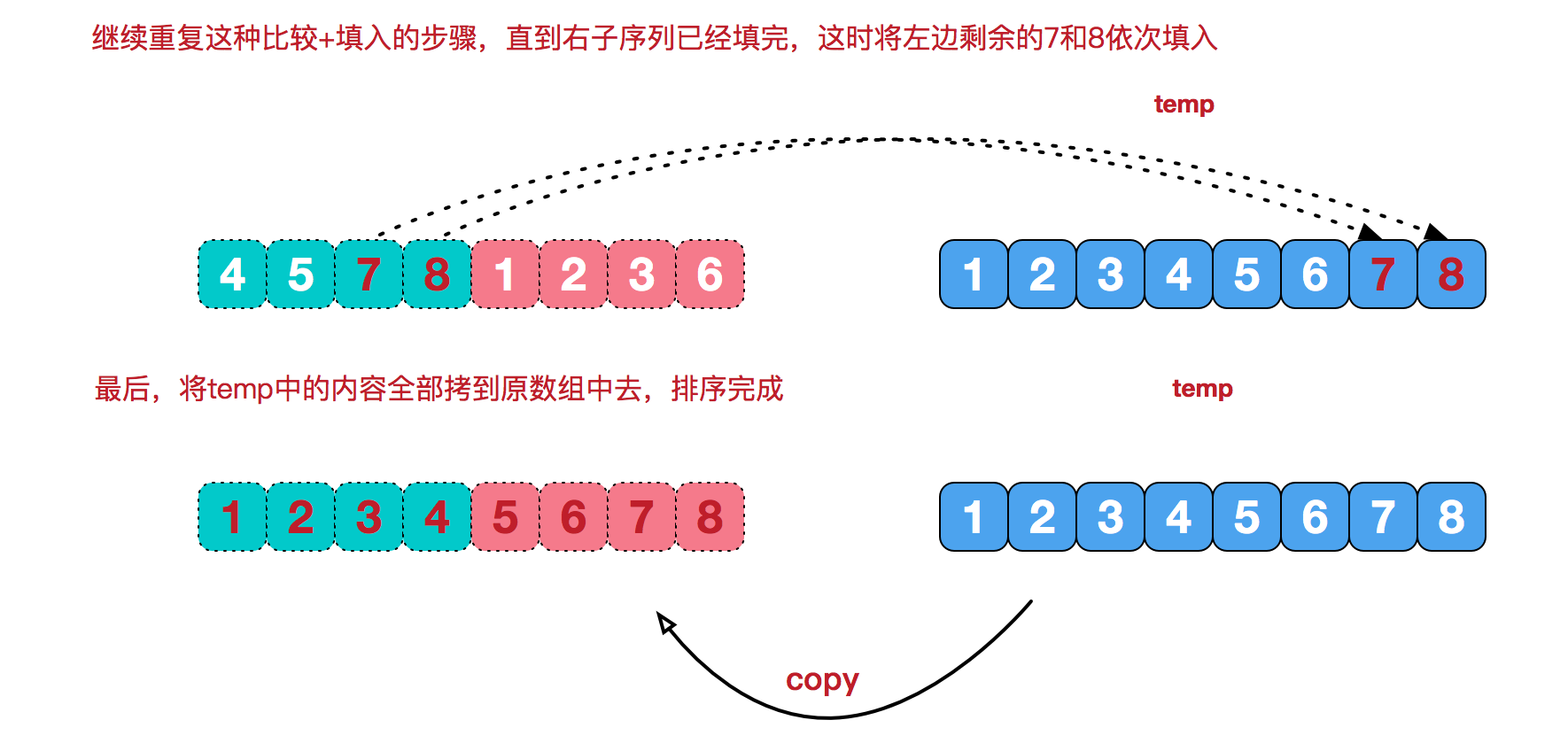
最后这步复制可以依靠memcpy完成
这个循环在终止条件为 两个子序列完全遍历结束，但是事实上实现起来的话，应该是一个子序列遍历完毕后立即退出，再写一个循环，把没有遍历完毕的子序列全部直接填入临时数组。
所以呢这块 “治” 的代码因该是这样子的
1 void mergeAdd(int arr[], int left, int mid, int right, int *temp) 2 { 3 //实现“治” 4 int i = left; 5 int j = mid + 1; 6 int k = left; //临时下标,用于将arr索引映射到temp上 7 while (i <= mid && j <= right) 8 { 9 //选出小的存入temp 10 temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++]; 11 } 12 while (i <= mid) 13 { 14 temp[k++] = arr[i++]; 15 } 16 while (j <= right) 17 { 18 temp[k++] = arr[j++]; 19 } 20 //把temp中的内容拷给arr数组中 21 //进行归并的时候，处理的区间是arr[left,right),对应的会把 22 //这部分区间的数组填到tmp[left,right)区间上 23 memcpy(arr + left, temp + left, sizeof(int) * (right - left + 1)); 24 }
完整的归并排序代码
1 void mergeAdd(int arr[], int left, int mid, int right, int *temp) 2 { 3 //实现“治” 4 int i = left; 5 int j = mid + 1; 6 int k = left; //临时下标,用于将arr索引映射到temp上 7 while (i <= mid && j <= right) 8 { 9 //选出小的存入temp 10 temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++]; 11 } 12 while (i <= mid) 13 { 14 temp[k++] = arr[i++]; 15 } 16 while (j <= right) 17 { 18 temp[k++] = arr[j++]; 19 } 20 //把temp中的内容拷给arr数组中 21 //进行归并的时候，处理的区间是arr[left,right),对应的会把 22 //这部分区间的数组填到tmp[left,right)区间上 23 memcpy(arr + left, temp + left, sizeof(int) * (right - left + 1)); 24 } 25 26 void mergeSort(int arr[], int left, int right, int *temp) 27 { //实现“分” 28 if (left >= right) 29 { //停止条件 30 return; 31 } 32 33 int mid = left + (right - left) / 2; 34 mergeSort(arr, left, mid, temp); 35 mergeSort(arr, mid + 1, right, temp); 36 mergeAdd(arr, left, mid, right, temp); 37 } 38 39 //作为接口函数 40 void MergeSorted(int arr[], int n) 41 { 42 int *temp = malloc(sizeof(int) * n); 43 mergeSort(arr, 0, n - 1, temp); 44 free(temp); 45 }
测试代码：
1 void MergeSorted(int arr[], int n); 2 void ArrayPrint(int arr[], int n); 3 4 int main(void) 5 { 6 int arr[] = {5, 6, 7, 334, 8, 2, 32, 4, 1, 0, 2}; 7 8 MergeSorted(arr, sizeof(arr) / sizeof(arr[0])); 9 ArrayPrint(arr, sizeof(arr) / sizeof(arr[0])); 10 11 return 0; 12 } 13 14 void ArrayPrint(int arr[], int n) 15 { 16 for (int i = 0; i < n; i++) 17 { 18 printf("%d ", arr[i]); 19 } 20 }
到这里归并排序就算讲完了，至于归并排序的非递归实现我就不详细讲了，精心设计以下两个循环的步长就可以轻松完成，再不行用栈呗(*/ω＼*)，直接贴代码了
1 void MergeAdd(int arr[], int left, int mid, int right, int *tmp) 2 { 3 int i = left; 4 int j = mid + 1; 5 int k = left; 6 7 //跑完一个子序列就退出 8 while (i <= mid && j <= right) 9 { 10 tmp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++]; 11 } 12 13 //跑完余下的子序列 14 while (i <= mid) 15 { 16 tmp[k++] = arr[i++]; 17 } 18 while (j <= right) 19 { 20 tmp[k++] = arr[j++]; 21 } 22 23 memcpy(arr + left, tmp + left, sizeof(int) * (right - left + 1)); 24 } 25 26 void MergeSort(int arr[], int len, int *tmp) 27 { 28 if (len <= 1) 29 { 30 return; 31 } 32 33 //定义一个步长gap，初始值为1，相当于每次只合并两个长度为1的元素 34 for (int gap = 1; gap <= len; gap *= 2) 35 { 36 for (int i = 0; i <= len; i += 2 * gap) 37 {//每次的步长都会变1，2，4……（每次写这个就感觉超像希尔排序） 38 int beg = i; 39 int mid = (gap - 1) + i; 40 if (mid >= len) 41 { 42 mid = len; 43 } 44 int end = mid + gap; 45 if (end >= len) 46 { 47 end = len; 48 } 49 MergeAdd(arr, beg, mid, end, tmp); 50 } 51 } 52 } 53 54 void MergeSorted(int arr[], int n) 55 { 56 int *temp = malloc(sizeof(int) * n); 57 MergeSort(arr, n - 1, temp); 58 free(temp); 59 }
算法不易，诸君共勉！
