找出素数
是不是很经典，还记得什么是素数吗。不记得，没事，我不讲。连接在这自己转跳 (●ˇ∀ˇ●)。我比较懒。看完之后让我们来思考一下如何求素数，
首先回顾一下素数的定义：
质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。
由这一条限制可得出一个结论：
存在一个数n，若n被[2,n-1]内的任何一个数整除，那么，这个数就是不是素数。
OK， 根据这个结论我们可以写出最最最暴力的算法，代码如下
1 /** 2 * @brief 素数基本求法 3 * @note 4 * @param num: 被判断的数 5 * @author 杨文蓁的小迷弟 6 */ 7 int IsPrime(int num) 8 { 9 if (num < 2) 10 { 11 return 0; 12 } 13 14 for (int i = 2; i < num; i++) 15 { 16 if (num % i == 0) 17 { 18 19 return 0;20 } 21 } 22 return 1; 23 }
素数判定还有另一种方法：设存在任意一个数m。
如果 m 不能被 2 ~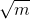 
间任一整数整除，m 必定是素数。
原因如下：
若 m 能被 2 ~ m-1 之间任一整数整除，其两个因子必定有一个小于或等于 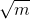，另一个大于或等于 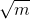。例如 16 能被 2、4、8 整除，16=2*8，2 小于 4，8 大于 4，16=4*4，4=√16，因此只需判定在 2~4 之间有无因子即可。
所以可以写出相应的代码
1 /** 2 * @brief sqrt求素数 3 * @note 离散数学初等数论里有定理 4 * @param num: 要判断的数 5 * @author 杨文蓁小迷弟 6 */ 7 int IsPrime(int num) 8 { 9 if (num < 2) 10 { 11 return 0; 12 } 13 14 int k = (int)sqrt((double)num); 15 for (int i = 2; i <= k; i++) 16 { 17 if (num % i == 0) 18 { 19 20 return 021 } 22 } 23 return 1; 24 }
我一直觉得O（√N）这种时间复杂度已经低了。但是直到我看到一篇博客，我才知道我错了，让我们一起学习一下大佬的思路：
先看一个质数分布的规律：
大于等于5的质数一定和6的倍数相邻。
例如5和7，11和13,17和19等等；
接着我们来证明一下：
证明：令x≥1，将大于等于5的自然数表示如下：
······ 6x-1，6x，6x+1，6x+2，6x+3，6x+4，6x+5，6(x+1），6(x+1)+1 ······
可以看到，不在6的倍数两侧，即 6x 两侧的数为
6x+2，6x+3，6x+4，
由于 2(3x+1)，3(2x+1)，2(3x+2)，所以它们一定不是素数，再除去6x本身，显然，素数要出现只可能出现在6x的相邻两侧。
这里要注意的一点是，在6的倍数相邻两侧并不是一定就是质数。
此时判断质数可以6个为单元快进，原本为1的步长加大为6，加快判断速度。
原因如下：
设要判定的数为n，则n必定是6x-1或6x+1的形式，对于循环中6i-1，6i，6i+1,6i+2，6i+3，6i+4
1、如果n能被6i，6i+2，6i+4整除，则n至少得是一个偶数，但是6x-1或6x+1的形式明显是一个奇数，故不成立；
2、如果n能被6i+3整除，则n至少能被3整除，但是6x能被3整除，故6x-1或6x+1（即n）不可能被3整除，故不成立。
综上，循环中只需要考虑6i-1和6i+1的情况，即循环的步长可以定为6。
呼~，大佬就是大佬望尘莫及。下面贴一下代码：
1 /** 2 * @brief O(((n^(1/2))/3) 3 * @note ozr,膜拜一下大佬的思想。 4 * @param num: 待测数据 5 * @author 杨文蓁的小迷弟 6 */ 7 int IsPrime(int num) 8 { 9 // 0, 1特判 10 if (num < 2) 11 { 12 return 0; 13 } 14 //两个较小数另外处理 15 if (num == 2 || num == 3) 16 { 17 return 1; 18 } 19 20 //不在6的倍数两侧的一定不是质数 21 if (num % 6 != 1 && num % 6 != 5) 22 { 23 return 0; 24 } 25 26 int tmp = sqrt(num); 27 //在6的倍数两侧的也可能不是质数 28 for (int i = 5; i <= tmp; i += 6) 29 { 30 if (num % i == 0 || num % (i + 2) == 0) 31 { 32 return 0; 33 } 34 } 35 //排除所有，剩余的是质数 36 return 1; 37 }
再次膜拜 ozr， ozr
以上的方法应用于素数判断。
接着讲快速打出2~n的素数表：
首先得提的就是埃氏筛法，什么是埃氏筛法？离散数学最后面的基本数论对其思想进行了大致的说明。
思路大致如下：
对于不超过N的素数p，删除2*p,3*p,4*p…，当处理完所有的数之后，还没有被删除的数就都是素数。
代码顺着这个思路写下去就行了。
1 /** 2 * @brief 埃氏筛法 3 * @note 偷懒不用memset，默认0为素数 4 * @param size: 要计算的范围大小 5 * @author 杨文蓁的小迷弟 6 */ 7 int make_prime(int size) 8 { 9 Isprime[0] = 1; 10 Isprime[1] = 1; 11 int cnt = 0; 12 for (int i = 2; i < size; i++) 13 { 14 if (!Isprime[i]) 15 { 16 for (int k = i * i; k < size; k += i) 17 { 18 Isprime[k] = 1; 19 } 20 } 21 } 22 }
解释一下 j = i * i：
因为2*i, 3*i, 4*i, … , (i-1)*i 肯定已经被前面的2, 3, 4, … , (i-1) 这些里面的质数筛掉了。换句话说，我们筛掉的是素数的倍数，那么i的倍数中包括2, 3, … i, …, m，但是比i小的那些倍数，2, 3, … i-1，在i作为素数开始筛合数之前肯定已经i被当作2, 3, … i-1这些中素数的倍数被筛掉了，所以我们只需要从j=i*i 开始即可。
但即使是这样埃氏筛法还是存在重复计算 例如 ，计算 50 以内素数时，在 i = 2，3，5 时，都计算了 30。为了解决这个问题，我们的更厉害的筛法——欧拉筛法（线性筛）就诞生了。
欧拉筛法的思路还是一样的，所以先贴代码。
1 /** 2 * @brief Euler筛法 3 * @note 12 4 * @param size: 范围 5 * @author 杨文蓁的小迷弟 6 */ 7 int Isprime[MAXN]; 8 int Prime[MAXN];//记录素数 9 void Euler_prime(int size) 10 { 11 int cnt = 0;//记录素数个数 12 13 Isprime[0] = Isprime[1] = 1; 14 for (int i = 2; i <= MAXN; i++) 15 { 16 if (!Isprime[i])// 17 { 18 Prime[cnt++] = i; 19 } 20 for (int j = 0; j < cnt && i * Prime[j] < MAXN; j++)//在MAXN范围内讲所有已得出的素数的倍数都清除 21 { 22 Isprime[i * Prime[j]] = 1; 23 if (!(i % Prime[j]))//如果被1某个素数整除的话那就意味着被其他素数筛过了，往后就不用继续了 24 { 25 break; 26 } 27 } 28 } 29 }
讲解一下（虽然我觉得注释已经够详细了），if (!(i % Prime[j]))，这里用到了离散数学(真是好书）里书里的基本数论的 算数基本定理：
一个合数可以被分解为限个质数的乘积
无论 i 是否为素数，都会执行到20行，
1、如果 i 都是是素数的话，
一个大的素数 i 乘以不大于 i 的素数P，这样筛除的数跟之前的是不会重复的。
筛出的数都是 N=P1*P2的形式, P1，P2之间不相等
2、如果 i 是合数，
此时 i 可以表示成递增素数相乘 i = P1*P2*...*Pn, Pi都是素数（2<=i<=n）， pi<=pj ( i<=j )P1是最小的系数。
根据 23行 的退出定义，当P1==prime[j] 的时候，筛除就终止了，也就是说，只能筛出不大于P1的质数*i构成的合数。
我们可以直观地举个例子。
i = 2 * 3 * 5
此时能筛除 2*i ,不能筛除 3*i。
如果能筛除3*i 的话，当 i 等于 i=3*3*5 时，筛除2*i 就和前面重复了
其实就是素数越小筛出范围越大，导致后面的比它大的素数进行了重复筛除，为了减小重复所以对小素数的筛除范围进行了限制。
目前我的能力只能写到这种程度了，正在学素数定理，后期应该会继续更。
算法不易，诸君共勉！
