数据结构——KMP(串)
KMP一个非常经典的字符串模式匹配算法,虽然网上有很多kmp算法的博客,但是为了更好的理解kmp我还是自己写了一遍(这个kmp的字符串存储是基于堆的(heap),和老师说的定长存储略有不同,字符串索引从0开始)
先来说说 KMP 的历史吧。
一、背景
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度度O(m+n)。KMP也可以处理最重复长子串问题,最长子串问题……这里挂一道最简单的题leetcode的 实现 strStr(),大家看完可以去试一试。
补充说明:
强调两个概念:真前缀 ,真后缀

如图所示,所谓的真前缀,就是在指在除了自身之外的全部字符串的头部顺序组合;而"真后缀",就是指在除自身之外的一个字符串的全部尾串的顺序组合 。与后缀、前缀不同:
真前/后缀不包含自身字符!!!
其实就类似于离散数学中集合里子集与真子集的概念。
二、朴素字符串匹配算法
其实就是我们最开始的时候写的字符串匹配,就是两个字符串逐一匹配。不作详细介绍,代码如下
/** * @brief 朴素字符串匹配 * @note * @param MainString: 主串 * @param Pattern: 模式串 * @retval */ int SimpleStringMatch(char* MainString, char* Pattern) { int i = 0; int j = 0; int PatternLen = strlen(Pattern); int MainStringLen = strlen(MainString); while (i < MainStringLen && j < PatternLen) { if (S[i] == Pattern[j]) { i++; j++; } else { i = i - j + 1; j = 0; } } if (j == PatternLen) { return i - j; } return -1; }
很显然暴力匹配的时间复杂度为O(m*n)。m,n 分别取决于MainString和Pattern的长度,很显然这种时间复杂度还很高的。这个算法一旦匹配失败就主串索引 +1 ,模式串索引重置,当主串为 ABCDEABCDEF 模式串为 ABCDEF 。啊,完美体现了暴力匹配的缺点——逐一匹配(管你之前比没比过)。当你 A != F 时,我们人肯定会从第二个A处继续查找,让余下的部分和模式串继续进行匹配。如果计算机这样执行,那么算法的时间复杂度就从O(m*n)降到了O(m+n)从乘数级算法瞬间降到了无限接近常数级的算法,神优化啊(再次膜拜大神)。但是计算机不会啊,他只会勤勤恳恳的执行我们所写的代码,因此它就会从第一个B处开始比较,但是事实上从 B ~ E 的所有匹配都是无用功,为了解决这个问题 KMP应运而生。
三、KMP字符串模式匹配算法
3.1 算法流程:
(1)
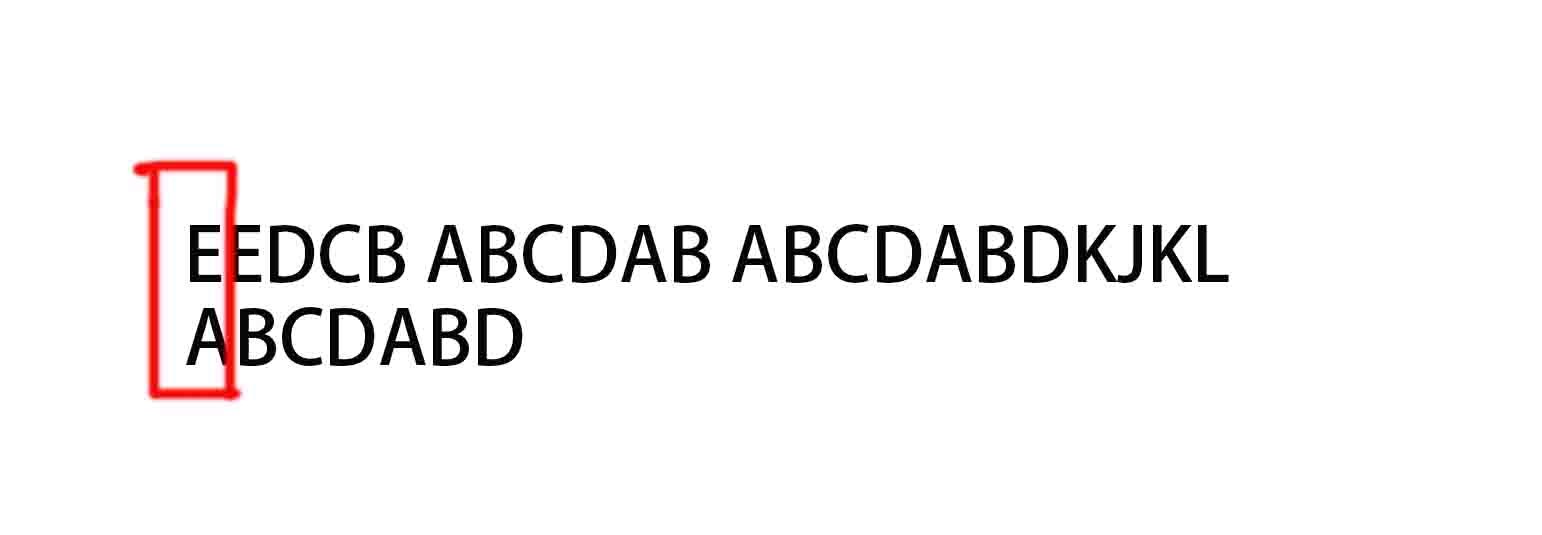
第一步 主串"E……" 与 模式串 "ABCDABD" 的第一个字符进行比较。‘E!= ’A,模式串索引不变,主串索引+1
(2)

E与A仍然不匹配,继续后移知道第一个匹配的位置
(3)
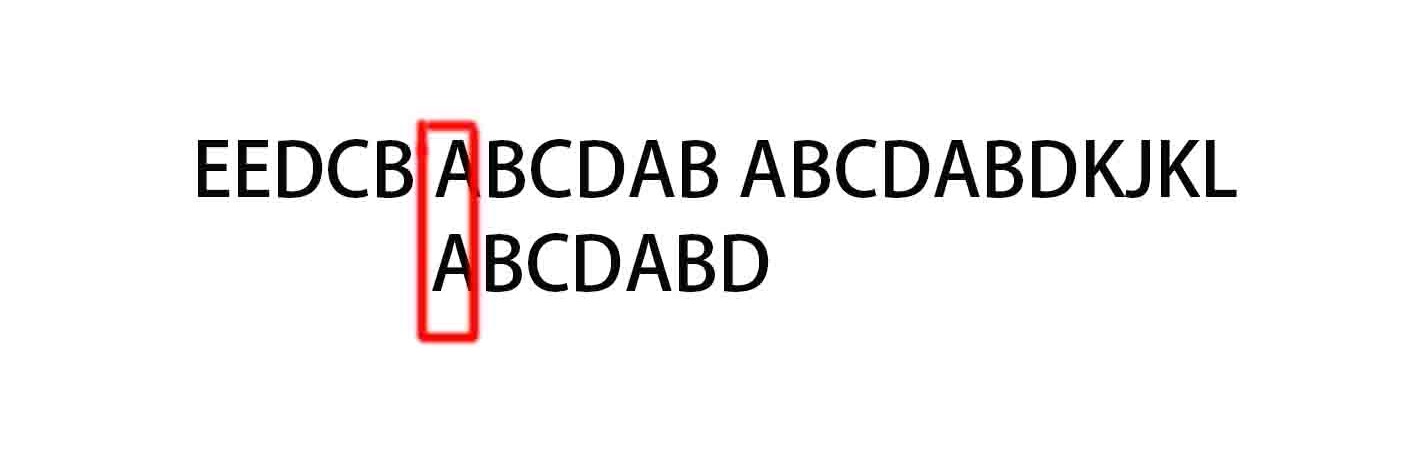
抵达第一处相同点
(4)

第二处相同点,继续
(5)

嗯!,不匹配了,怎么办呢。
(6)

第一反应肯定是把模式串整体后移一位然后重新一位位的比较,这样子是没有问题,但是这就不是kmp了,没有利用已完成的匹配信息。
(7)

当我们发现D和空格不匹配的时候,我们已经知道了前面6个字符为ABCDAB(主串)。KMP就是充分利用了这个信息。将模式串继续后移,没有将其移回比较过的位置。
(8)
计算机不比我们大脑,这种的事情对它来说已经很困难了,肯定要给它写个专门的算法了。KMP的索引的转跳依赖的是next[] 数组。如图,我们先用,先对KMP有一个完整的理解再来进行实现。理解才是关键。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | C | D | A | B | D | '\0' |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1· | 2 | 0 |
(9)

如图,D与空格不匹配,D之前的字符已经完成匹配,为已知信息。根据转跳数组可知,不匹配出D的next值为2,因此接下来从模式串所引为2的位置进行匹配。
(10)
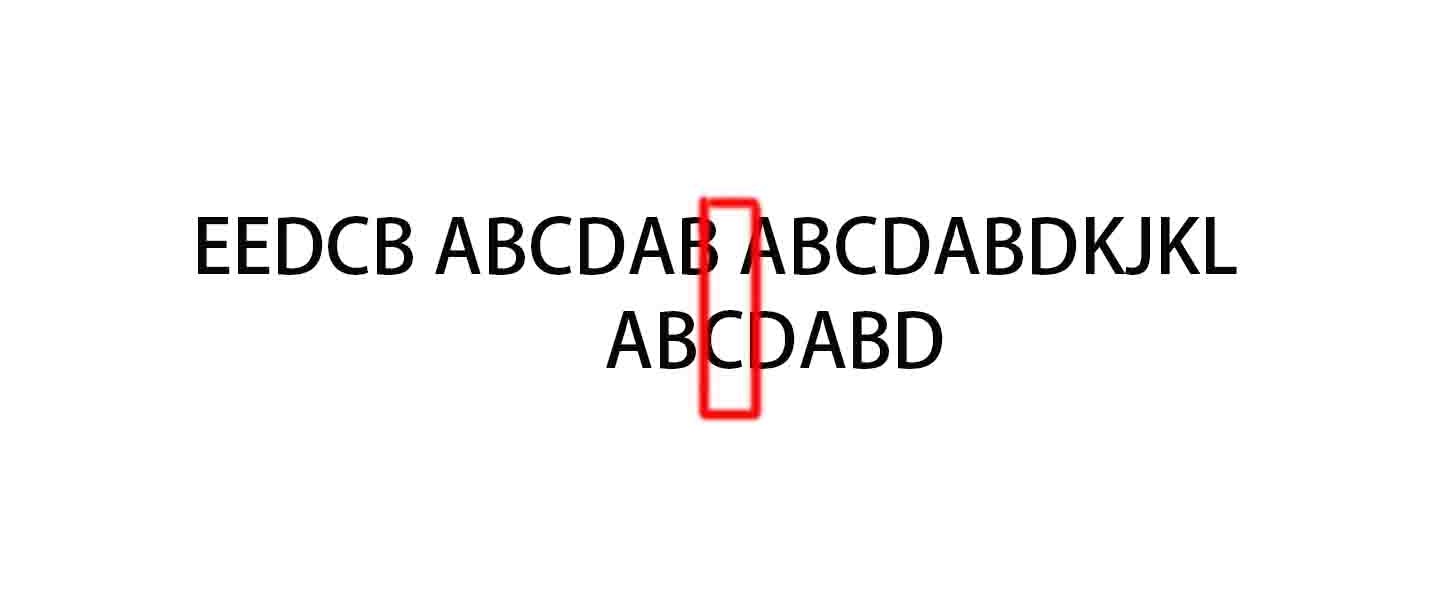
同样的,C与空格不匹配,C处的next为0,所以下一个从索引为0的位置进行匹配。
(11)

A与空格比较不匹配,此处next值为-1,表示模式串的索引为1字符就不匹配,那么直接往后移一位。
(12)

一位位的比较直到完全匹配。
其实KMP的比较算法和朴素匹配的方法是一样的,KMP之所以快是快在索引的转跳上。接着我们就来说一下next数组是u如何实现的。
3.2 next数组实现:
next数组的求解基于 "真前缀" 和 "真后缀" ,即next[i]等于P[0]...P[i - 1]最长的相同真前后缀的长度。(忘记的赶紧上去看看,要不然会一直懵的)。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | C | D | A | B | D | '\0' |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1· | 2 | 0 |
- i = 0,对于模式串的首字符,我们统一为next[0] = -1;
- i = 1,前面的字符串为A,其最长相同真前后缀长度为0,即next[1] = 0;
- i = 2,前面的字符串为AB,其最长相同真前后缀长度为0,即next[2] = 0;
- i = 3,前面的字符串为ABC,其最长相同真前后缀长度为0,即next[3] = 0;
- i = 4,前面的字符串为ABCD,其最长相同真前后缀长度为0,即next[4] = 0;
- i = 5,前面的字符串为ABCDA,其最长相同真前后缀为字符A,即next[5] = 1;
- i = 6,前面的字符串为ABCDAB,其最长相同真前后缀为字符AB,即next[6] = 2;
- i = 7,前面的字符串为ABCDABD,其最长相同真前后缀长度为0,即next[7] = 0。
那么,这个数组是如何实现不匹配自动跳转的呢?
举个栗子:前置字符串
假如 i = 6 时不匹配,其前置字符串为 “ABCDAB”,仔细观察,首尾都有 “AB”,这意味着主串和模式串刚刚比较完 “AB”。那,当进行下一次比较的时候,我们就可以直接用 i = 2 时的字符C进行下一次匹配。因为刚刚模式串后方的“AB”刚比较完,所以没有必要再进行。i = 6 时候字符D的其最长相同真前后缀为字符恰好也为“AB”,长度恰好等于索引,刚好能转跳到C。
但是现在有一个问题,看表中 i = 5 时,匹配失败, next数组值为1,这不符KMP的理念啊。理论上,我们应该把 i = 2 处的字符拿过来匹配,如果拿 i = 1 处的字符那就会产生一次多余的比较。这个问题的遗留并不是算法问题,而是算法没有优化,KMP未优化的算法是用也是有特定作用的。两种算法应用场景不同,各有所长。(最后会说明优化算法的)。
下面是代码实现:
/** * @brief next[] * @note 未优化KMP,j == -1 不可删除 * @param Pattern: 模式串 * @param next[]: 转跳数组 * @retval None */ void GetNext(char* Pattern, int next[]) { int Pattern_len = strlen(Pattern); int i = 0; // Pattern 的下标 int j = -1; next[0] = -1; while (i < Pattern_len - 1) { if (j == -1 || Pattern[i] == Pattern[j]) { i++; j++; next[i] = j;//匹配就递推 } else { j = next[j];//不匹配就转跳到上一个匹配的位置 } } }
有没有看懂的,我觉得肯定有。有我也得分析一下这个算法干了什么。
其实,这个代码最难理解的就在于 if……else……
先上张图(感谢大佬给我的图)
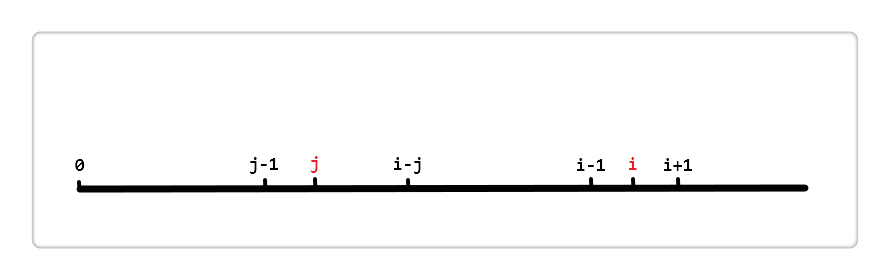
现在我假设 i 和 j 的位置如上,由前面代码中的 next[i] = j 得, i 的最长相同真前后缀分别是 [0, j-1] 和 [i-j, i-1],即这两段内容相同
走流程:
if (j == -1 || Pattern[i] == Pattern[j]) {
i++; j++; next[i] = j; } else {
j = next[j]; }
next[j] 表 [0,j - 1] 区间中最长相同真前后缀的长度。如图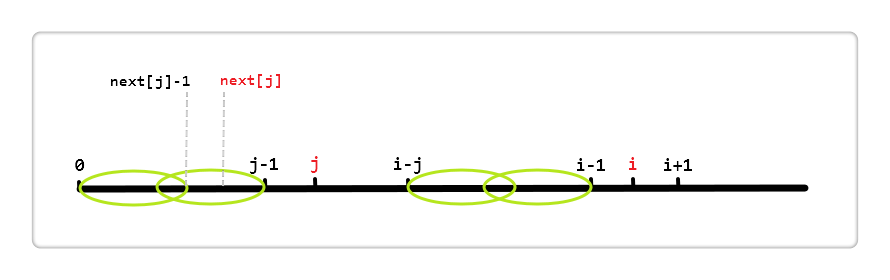
左侧两个椭圆来表示这个最长相同真前后缀,即这两个椭圆代表的区段内容相同;同理,右侧也有相同的两个椭圆。所以else语句就是利用第一个椭圆和第四个椭圆内容相同来加快得到[0, i - 1]区段的相同真前后缀的长度。说到在透彻一些就是 j = next[j],这句语句减少了无用的比较。
有没有想过,为什么next的第一个值为-1呢?
第一,
程序刚运行时,j是被初始为-1,直接进行 Pattern[i] == Pattern[j] 判断无疑会边界溢出;
第二,
else语句中j = next[j],j 是不断后退的,若 j 在后退中被赋值为 -1(也就是 j = next[0]),在 Pattern[i] == Pattern[j] 判断也会边界溢出。
综上,其意义就是为了特殊边界判断,而且 j 一开始被赋值为-1,比较方便给第二项赋值。
四、KMP样例实现
最好自己实现一遍!!!

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 5 int KMP(char* MainString, char* Pattern); 6 void GetNext(char* Pattern, int next[]); 7 8 int main() 9 { 10 printf("%d\n",KMP("ljhgfdsa asdfghjkl\0", "dfghj\0")); 11 } 12 13 int KMP(char* MainString, char* Pattern) 14 { 15 int next[22400] = {0}; 16 GetNext(Pattern, next); 17 18 int i = 0; 19 int j = 0; 20 int s_len = strlen(MainString); 21 int PatternLen = strlen(Pattern); 22 23 while (i < s_len && j < PatternLen) 24 { 25 if (j == -1 || MainString[i] == Pattern[j]) 26 { 27 i++; 28 j++; 29 } 30 else 31 { 32 j = next[j]; 33 } 34 } 35 36 if (j == PatternLen) 37 { 38 return i - j; 39 } 40 41 return -1; 42 } 43 44 void GetNext(char* Pattern, int next[]) 45 { 46 int PatternLen = strlen(Pattern); 47 int i = 0; 48 int j = -1; 49 next[0] = -1; 50 51 while (i < PatternLen - 1) 52 { 53 if (j == -1 || Pattern[i] == Pattern[j]) 54 { 55 i++; 56 j++; 57 next[i] = j; 58 } 59 else 60 { 61 j = next[j]; 62 } 63 } 64 }
五、KMP优化
还记得上面的那个问题吗?KMP不够完美的问题,其实只需要判断一下他们是不是相等的字符,然后进行处理即可。
处理方式:获取前一个字符的最长字串。
自己先试试

void GetNextval(char *Pattern, int nextval[]) { int p_len = strlen(Pattern); int i = 0; int j = -1; nextval[0] = -1; while (i < p_len - 1) { if (j == -1 || Pattern[i] == Pattern[j]) { i++; j++; //优化 if (Pattern[i] != Pattern[j]) { nextval[i] = j; } else { nextval[i] = nextval[j]; \\一样的时候最长字串来源于前一个 } } else { j = nextval[j]; } } }
KMP算法(未优化版): next数组表示最长的相同真前后缀的长度,我们不仅可以利用next来解决模式串的匹配问题,也可以用来解决类似字符串重复问题等等,这类问题大家可以在各大OJ找到。
KMP算法(优化版): 根据代码很容易知道(名称也改为了nextval),优化后的next仅仅表示相同真前后缀的长度,但不一定是最长(称其为“最优相同真前后缀”更为恰当)。此时我们利用优化后的next可以在模式串匹配问题中以更快的速度得到我们的答案(相较于未优化版),但是上述所说的字符串重复问题,优化版本则束手无策。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号