leetcode 542 01 Matrix, 01矩阵 JavaScript解法

题目描述：

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

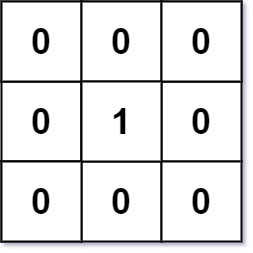
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

给定一个二维数组组成的矩阵，需要返回 每个格子距离最近0的步数 组成的二维数组。

思路：
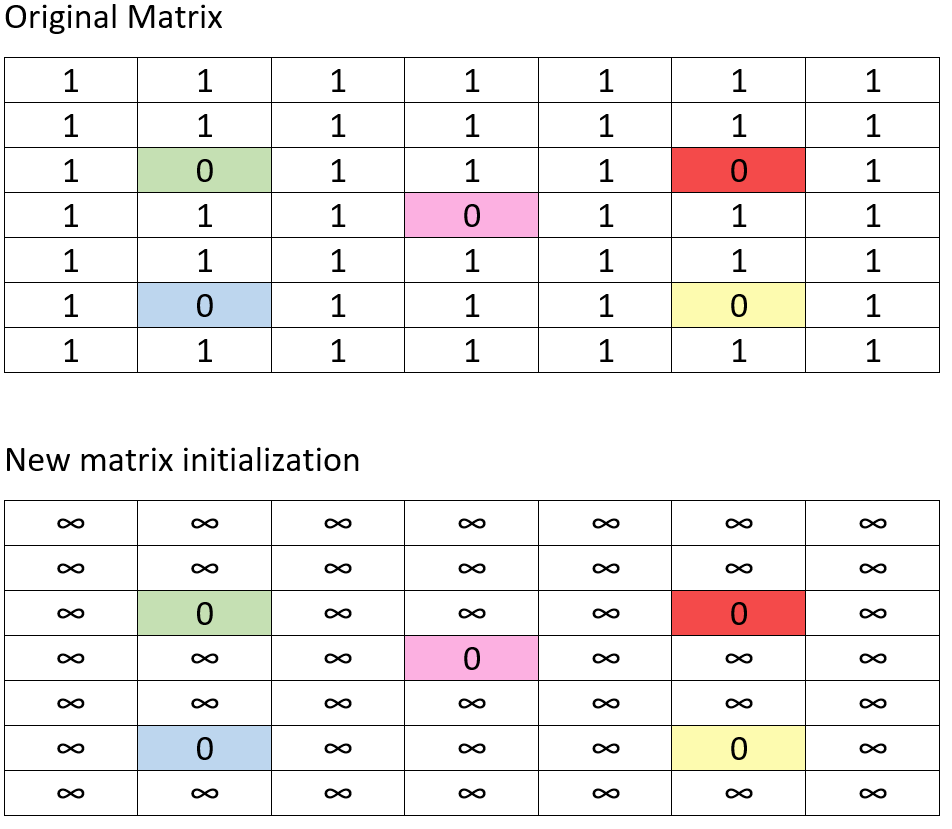
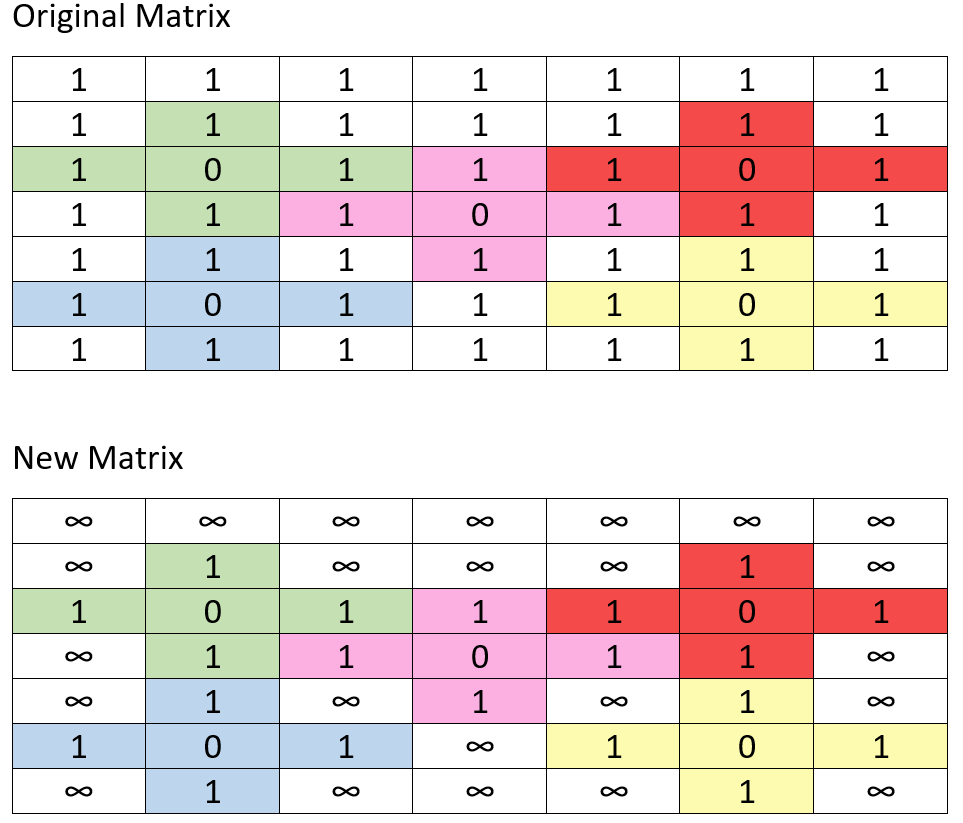
可以确定的是，如果当前格子中的数字是0，那么它对应的返回值就是0，可以从已经的0入手，辐射四周，找出最近的1，即可计算出1需要的步数。leetcode上有位大神给出了这几张图，
可以看出整个查找的过程。

第一步：初始化返回二维数组，把当前是0的格子，用0填充，其他用Infinity 无穷大填充

 

 用BFS循环查找

步数为1步的，设值

 

 

 步数：2步

 

 

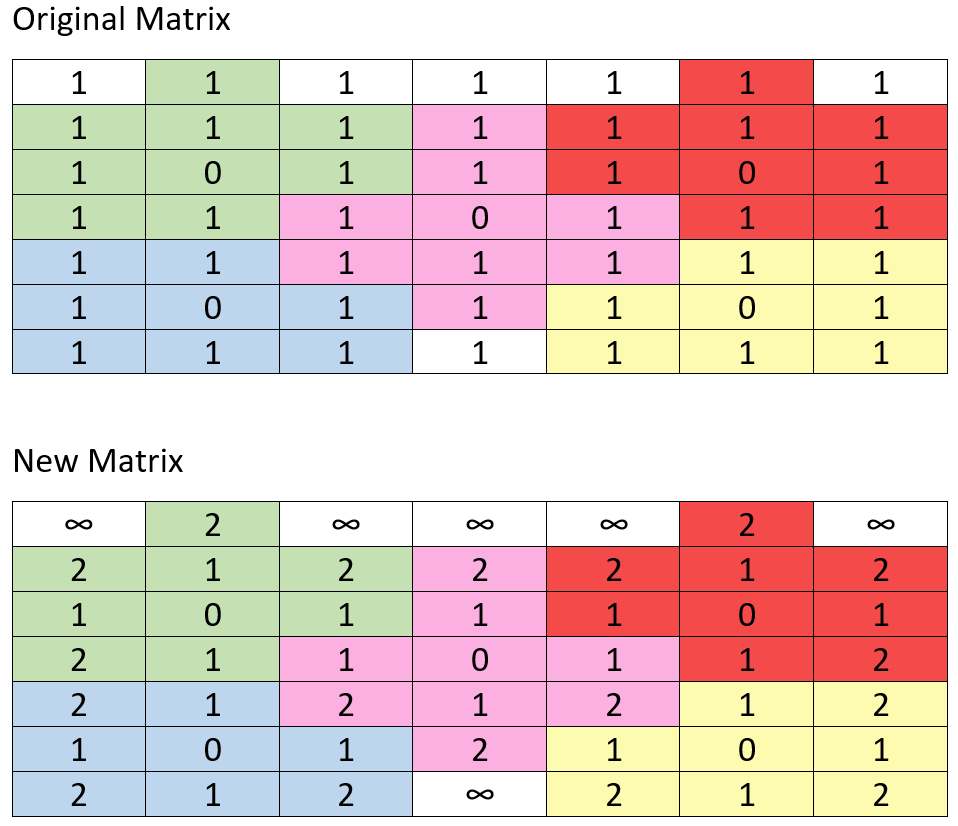
 步数3步

 完成了BFS循环，队列为空，已经找出所有的格子步数，返回结果即可。

用代码来表示一下：

var updateMatrix = function(mat) {
        if(!mat.length)  return [];

        let ret = [];
        let m = mat.length;
        let n = mat[0].length;
        let queue = [];
        let directions = [[1,0],[-1,0],[0, 1],[0, -1]]; //上下左右四个格子
        
        //初始化ret返回值，把当前为0的格子，值设置为0，并放入队列中，当前为1的格子值初始化为无穷大
        for(let x = 0; x < m; x++){
            for(let y=0; y< n; y++){
                ret[x] = ret[x]?ret[x]:[];
                
                if(mat[x][y] === 0){
                    ret[x][y] = 0;
                    queue.push([x,y]);
                }else{
                     ret[x][y] = Infinity;
                }
            }
        }
       
       //遍历刚刚放入队列中的0，查找它的上下左右中的1(注意不要出界)，找到有1就设置步数，并且把这个1放入队列中，方便第二轮查找的时候用
       while(queue.length){
           let [x,y] = queue.shift();
           directions.forEach(_item =>{
               let [nx,ny] = _item;
               let newx = x + nx;
               let newy = y + ny;
               if(isBound(newx,newy) && ret[newx][newy] > ret[x][y] + 1){
                   ret[newx][newy] = ret[x][y] + 1;
                   queue.push([newx,newy])
               }
           })
           
       }
       
       function isBound(x,y){
           return x>=0 && x < m && y >=0 && y < n
       }
       
        return ret;
    };

 

第二种解法，思想也是类似的，不过代码写起来更好理解

   var updateMatrix = function(mat) {
        if(!mat.length)  return [];

        let ret = [];
        let m = mat.length;
        let n = mat[0].length;
        
        
        //第一步遍历二维数组，如果当前格子是0，就设置为0，否则设置为无穷大
        for(let x = 0; x < m; x++){
            for(let y=0; y< n; y++){
                ret[x] = ret[x]?ret[x]:[];
                
                if(mat[x][y] === 0){
                    ret[x][y] = 0;
                }else{
                     ret[x][y] = Infinity;
                }
                
                //这里会拿当前格子的top和left的格子来比较，为什么 是top和left，因为我 
                //们此次遍历的顺序是从矩阵的左上到右下，这样的话， top和left都是已经遍 
                //历过了的，可能已经拿到了最小步数，这时候只需要在它们最小步数的基础 
                //上加1就可以了

                if(x > 0) ret[x][y] = Math.min(ret[x][y],ret[x -1 ][y] + 1);
                if(y > 0) ret[x][y] = Math.min(ret[x][y],ret[x ][y - 1] + 1)
            }
        }
       
       //第二次遍历，是从矩阵的右下方到左上方，所以可以拿当前格子的右边和下方的格 
        子来比较，同样因为这两个格子都是已经遍历过了的，已经拿到了最小步数，在此基 
        础上+1即可
      for(let x = m - 1; x >= 0; x--){
            for(let y= n - 1; y >= 0; y--){
                
                if(x < m-1) ret[x][y] = Math.min(ret[x][y],ret[x + 1][y] + 1);
                if(y < n-1) ret[x][y] = Math.min(ret[x][y],ret[x ][y + 1] + 1);
               ;
            }
        }

        return ret;
    };

 
如果觉得有用，不妨点个赞哦~