快速求熵程序（续）

这篇blog是对快速求熵程序的数学解释。

首先，还是从熵的计算公式出发，略做一些推导：

$ Entropy=-\sum_{i=1}^{n}P(X_{i})log_{2}P(X_{i})$

$=-\sum_{i=1}^{n}\frac{C(X_{i})}{T}log_{2}\frac{C(X_{i})}{T}$

$=-\frac{1}{T}\sum_{i=1}^{n}C(X_{i})(log_{2}C(X_{i})-log_{2}T)$

$=-\frac{1}{T}(\sum_{i=1}^{n}C(X_{i})log_{2}C(X_{i})-log_{2}T\sum_{i=1}^{n}C(X_{i}))$

$=\frac{1}{T}(Tlog_{2}T-\sum_{i=1}^{n}C(X_{i})log_{2}C(X_{i}))$

 

令 $f(x)=2^{23}xlog_{2}x$，那么，

$ Entropy=\frac{1}{2^{23}T}(f(T)-\sum_{i=1}^{n}f(C(X_{i})))$

 

fast_entropy()的代码，就是上面公式的直接实现，其中_lxlogx()即为公式中的$f(x)$。

double fast_entropy(int *counts, int n, int total)
{
    long long s = 0;
    int i, c;
    for(i = 0; i < n; i++) {
        if(c = counts[i])
            s -= _lxlogx(c);
    }
    s += _lxlogx(total);
    s /= total;
    return 0.00000011920929 * s;
}

 _lxlogx()的代码，只有4行。前3行完成了$2^{23}log_{2}x$的计算，考虑编译后的ASM指令，除了int->float的转换将产生一条FPU的FILD指令外，其余均为整数操作。

static inline long long _lxlogx(int x)
{
    float f = (float)x;
    int i = *(int *)&f;
    i += _u[(i & 0x007F8000) >> 15];
    return (long long)i * x; 
}

 1个float浮点数占用4字节，按IEEE 754标准格式存储。假设有float浮点数$x$，我们把它的4个字节当做1个32-bit的整数读取，得到$I_{x}$，那么存在近似关系：

$2^{23}log_{2}x\approx I_{x}-2^{23}(127-u)$

这个关系的推导过程见这里。其中，$u (u > 0)$是一个自定义的数，它的数值影响近似程度。具体地，$u$的取值应该尽量让下面的近似误差更小：

$log_{2}(1+x)\approx x + u, (0\leq x < 1, u > 0)$

定义误差函数$e(u)=log_{2}(1+x)- (x+u)$，求解：$\int_{0}^{1}e(u)dx=0$

 

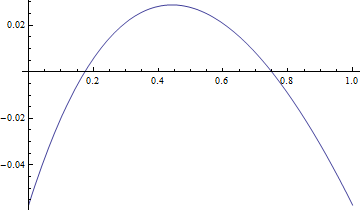
得到$ u^{*}=0.0573049591110366 $。$e(u^{*})$的图像为，

 有没有办法让误差更小呢？可以把$[0,1)$区间分成若干段，为每段找出不同的$u^{*}$。在fast_entropy中，我把$[0,1)$等分成了256个段，对于第 $i (i=0,1,2,...,255)$ 段来说，$u_{i}^{*}$满足：

$\int_{\frac{i}{256}}^{\frac{i+1}{256}}e(u_{i}^{*})dx=0$

计算出256个 $u_{i}^{*}$。

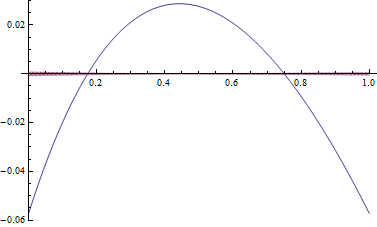
下面图像中，可以看到分段后的误差（紫色）和分段前（蓝色）相比，减小了很多。

这也是fast_entropy中那个_u[256]的来源。当然_u是个32-bit整数数组，每一项是这样计算出来的，

_u[$i$] = $\left [ 2^{32}-2^{23}(127-u_{i}^{*})\right ] $

 

到这里，fast_entropy所有代码的原理已经解释完毕。

_u数组是控制误差的所在，可以通过增加分段数量，即增加数组大小的方法来提高计算精度，而不会对计算效率产生明显影响。对于大多数实际应用，256项的_u的精度已经足够。