dijkstra算法---通过边实现松弛

图片素材借鉴啊哈磊的博客 

该算法用于解决一个点到其余各顶点的最短路径

先来一张图，求1点到6点的最短路径

这让我想起了差点挂科的运筹学

先用一个二维数组

还有一个一维数组存储1点到各点的距离

这个一维数组的值称为估计值。在1点可直接到达的点中选择一个最近的点，即点2.然后点2的值也就成为了确定值。

why。因为路径是正数，也不可能通过其他的中转点缩短点1到点2的路程。

经过了点2，再看看点2能够到达哪些点。即点3和点4。先讨论下通过点2这个中转点是否能够缩短点1到点3的路程。答案是可以的。1+9<12.修改一维数组对应的值。

这个就叫松弛

同理比较点1到点4距离和通过点2中转的距离。

剩下的3，4，5，6点自己试试。不然运筹学很容易挂的

最后答案是

贴出核心算法

  for(i=1;i<=n-1;i++)
    {
        //找到离1号顶点最近的顶点
        min=inf;//初始min为正无穷
        for(j=1;j<=n;j++)
        {
            if(book[j]==0 && dis[j]<min)
            {
                min=dis[j];//取得离源点直接相连的最近的点的距离
                u=j;
            }
        }
        book[u]=1;//将该点纳入已经确定要走的点的集合
        for(v=1;v<=n;v++)//这里就如同遍历哥各点到点2的距离
        {
            if(e[u][v]<inf)
            {
                if(dis[v]>dis[u]+e[u][v]) 
                    dis[v]=dis[u]+e[u][v];
            }
        }    
    }

　　但是这个算法的时间复杂度是0（N^2）.我希望他的时间复杂度降为0（（M+N）logN）

 

4 5

1 4 9

4 3 8

1 2 5

2 4 6

1 3 7

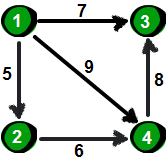
第一行两个整数n,m分别代表点的个数，路线的数量。

接下来的五行x,y,z.代表点x到点y的距离z。

 

存储的结构是这样的。就像hashmap

 

再用一个first数组来存储每个顶点其中一条边的编号。以便待会我们来枚举每个顶点所有的边（你可能会问：存储其中一条边的编号就可以了？不可能吧，每个顶点都需要存储其所有边的编号才行吧！甭着急，继续往下看）。比如1号顶点有一条边是 “1 4 9”（该条边的编号是1），那么就将first[1]的值设为1。如果某个顶点i没有以该顶点为起始点的边，则将first[i]的值设为-1。现在我们来看看具体如何操作，初始状态如下。

咦？上图中怎么多了一个next数组，有什么作用呢？不着急，待会再解释，现在先读入第一条边“1 4 9”。

读入第1条边（1 4 9），将这条边的信息存储到u[1]、v[1]和w[1]中。同时为这条边赋予一个编号，因为这条边是最先读入的，存储在u、v和w数组下标为1的单元格中，因此编号就是1。这条边的起始点是1号顶点，因此将first[1]的值设为1。

另外这条“编号为1的边”是以1号顶点（即u[1]）为起始点的第一条边，所以要将next[1]的值设为-1。也就是说，如果当前这条“编号为i的边”，是我们发现的以u[i]为起始点的第一条边，就将next[i]的值设为-1（貌似的这个next数组很神秘啊⊙_⊙）。

读入第2条边（4 3 8），将这条边的信息存储到u[2]、v[2]和w[2]中，这条边的编号为2。这条边的起始顶点是4号顶点，因此将first[4]的值设为2。另外这条“编号为2的边”是我们发现以4号顶点为起始点的第一条边，所以将next[2]的值设为-1。

读入第3条边（1 2 5），将这条边的信息存储到u[3]、v[3]和w[3]中，这条边的编号为3，起始顶点是1号顶点。我们发现1号顶点已经有一条“编号为1 的边”了，如果此时将first[1]的值设为3，那“编号为1的边”岂不是就丢失了？我有办法，此时只需将next[3]的值设为1即可。现在你知道next数组是用来做什么的吧。next[i]存储的是“编号为i的边”的“前一条边”的编号。

读入第4条边（2 4 6），将这条边的信息存储到u[4]、v[4]和w[4]中，这条边的编号为4，起始顶点是2号顶点，因此将first[2]的值设为4。另外这条“编号为4的边”是我们发现以2号顶点为起始点的第一条边，所以将next[4]的值设为-1。

读入第5条边（1 3 7），将这条边的信息存储到u[5]、v[5]和w[5]中，这条边的编号为5，起始顶点又是1号顶点。此时需要将first[1]的值设为5，并将next[5]的值改为3。

 

核心代码

int n,m,i;
//u、v和w的数组大小要根据实际情况来设置，要比m的最大值要大1
int u[6],v[6],w[6];
//first和next的数组大小要根据实际情况来设置，要比n的最大值要大1
int first[5],next[5];
scanf("%d %d",&n,&m);
//初始化first数组下标1~n的值为-1，表示1~n顶点暂时都没有边
for(i=1;i<=n;i++)
    first[i]=-1;
for(i=1;i<=m;i++)
{
    scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边
    //下面两句是关键啦
    next[i]=first[u[i]];
    first[u[i]]=i;
}