【图像缩放】双立方(三次)卷积插值
前言
图像处理中有三种常用的插值算法:
-
最邻近插值
-
双线性插值
-
双立方(三次卷积)插值
其中效果最好的是双立方(三次卷积)插值,本文介绍它的原理以及使用
如果想先看效果和源码,可以拉到最底部
本文的契机是某次基于canvas做图像处理时,发现canvas自带的缩放功能不尽人意,于是重温了下几种图像插值算法,并整理出来。
为何要进行双立方插值
-
对图像进行插值的目的是为了获取缩小或放大后的图片
-
常用的插值算法中,双立方插值效果最好
-
本文中介绍双立方插值的一些数学理论以及实现
双立方和三次卷积只是这个插值算法的两种不同叫法而已,可以自行推导,会发现最终可以将求值转化为卷积公式
另外,像Photoshop等图像处理软件中也有这三种算法的实现
数学理论
双立方插值计算涉及到16个像素点,如下图
![]()
简单分析如下:
-
其中
P00代表目标插值图中的某像素点(x, y)在原图中最接近的映射点- 譬如映射到原图中的坐标为
(1.1, 1.1),那么P00就是(1, 1)
- 譬如映射到原图中的坐标为
-
而最终插值后的图像中的
(x, y)处的值即为以上16个像素点的权重卷积之和
下图进一步分析
![]()
如下是对图的一些简单分析
-
譬如计算插值图中
(distI, distJ)处像素的值 -
首先计算它映射到原图中的坐标
(i + v, j + u) -
也就是说,卷积计算时,
p00点对应(i, j)坐标 -
最终,
插值后的图中(distI, distJ)坐标点对应的值是原图中(i, j)处邻近16个像素点的权重卷积之和i, j的范围是[i - 1, i + 2],[j - 1, j + 2]
卷积公式
-
设采样公式为
S(x) -
原图中每一个
(i, j)坐标点的值得表达式为f(i, j) -
插值后对应坐标的值为
F(i + v, j + u)(这个值会作为(distI, distJ)坐标点的值)
那么公式为:
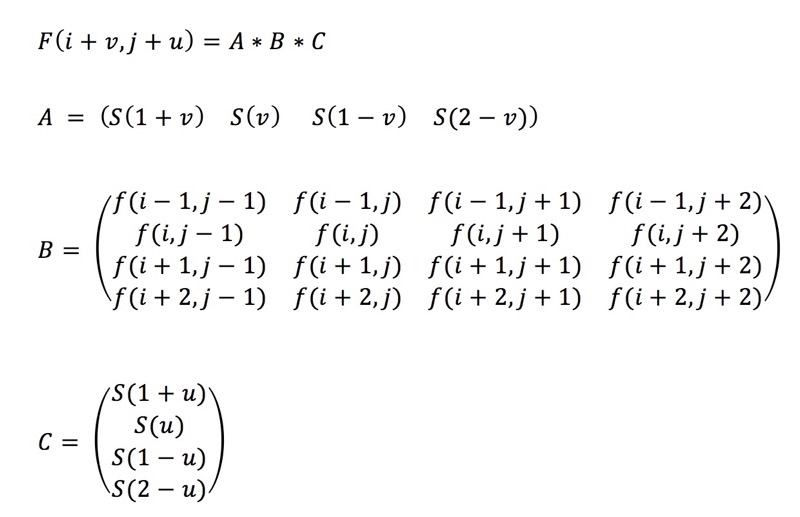
等价于(可自行推导)
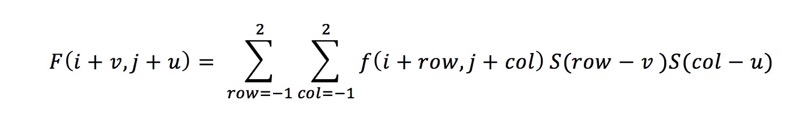
提示
一定要区分本文中v, u和row, col的对应关系,v代表行数偏差,u代表列数偏差(如果混淆了,会造成最终的图像偏差很大)
如何理解卷积?
这是大学数学内容,推荐看看这个答案如何通俗易懂的解释卷积-知乎
采样公式
在卷积公式中有一个S(x),它就是关键的卷积插值公式
不同的公式,插值效果会有所差异(会导致加权值不一样)
本文中采用WIKI-Bicubic interpolation中给出的插值公式:
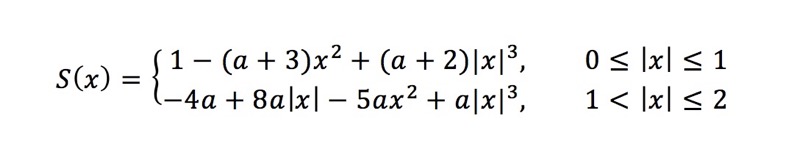
公式中的特点是:
-
S(0) = 1 -
S(n) = 0(当n为整数时) -
当x超出范围时,S(x)为0 -
当
a取不同值时可以用来逼近不同的样条函数(常用值-0.5, -0.75)
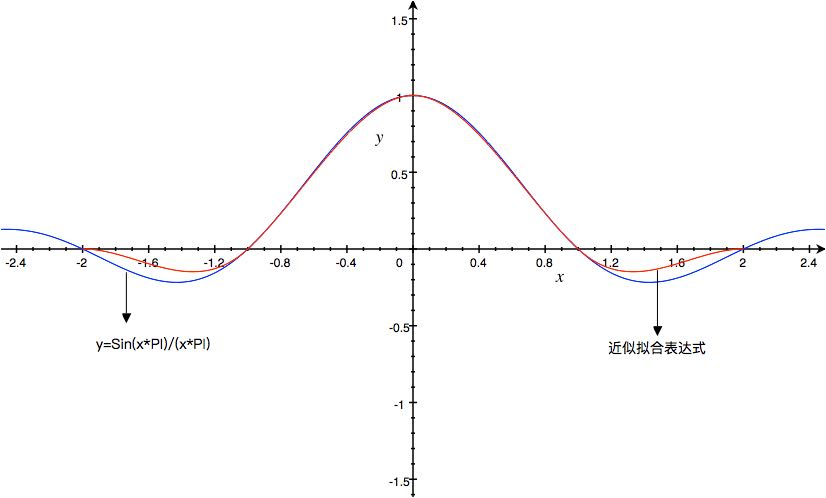
当a取值为-1
公式如下:
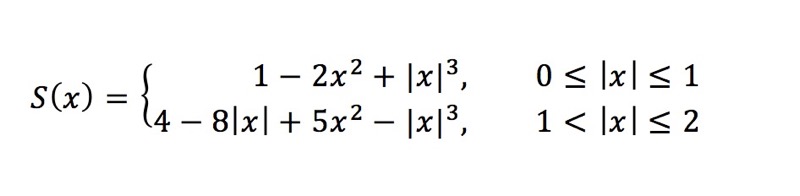
此时,逼近的函数是y = sin(x*PI)/(x*PI),如图
当a取值为-0.5
公式如下:
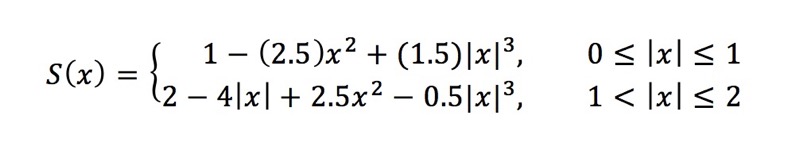
此时对应三次Hermite样条
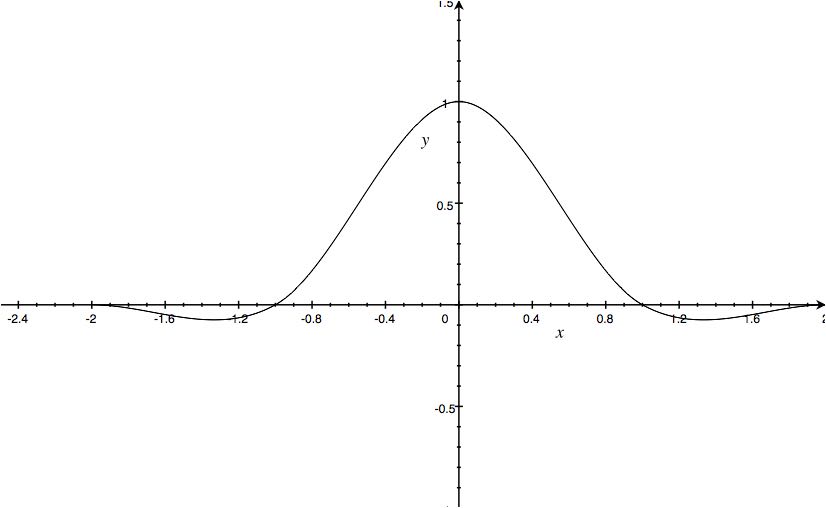
不同a的简单对比
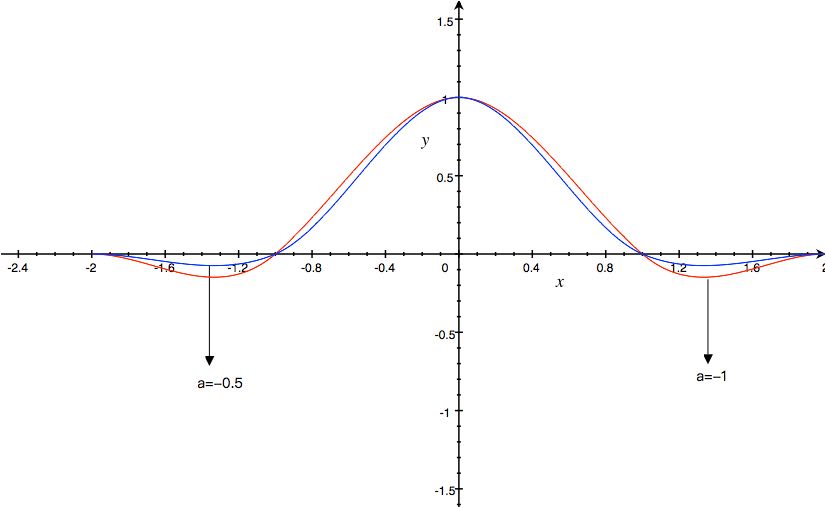
推导
可参考:
关于网上的一些推导公式奇怪实现
在网上查找了不少相关资料,发现有不少文章中都用到了以下这个奇怪的公式(譬如百度搜索双立方插值)
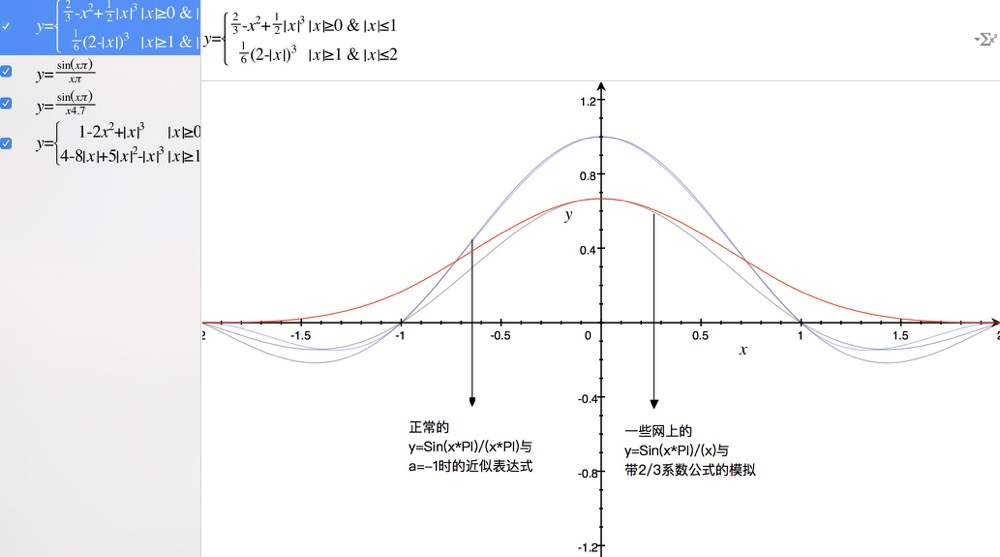
一般这些文章中都声称这个公式是用来近似y = sin(x*PI)/(x)
但事实上,进过验证,它与y = sin(x*PI)/(x)相差甚远(如上图中是将sin函数缩放到合理系数后比对)
由于类似的文章较多,年代都比较久远,无从得知最初的来源
可能是某文中漏掉了分母的PI,亦或是这个公式只是某文自己实现的一个采样公式,与sin无关,然后被误传了。
这里都无从考据,仅此记录,避免疑惑。
另一种基于系数的实现
可以参考:图像处理(一)bicubic解释推导
像这类的实现就是直接计算最原始的系数,然后通过16个像素点计算不同系数值,最终计算出目标像素
本质是一样的,只不过是没有基于最终的卷积方程计算而已(也就是说在原始理论阶段没有推成插值公式,而是直接解出系数并计算)。
代码实现在github项目中可看到,参考最后的开源项目
代码实现
以下是JavaScript代码实现的插值核心方程
/**
* 采样公式的常数A取值,调整锐化与模糊
* -0.5 三次Hermite样条
* -0.75 常用值之一
* -1 逼近y = sin(x*PI)/(x*PI)
* -2 常用值之一
*/
const A = -0.5;
function interpolationCalculate(x) {
const absX = x > 0 ? x : -x;
const x2 = x * x;
const x3 = absX * x2;
if (absX <= 1) {
return 1 - (A + 3) * x2 + (A + 2) * x3;
} else if (absX <= 2) {
return -4 * A + 8 * A * absX - 5 * A * x2 + A * x3;
}
return 0;
}
以上是卷积方程的核心实现。下面则是一套完整的实现
/**
* 采样公式的常数A取值,调整锐化与模糊
* -0.5 三次Hermite样条
* -0.75 常用值之一
* -1 逼近y = sin(x*PI)/(x*PI)
* -2 常用值之一
*/
const A = -1;
function interpolationCalculate(x) {
const absX = x >= 0 ? x : -x;
const x2 = x * x;
const x3 = absX * x2;
if (absX <= 1) {
return 1 - (A + 3) * x2 + (A + 2) * x3;
} else if (absX <= 2) {
return -4 * A + 8 * A * absX - 5 * A * x2 + A * x3;
}
return 0;
}
function getPixelValue(pixelValue) {
let newPixelValue = pixelValue;
newPixelValue = Math.min(255, newPixelValue);
newPixelValue = Math.max(0, newPixelValue);
return newPixelValue;
}
/**
* 获取某行某列的像素对于的rgba值
* @param {Object} data 图像数据
* @param {Number} srcWidth 宽度
* @param {Number} srcHeight 高度
* @param {Number} row 目标像素的行
* @param {Number} col 目标像素的列
*/
function getRGBAValue(data, srcWidth, srcHeight, row, col) {
let newRow = row;
let newCol = col;
if (newRow >= srcHeight) {
newRow = srcHeight - 1;
} else if (newRow < 0) {
newRow = 0;
}
if (newCol >= srcWidth) {
newCol = srcWidth - 1;
} else if (newCol < 0) {
newCol = 0;
}
let newIndex = (newRow * srcWidth) + newCol;
newIndex *= 4;
return [
data[newIndex + 0],
data[newIndex + 1],
data[newIndex + 2],
data[newIndex + 3],
];
}
function scale(data, width, height, newData, newWidth, newHeight) {
const dstData = newData;
// 计算压缩后的缩放比
const scaleW = newWidth / width;
const scaleH = newHeight / height;
const filter = (dstCol, dstRow) => {
// 源图像中的坐标(可能是一个浮点)
const srcCol = Math.min(width - 1, dstCol / scaleW);
const srcRow = Math.min(height - 1, dstRow / scaleH);
const intCol = Math.floor(srcCol);
const intRow = Math.floor(srcRow);
// 计算u和v
const u = srcCol - intCol;
const v = srcRow - intRow;
// 真实的index,因为数组是一维的
let dstI = (dstRow * newWidth) + dstCol;
dstI *= 4;
// 存储灰度值的权重卷积和
const rgbaData = [0, 0, 0, 0];
// 根据数学推导,16个点的f1*f2加起来是趋近于1的(可能会有浮点误差)
// 因此就不再单独先加权值,再除了
// 16个邻近点
for (let m = -1; m <= 2; m += 1) {
for (let n = -1; n <= 2; n += 1) {
const rgba = getRGBAValue(
data,
width,
height,
intRow + m,
intCol + n,
);
// 一定要正确区分 m,n和u,v对应的关系,否则会造成图像严重偏差(譬如出现噪点等)
// F(row + m, col + n)S(m - v)S(n - u)
const f1 = interpolationCalculate(m - v);
const f2 = interpolationCalculate(n - u);
const weight = f1 * f2;
rgbaData[0] += rgba[0] * weight;
rgbaData[1] += rgba[1] * weight;
rgbaData[2] += rgba[2] * weight;
rgbaData[3] += rgba[3] * weight;
}
}
dstData[dstI + 0] = getPixelValue(rgbaData[0]);
dstData[dstI + 1] = getPixelValue(rgbaData[1]);
dstData[dstI + 2] = getPixelValue(rgbaData[2]);
dstData[dstI + 3] = getPixelValue(rgbaData[3]);
};
// 区块
for (let col = 0; col < newWidth; col += 1) {
for (let row = 0; row < newHeight; row += 1) {
filter(col, row);
}
}
}
export default function bicubicInterpolation(imgData, newImgData) {
scale(imgData.data,
imgData.width,
imgData.height,
newImgData.data,
newImgData.width,
newImgData.height);
return newImgData;
}
运行效果
分别用三种算法对一个图进行放大,可以明显的看出双立方插值效果最好
最临近插值

双线性插值

双立方(三次卷积)插值

开源项目
这个项目里用JS实现了几种插值算法,包括(最邻近值,双线性,三次卷积-包括两种不同实现等)
https://github.com/dailc/image-process


 浙公网安备 33010602011771号
浙公网安备 33010602011771号