机器学习基石笔记（二）

二、Why can machines Learn？

　　  之前我们在讨论Ein和Eout的问题的时候，假设了假设空间H是有限的，为M个，但是对于M的大小有一些问题，为了保证Ein等于Eout我们想要比较小的M，但为了保证Ein=0，我们需要有很多的选择需要去选，这样就要求M比较大。这个问题继续发散下去就是：如果M是无限大的呢？这当然是一个我们必须得考虑的问题。

　　　如下图所示，绿色的是我们之前得到的，但在M无穷大的时候，实际上是有一个mh可以来代替的，如何得到这个mh，是我们下面的重要工作....

　　如何理解一个假设空间在M无穷大的时候，我们可以找到一个mh来代替这件事呢？ 想象在二维平面上有一点，我们用直线去给这个点做二分类，虽然可以画出无数的直线，但事实上只有两类的直线，把点分为正的和分为负的。这里林老师用了一个effective(N),它有两个性质：1、可以用来代替M 2、远小于2的N次方。这是一个很好的信号，至少我们看到了成功的曙光..

　　后面花了很长的篇幅推导了一些假设空间的mH,给我们的收获就是：mH是polynomial的，这又是一个很好的讯息，将我们的mH降到了多项式级别的难度了。

　　然后是一个概念性的问题，break point：if no k inputs can be shattered by H, call k a break point for H，总结规律发现，mH跟break point有着对应的关系..但暂时还只是一个猜想。这里还有一个问题就是什么叫shatter：能被shatter的意思是，存在一种数据的分布情况（点的位置），它的所有种类情况（每个点的类别）都能被成功分类。

　　之后引出了Bounding Function的概念。所谓bounding function，就是 maximum possible mH(N) when break point = k ，经过一番推断，我们可以得到下面的表格：

　　

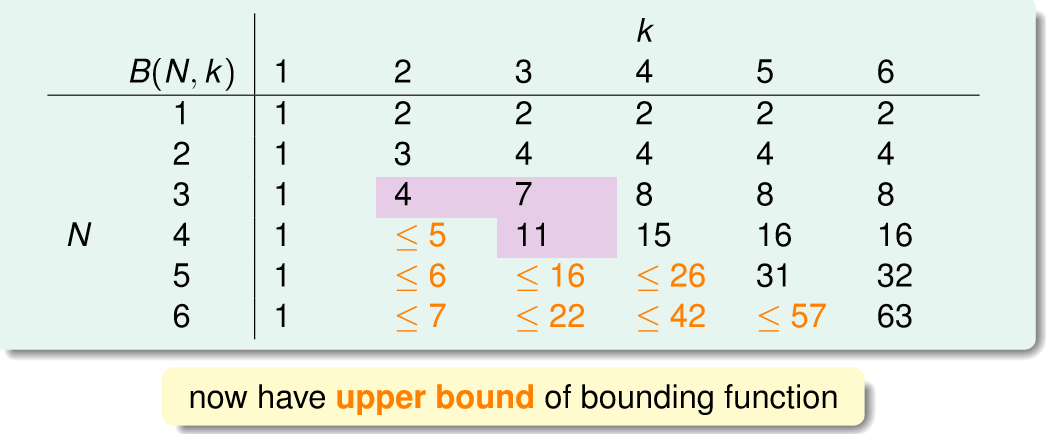
也就可以得到：

　　

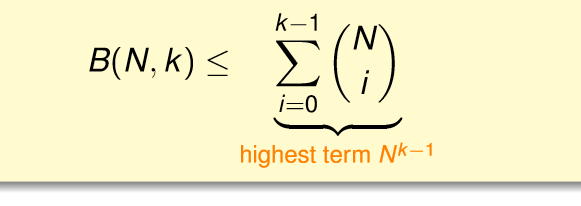
　　这个式子是可以去掉不等号的...但是证明起来很麻烦.

这个给我们什么启示呢？我们可以只用break point就得到mH(N)的上界。

后面有一个使用mH（N）代替M的时候需要做的变化的证明...我表示看着还行，推肯定推不出来了，也不想在上面深究..

总之，经过上面的一长串的研究，我们可以得到这样一个结论：

　　

下面这幅图也很好的说明我们的算法学习成功到底经历了多大的困难............

　　

 

 　　接下来就是大名鼎鼎的VC维了，首先还是要引出定义：VC维就是使得mH（N）等于2的N次方的最大的N的值，结合之前的理解就是，最小的break point减去1的值

　 　VC维可以给我们一个不错的保证：只有你的vc bound是有限的，那么你就可以做到Eout（g）约等于Ein（g），无论是什么样的算法、分布以及目标函数。

　　下面的是个易错题....已经做错好多次了，主要还是概念上的问题，所有和存在这两种情况要分清楚。

　　也就是上面说的我们在shatter的时候，对于每个N，只要存在一种情况可以shatter，就是可shatter的。

　　

　　接下来是dvc的证明，前面的好理解，我想解释一下dvc<=d+1的情况

　　

　　上图？肯定不能使蓝色的圈圈，因为那样就可分了，所以必然是红色的叉叉才能符合不可分的条件。

　　

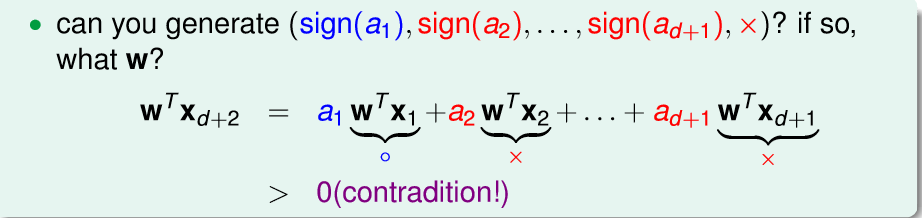
　　然而我们一旦构造出上图的条件就会得到矛盾，然后证明就结束了。关键是要理解为什么可以这样故意构造条件呢？因为shatter是相对于x来说的，也就是对于所以的x，在他们任意lebel y的组合下都可以分隔开，才算shatter，所以自然可以构造出条件。

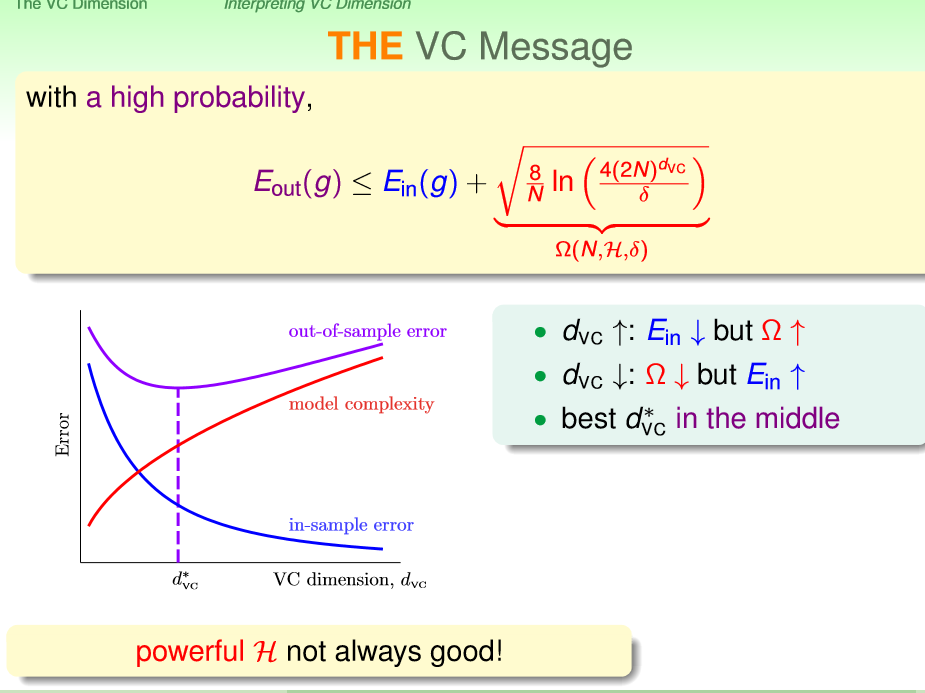
再然后我们可以看到下面这个熟悉的图，vc维可以理解为一个模型的复杂度

然后又是machine learning里面常用的trick了，虽然理论保证需要我们的N是dvc的10000倍，但实际使用的时候10倍的dvc就可以有不错的效果了，也很好理解，因为我们在推导到VC维的时候，用来太多太多的loose的upper bound了。

接下来谈到err function对算法的影响，进而引出了一个问题：如果有一个场景，我们可以容忍把-1判断成1，但完全不能允许把1判断成-1，怎么办？解决方法就是在err function上做工作，我们可以再算法把-1判断成1的时候，加大惩罚力度，如下：

这样最后学习到的结果就是有偏置的了，我们能够做到尽量避免自己不喜欢的结果出现。上面这个方法的另外一个角度就是，err函数不变，但是把相应的样本的数量提高1000倍，这个效果是一致的。这种数据增益的方法也很常用。