栈:
文中举例解释均为尚硅谷数据结构与算法教程中的。【传送门】
目录:
1、栈是什么
2、实现栈
2-1、使用数组模拟栈
2-2、使用单链表模拟栈
2-3、实现栈全部源码
3、使用栈实现简易计算器
3-1、步骤
3-2、源码
4、使用后缀表达式完成计算器实现
4-1、前缀表达式
4-2、中缀表达式
4-3、后缀表达式
4-4、实现
4-4-1、步骤
4-4-2、使用后缀表达式计算结果
4-4-3、将中缀表达式转后缀表达式
4-4-4、源码
1、栈是什么
栈是一种数据结构,它的特点就是先进后出。

它的特点就像手枪弹夹一样,你先压进去的子弹是后打出来的,而最后打出来的子弹却是最先打出来的。
你也可以理解它是一个水桶,在倒水的时候,你原先最早弄进去的水是最后被倒出来的,而你最后弄进去的水却是最早被倒出来的。
然后来画一个图。
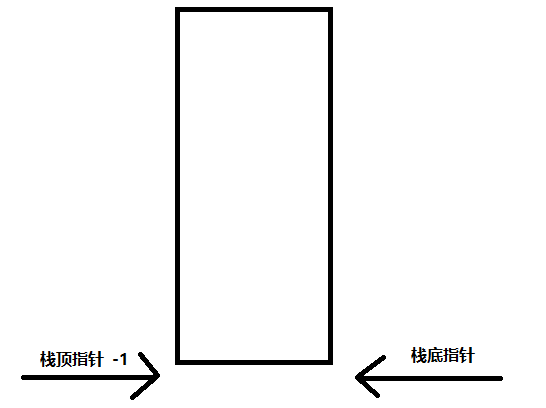
那么可以看出来,栈中有两个指针,一个指向栈顶,一个指向栈底。
那么当我们添加两个元素以后就是这样:
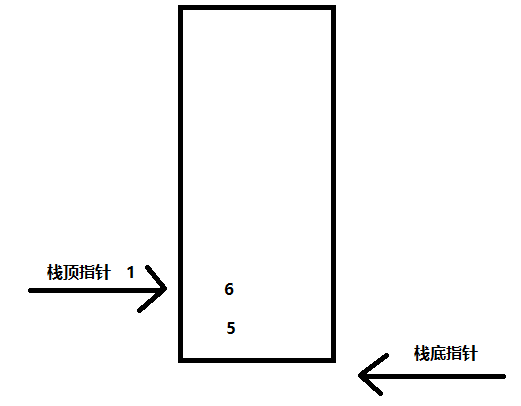
我们可以发现栈顶指针变了,但是栈底指针没变,那么可以得出结论,栈顶指针指向了栈的顶部,而栈底指针指向了栈的底部。
栈顶指针会随着栈顶变化,而栈底指针不会改变。
2、实现栈
2-1、使用数组模拟栈

1 /*使用数组模拟栈*/ 2 class ArrayStack { 3 /*这个top代表着栈顶*/ 4 private int top = -1; 5 /*栈的总容量*/ 6 private int maxSize; 7 /*实际存储数据的数组*/ 8 private int[] array; 9 10 public ArrayStack(int maxSize) { 11 this.maxSize = maxSize; 12 array = new int[maxSize]; 13 } 14 15 /*是否已满*/ 16 public boolean isFull() { 17 return top == maxSize - 1; 18 } 19 20 /*是否为空*/ 21 public boolean isEmpty() { 22 return top == -1; 23 } 24 25 /*入栈*/ 26 public boolean push(int value) { 27 /*首先判断是否为空*/ 28 if (isFull()) { 29 throw new RuntimeException("栈已满!"); 30 } 31 array[++top] = value; 32 return true; 33 } 34 35 /*出栈*/ 36 public int pop() { 37 if (isEmpty()) { 38 throw new RuntimeException("栈为空!"); 39 } 40 return array[top--]; 41 } 42 43 /*遍历所有*/ 44 public void display() { 45 if (isEmpty()) { 46 System.out.println("栈为空"); 47 return; 48 } 49 for (int i = top; i >= 0; i--) { 50 System.out.println(array[i]); 51 } 52 } 53 }
属性
top:栈顶指针
maxSize:数组的大小
array:实际存储数据的数组
方法:
isFull:栈是否已满
isEmpty:栈是否为空
push:入栈
pop:出栈/弹栈
display:遍历查看栈中所有数据(并没有取出来,只是看看)
注意:这里没有考虑扩容的问题
2-2、使用单链表模拟栈

1 /*使用单链表模拟栈*/ 2 class SingleLinkedStack { 3 /*单链表的头节点*/ 4 private StackNode head = new StackNode(-1); 5 /*栈顶数量*/ 6 private int top = -1; 7 /*栈存储的最大数量*/ 8 private int maxSize; 9 10 public SingleLinkedStack(int maxSize) { 11 this.maxSize = maxSize; 12 } 13 14 /*是否已满*/ 15 public boolean isFull() { 16 return top == maxSize - 1; 17 } 18 19 /*是否为空,头节点下没有数据或者说栈顶索引为-1,都代表着栈为空*/ 20 public boolean isEmpty() { 21 return head.next == null || top == -1; 22 } 23 24 /*入栈*/ 25 public boolean push(StackNode stackNode) { 26 if (isFull()) { 27 throw new RuntimeException("栈已满!"); 28 } 29 /*那么加入到最后端*/ 30 StackNode temp = head; 31 while (true) { 32 if (temp.next == null) { 33 temp.next = stackNode; 34 /*当前位置也要++*/ 35 top++; 36 return true; 37 } 38 temp = temp.next; 39 } 40 } 41 42 /*出栈*/ 43 public StackNode pop() { 44 /*先判断是否为空*/ 45 if (isEmpty()) { 46 throw new RuntimeException("栈为空!"); 47 } 48 /*直接取出最后一位*/ 49 StackNode temp = head; 50 while (true) { 51 if (temp.next.next == null) { 52 /*那么这个时候temp.next就是最后一位了*/ 53 /*temp.next就是需要移除的那一个*/ 54 StackNode result = temp.next; 55 temp.next = null; 56 top--; 57 return result; 58 } 59 temp = temp.next; 60 } 61 } 62 63 64 } 65 66 /*链表节点*/ 67 class StackNode { 68 public int no; 69 public StackNode next; 70 71 public StackNode(int no) { 72 this.no = no; 73 } 74 75 @Override 76 public String toString() { 77 return "StackNode{" + 78 "no=" + no + 79 '}'; 80 } 81 }
SingleLinkedStack:单链表
属性:
head:头结点
top:栈顶指针
maxSize:存储最大数量
方法:
isFull:栈是否已满
isEmpty:栈是否为空
push:入栈
pop:出栈
StackNode:单链表中的每一个节点
2-3、实现栈全部源码

1 package t5; 2 3 /** 4 * @author 自在仙 5 * @create 2020年04月22 17:39 6 */ 7 public class StackDemo { 8 9 public static void main(String[] args) { 10 /* ArrayStack arrayStack = new ArrayStack(10); 11 arrayStack.push(10); 12 arrayStack.push(50); 13 arrayStack.push(30); 14 arrayStack.pop(); 15 arrayStack.display();*/ 16 StackNode stackNode1 = new StackNode(1); 17 StackNode stackNode2 = new StackNode(2); 18 StackNode stackNode3 = new StackNode(3); 19 StackNode stackNode4 = new StackNode(4); 20 StackNode stackNode5 = new StackNode(5); 21 StackNode stackNode6 = new StackNode(6); 22 StackNode stackNode7 = new StackNode(7); 23 StackNode stackNode8 = new StackNode(8); 24 StackNode stackNode9 = new StackNode(9); 25 StackNode stackNode10 = new StackNode(10); 26 StackNode stackNode11 = new StackNode(11); 27 28 SingleLinkedStack singleLinkedStack = new SingleLinkedStack(10); 29 singleLinkedStack.push(stackNode1); 30 singleLinkedStack.push(stackNode2); 31 singleLinkedStack.push(stackNode3); 32 singleLinkedStack.push(stackNode4); 33 singleLinkedStack.push(stackNode5); 34 singleLinkedStack.push(stackNode6); 35 singleLinkedStack.push(stackNode7); 36 singleLinkedStack.push(stackNode8); 37 singleLinkedStack.push(stackNode9); 38 singleLinkedStack.push(stackNode10); 39 40 System.out.println(singleLinkedStack.pop()); 41 System.out.println(singleLinkedStack.pop()); 42 System.out.println(singleLinkedStack.pop()); 43 System.out.println(singleLinkedStack.pop()); 44 System.out.println(singleLinkedStack.pop()); 45 System.out.println(singleLinkedStack.pop()); 46 System.out.println(singleLinkedStack.pop()); 47 System.out.println(singleLinkedStack.pop()); 48 System.out.println(singleLinkedStack.pop()); 49 System.out.println(singleLinkedStack.pop()); 50 } 51 } 52 53 /*使用数组模拟栈*/ 54 class ArrayStack { 55 /*这个top代表着栈顶*/ 56 private int top = -1; 57 /*栈的总容量*/ 58 private int maxSize; 59 /*实际存储数据的数组*/ 60 private int[] array; 61 62 public ArrayStack(int maxSize) { 63 this.maxSize = maxSize; 64 array = new int[maxSize]; 65 } 66 67 /*是否已满*/ 68 public boolean isFull() { 69 return top == maxSize - 1; 70 } 71 72 /*是否为空*/ 73 public boolean isEmpty() { 74 return top == -1; 75 } 76 77 /*入栈*/ 78 public boolean push(int value) { 79 /*首先判断是否为空*/ 80 if (isFull()) { 81 throw new RuntimeException("栈已满!"); 82 } 83 array[++top] = value; 84 return true; 85 } 86 87 /*出栈*/ 88 public int pop() { 89 if (isEmpty()) { 90 throw new RuntimeException("栈为空!"); 91 } 92 return array[top--]; 93 } 94 95 /*遍历所有*/ 96 public void display() { 97 if (isEmpty()) { 98 System.out.println("栈为空"); 99 return; 100 } 101 for (int i = top; i >= 0; i--) { 102 System.out.println(array[i]); 103 } 104 } 105 } 106 107 /*使用单链表模拟栈*/ 108 class SingleLinkedStack { 109 /*单链表的头节点*/ 110 private StackNode head = new StackNode(-1); 111 /*栈顶数量*/ 112 private int top = -1; 113 /*栈存储的最大数量*/ 114 private int maxSize; 115 116 public SingleLinkedStack(int maxSize) { 117 this.maxSize = maxSize; 118 } 119 120 /*是否已满*/ 121 public boolean isFull() { 122 return top == maxSize - 1; 123 } 124 125 /*是否为空,头节点下没有数据或者说栈顶索引为-1,都代表着栈为空*/ 126 public boolean isEmpty() { 127 return head.next == null || top == -1; 128 } 129 130 /*入栈*/ 131 public boolean push(StackNode stackNode) { 132 if (isFull()) { 133 throw new RuntimeException("栈已满!"); 134 } 135 /*那么加入到最后端*/ 136 StackNode temp = head; 137 while (true) { 138 if (temp.next == null) { 139 temp.next = stackNode; 140 /*当前位置也要++*/ 141 top++; 142 return true; 143 } 144 temp = temp.next; 145 } 146 } 147 148 /*出栈*/ 149 public StackNode pop() { 150 /*先判断是否为空*/ 151 if (isEmpty()) { 152 throw new RuntimeException("栈为空!"); 153 } 154 /*直接取出最后一位*/ 155 StackNode temp = head; 156 while (true) { 157 if (temp.next.next == null) { 158 /*那么这个时候temp.next就是最后一位了*/ 159 /*temp.next就是需要移除的那一个*/ 160 StackNode result = temp.next; 161 temp.next = null; 162 top--; 163 return result; 164 } 165 temp = temp.next; 166 } 167 } 168 169 170 } 171 172 /*链表节点*/ 173 class StackNode { 174 public int no; 175 public StackNode next; 176 177 public StackNode(int no) { 178 this.no = no; 179 } 180 181 @Override 182 public String toString() { 183 return "StackNode{" + 184 "no=" + no + 185 '}'; 186 } 187 }
3、使用栈实现简易计算器
3-1、步骤
给定的是一个比如这样的:700*2*2-5+1-5+3-4表达式,这是一个算式撒,要计算出这个表达式的结果
步骤:
1、首先创建一个index用来遍历表达式,然后创建一个数栈用来存放数值,然后创建一个符号栈用来存放操作符
2、然后开始遍历字符串
3、发现当前是一个数字,那么判断其后面是否为数字,如果是数字需要叠加,然后入数栈
4、如果当前是一个符号,分下情况
4-1、如果当前符号栈为空,那么就直接入符号栈
4-2、如果当前符号栈中有数据,那么就进行比较,如果当前符号的优先级大于栈顶操作符的优先级,那么直接入符号栈,如果当前符号的优先级小于或者等于栈顶符号的优先级,那么就需要从数栈中弹出两个数,然后再从符号栈中弹出
一个符号,进行计算,计算结果再入数栈,,然后再将当前操作符入符号栈
5、当表达式遍历完成以后,符号栈中肯定还有剩余的符号
6、从符号栈中弹出一个符号,然后从数栈中弹出两个数,进行计算,计算完后再压入数栈,重复此操作,直到符号栈为空
7、此时数栈还剩余一个数值,这个数字键就是结果。
3-2、源码

1 package t5; 2 3 import java.util.Stack; 4 5 /** 6 * @author 自在仙 7 * @create 2020年04月26 15:52 8 * 计算器 9 */ 10 public class Calculator { 11 12 public static void main(String[] args) { 13 String input = "700*2*2-5+1-5+3-4"; 14 15 System.out.println(calculator1(input)); 16 } 17 18 /*计算方法1*//*这个我们直接操作的就是中缀表达式*/ 19 public static int calculator1(String expression) { 20 /** 21 * 1. 通过一个 index 值(索引),来遍历我们的表达式 22 * 2. 如果我们发现是一个数字, 就直接入数栈 23 * 3. 如果发现扫描到是一个符号, 就分如下情况 24 * 3.1 如果发现当前的符号栈为 空,就直接入栈 25 * 3.2 如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符, 26 * 就需要从数栈中pop出两个数,在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈, 27 * 如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈. 28 * 4. 当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行. 29 * 5. 最后在数栈只有一个数字,就是表达式的结果 30 */ 31 /*记录当前遍历的下标*/ 32 int index = 0; 33 /*数栈*/ 34 CalculatorStack numStack = new CalculatorStack(10); 35 /*符号栈*/ 36 CalculatorStack oprStack = new CalculatorStack(10); 37 /*遍历*/ 38 while (true) { 39 /*当前遍历表达式的某一个数据*/ 40 int currentChar = expression.charAt(index); 41 /*判断是否为数字,如果是就直接入栈*/ 42 /*如果是数字,直接入数栈,否则符号就另行操作*/ 43 if (CalculatorStack.isOperator(currentChar)) { 44 /*符号的情况*/ 45 /*先判断符号栈是否为空*/ 46 if (oprStack.isEmpty()) { 47 /*直接入栈*/ 48 oprStack.push(currentChar); 49 } else { 50 /*否则说明符号栈有东西,那么就需要偷看符号栈栈顶的那一个,然后和当前的符号进行比较*/ 51 int oprTop = oprStack.peek(); 52 /*比较,如果当前操作符小于或者等于栈顶操作符,那么就需要操作,否则就直接入符号栈*/ 53 int i = CalculatorStack.operatorLevel(currentChar, oprTop); 54 if (i == 1) { 55 oprStack.push(currentChar); 56 } else { 57 /*拿数栈的两个数字,然后再从符号栈中pop出一个数进行运算,然后存入数栈*/ 58 int num1 = numStack.pop(); 59 int num2 = numStack.pop(); 60 int opr = oprStack.pop(); 61 int result = CalculatorStack.calculatorEquation(num1, num2, opr); 62 /*把结果加到数栈中*/ 63 numStack.push(result); 64 /*把当前操作符加入到符号栈*/ 65 oprStack.push(currentChar); 66 } 67 } 68 } else { 69 /*数字的情况,需要判断是否为多位*/ 70 /*记录每一次当前数字,然后用于判断后面是否还有*/ 71 String numTemp = currentChar - 48 + ""; 72 /*判断是不是最后一位,如果是就不要往后面判断了*/ 73 /*if (index!=expression.length()-1){ 74 *//*判断后面是不是数字*//* 75 if (!CalculatorStack.isOperator(expression.charAt(index + 1))) { 76 *//*如果是数字,那么叠加一下*//* 77 numTemp += expression.charAt(++index); 78 } 79 }*/ 80 /*判断是否为最后一位*/ 81 if (index != expression.length() - 1) { 82 /*否则就看后面的*/ 83 while (true) { 84 /*如果后一位不是操作符,那么拼接*/ 85 if (!CalculatorStack.isOperator(expression.charAt(index + 1))) { 86 numTemp += expression.charAt(index + 1) + ""; 87 ++index; 88 } else { 89 break; 90 } 91 } 92 } 93 numStack.push(Integer.valueOf(numTemp)); 94 } 95 /*判断是否完成*/ 96 if (index == expression.length() - 1) { 97 break; 98 } else { 99 index++; 100 } 101 } 102 103 /*运算完成,将数栈和符号栈中的数据进行运算*/ 104 while (!oprStack.isEmpty()) { 105 int num1 = numStack.pop(); 106 int num2 = numStack.pop(); 107 int opr = oprStack.pop(); 108 int result = CalculatorStack.calculatorEquation(num1, num2, opr); 109 numStack.push(result); 110 } 111 return numStack.pop(); 112 } 113 114 115 } 116 117 class CalculatorStack { 118 /*最大长度*/ 119 private int maxSize; 120 /*栈顶*/ 121 private int top = -1; 122 /*存储数据的数组*/ 123 private int[] data; 124 125 public CalculatorStack(int maxSize) { 126 this.maxSize = maxSize; 127 data = new int[maxSize]; 128 } 129 130 /*是否已满*/ 131 public boolean isFull() { 132 return top == maxSize - 1; 133 } 134 135 /*是否为空*/ 136 public boolean isEmpty() { 137 return top == -1; 138 } 139 140 /*出栈*/ 141 public int pop() { 142 if (isEmpty()) { 143 throw new RuntimeException("栈已满!"); 144 } 145 return data[top--]; 146 } 147 148 /*入栈*/ 149 public void push(int value) { 150 if (isFull()) { 151 throw new RuntimeException("栈已满!"); 152 } 153 data[++top] = value; 154 } 155 156 /*偷看栈顶*/ 157 public int peek() { 158 if (isEmpty()) { 159 throw new RuntimeException("栈为空"); 160 } 161 return data[top]; 162 } 163 164 /*判断是否为运算符*/ 165 public static boolean isOperator(int value) { 166 return value == '+' || value == '-' || value == '*' || value == '/'; 167 } 168 169 170 /** 171 * 比较运算符等级 172 * 173 * @param operator1 操作符1 174 * @param operator2 操作符2 175 * @return 如果相等 0 176 * 如果operator1 > operator2 1 177 * 如果operator2 > operator1 -1 178 */ 179 public static int operatorLevel(int operator1, int operator2) { 180 if (((operator1 == '+' || operator1 == '-') && (operator2 == '+' || operator2 == '-')) || (operator1 == '*' || operator1 == '/') && (operator2 == '*' || operator2 == '/')) { 181 return 0; 182 } 183 /*2比1大的情况*/ 184 if (((operator1 == '+' || operator1 == '-') && (operator2 == '*' || operator2 == '/'))) { 185 return -1; 186 } 187 /*1比2大的情况*/ 188 if (((operator1 == '*' || operator1 == '/') && (operator2 == '+' || operator2 == '-'))) { 189 return 1; 190 } 191 throw new RuntimeException("操作符无效!"); 192 } 193 194 /** 195 * 计算算式 196 * 197 * @param value1 数值1 198 * @param value2 数值2 199 * @param expression 操作符 200 * @return 结果 201 */ 202 public static int calculatorEquation(int value1, int value2, int expression) { 203 switch (expression) { 204 case '+': 205 return value1 + value2; 206 case '-': 207 /*注意,如果是减法或者除法,都是用后面的一个减去前面的一个*/ 208 return value2 - value1; 209 case '*': 210 return value1 * value2; 211 case '/': 212 return value2 / value1; 213 } 214 throw new RuntimeException("操作符无效!"); 215 } 216 217 }
4、使用后缀表达式完成计算器实现
4-1、前缀表达式
前缀表达式也叫波兰表达式。
前缀表达式中,符号位于数字的前面,例如:(3+4)x5-6对应的前缀表达式为 - * + 3 4 5 6
前缀表达式的计算:

1 从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果 2 3 例如: (3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下: 4 5 1、从右至左扫描,将6、5、4、3压入堆栈 6 2、遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素),计算出3+4的值,得7,再将7入栈 7 3、接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈 8 4、最后是-运算符,计算出35-6的值,即29,由此得出最终结果
4-2、中缀表达式
中缀表达式就是我们平时写的算式,例如:(3+4)x5-6,这种表达式的计算方法就是我们前面实现的简易计算器.。
4-3、后缀表达式
也叫逆波兰表达式,后缀表达式与前缀表达式类似,不同之处就是后缀表达式的符号位于数字后面,前缀是符号位于数字的前面。
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
再例如:

后缀表达式的计算方法:

1 从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果 2 3 例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下: 4 5 1、从左至右扫描,将3和4压入堆栈; 6 2、遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈; 7 3、将5入栈; 8 4、接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈; 9 5、将6入栈; 10 6、最后是-运算符,计算出35-6的值,即29,由此得出最终结果
4-4、实现
4-4-1、步骤
首先我们要明白,后缀表达式计算显然比我们直接使用中缀表达式更加的简单,但是我们输入的表达式却是中缀表达式,所以这就涉及到一个将中缀表达式转换为后缀表达式。那么我们实现的时候就要注意将中缀表达式转换为后缀表达式。
步骤:

1 1、将中缀表达式转换为后缀表达式 2 2、计算后缀表达式的值 3 4 5 6 1------:将中缀表达式转换为后缀表达式的步骤: 7 1) 初始化两个栈:运算符栈s1和储存中间结果的栈s2; 8 2) 从左至右扫描中缀表达式; 9 3) 遇到操作数时,将其压s2; 10 4) 遇到运算符时,比较其与s1栈顶运算符的优先级: 11 1.如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈; 12 2.否则,若优先级比栈顶运算符的高,也将运算符压入s1; 13 3.否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4.1)与s1中新的栈顶运算符相比较; 14 5) 遇到括号时: 15 (1) 如果是左括号“(”,则直接压入s1 16 (2) 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃 17 6) 重复步骤2至5,直到表达式的最右边 18 7) 将s1中剩余的运算符依次弹出并压入s2 19 8) 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式 20 21 22 23 2------:计算后缀表达式的值: 24 从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
4-4-2、使用后缀表达式计算结果

1 /** 2 * 逆波兰计算器 3 * 传入后缀表达式字符串,返回计算结果 4 * 5 * @param suffixExpression 后缀表达式字符串 6 * @return 7 */ 8 public static int calculateForString(String suffixExpression) { 9 return calculateForStringArray(suffixExpression.split(" ")); 10 } 11 12 /** 13 * 逆波兰计算器 14 * 传入后缀表达式拆分后的数组,返回计算结果 15 * 16 * @param suffixExpressionArray 后缀表达式拆分后的数组 17 * @return 18 */ 19 public static int calculateForStringArray(String[] suffixExpressionArray) { 20 ArrayList<String> strings = new ArrayList<>(); 21 for (int i = 0; i < suffixExpressionArray.length; i++) { 22 strings.add(suffixExpressionArray[i]); 23 } 24 return calculateForList(strings); 25 } 26 27 /** 28 * 逆波兰计算器 29 * 传入后缀表达式字符串,返回计算结果 30 * 31 * @param suffixExpressionList 后缀表达式拆分后的集合 32 * @return 33 */ 34 public static int calculateForList(List<String> suffixExpressionList) { 35 /* 36 * 从左至右扫描表达式, 37 * 遇到数字时,将数字压入堆栈, 38 * 遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈; 39 * 重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果 40 * */ 41 /*先创建一个栈,用来存放数字*/ 42 Stack<Integer> numStack = new Stack<>(); 43 for (String item : suffixExpressionList) { 44 /*判断是不是数字,如果是数字,直接入栈*/ 45 if (item.matches("\\d+")) { 46 numStack.push(Integer.valueOf(item)); 47 } else { 48 /*两个数*/ 49 Integer num1 = numStack.pop(); 50 Integer num2 = numStack.pop(); 51 /*如果是符号,那么从栈中拿两个数然后计算后并放回栈中*/ 52 switch (item) { 53 case "+": 54 numStack.push(num1 + num2); 55 break; 56 case "-": 57 numStack.push(num2 - num1); 58 break; 59 case "*": 60 numStack.push(num1 * num2); 61 break; 62 case "/": 63 numStack.push(num2 / num1); 64 break; 65 default: 66 throw new RuntimeException("操作符错误!"); 67 } 68 } 69 } 70 return numStack.pop(); 71 }
需要注意的是这里有三个方法,实际上调用的话,你可以直接传入后缀表达式字符串,或者拆分为数组的后缀表达式,或者拆分为集合的后缀表达式。
4-4-3、将中缀表达式转后缀表达式

1 /*将一个中缀表达式转换为后缀表达式*/ 2 public static List<String> infixExpressionToToSuffixExpression(List<String> infixExpression) { 3 /*1、初始化两个栈,运算符s1和存储中间结果的s2*/ 4 /*运算符s1*/ 5 Stack<String> s1 = new Stack<>(); 6 /*中间结果s2*/ 7 Stack<String> s2 = new Stack<>(); 8 9 for (int i = 0; i < infixExpression.size(); i++) { 10 /*2、从左到右遍历*/ 11 String item = infixExpression.get(i); 12 /*3、遇到操作数的时候,将其压入s2*/ 13 /*判断是否为数字*/ 14 if (item.matches("\\d+")) { 15 s2.push(item); 16 } else if (isOperator(item)) {/*4、判断是否为运算符*/ 17 /*4-1、如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;*/ 18 while (true) { 19 /*s1为空或者栈顶为左括号*/ 20 if (s1.isEmpty() || s1.peek().equals("(")) { 21 s1.push(item); 22 break; 23 } else { 24 /* 4-2.否则,若优先级比栈顶运算符的高,也将运算符压入s1; 25 4-3.否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4.1)与s1中新的栈顶运算符相比较;*/ 26 /*拿到栈顶和当前运算符的优先级*/ 27 String s1Top = s1.peek(); 28 int t1TopValue = getOperatorPriorityValue(s1Top); 29 int itemValue = getOperatorPriorityValue(item); 30 if (itemValue > t1TopValue) {/*如果当前运算符优先级比栈顶优先级高,那么直接压入s1*/ 31 s1.push(item); 32 break; 33 } else {/*否则将s1栈顶的运算符取出并压入s2,然后继续循环*/ 34 s2.push(s1.pop()); 35 } 36 } 37 } 38 } else {/*不是数字不是运算符就是括号了*/ 39 /* 40 * 5、遇到括号时: 41 5-1. 如果是左括号“(”,则直接压入s1 42 5-2. 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃 43 * */ 44 if (item.equals("(")) { 45 s1.push(item); 46 } else { 47 /*这里就是右括号了*/ 48 /*直到遇到左括号就不操作了,然后再把左括号出来,不忘判空*/ 49 if (!s1.isEmpty()) { 50 while (true) { 51 if (s1.isEmpty() || s1.peek().equals("(")) { 52 break; 53 } else { 54 s2.push(s1.pop()); 55 } 56 } 57 s1.pop(); 58 } 59 } 60 } 61 } 62 /*7、将s1中剩余放入s2*/ 63 while (!s1.isEmpty()) { 64 s2.push(s1.pop()); 65 } 66 /*8、依次输出s2中的元素,并逆序然后返回*/ 67 List<String> temp = new ArrayList<>(); 68 while (!s2.isEmpty()) { 69 temp.add(s2.pop()); 70 } 71 /*然后逆序*/ 72 List<String> result = new ArrayList<>(); 73 for (int i = temp.size() - 1; i >= 0; i--) { 74 result.add(temp.get(i)); 75 } 76 return result; 77 }
4-4-4、源码

1 package t5; 2 3 import com.sun.jndi.ldap.Ber; 4 5 import java.util.ArrayList; 6 import java.util.Arrays; 7 import java.util.List; 8 import java.util.Stack; 9 10 /** 11 * @author 自在仙 12 * @create 2020年04月28 08:38 13 * 逆波兰计算器 14 */ 15 public class ReversePolishNotaion { 16 public static void main(String[] args) { 17 /*String suffixExpression = "1 2 3 + 4 * + 5 -"; 18 19 int calculate = calculate(suffixExpression); 20 System.out.println(calculate);*/ 21 22 List<String> list = expressionSplitToList("9+(3-1)*3+10/2"); 23 24 System.out.println(calculateForList(infixExpressionToToSuffixExpression(list))); 25 } 26 27 /*将一个中缀表达式转换为后缀表达式*/ 28 public static List<String> infixExpressionToToSuffixExpression(List<String> infixExpression) { 29 /*1、初始化两个栈,运算符s1和存储中间结果的s2*/ 30 /*运算符s1*/ 31 Stack<String> s1 = new Stack<>(); 32 /*中间结果s2*/ 33 Stack<String> s2 = new Stack<>(); 34 35 for (int i = 0; i < infixExpression.size(); i++) { 36 /*2、从左到右遍历*/ 37 String item = infixExpression.get(i); 38 /*3、遇到操作数的时候,将其压入s2*/ 39 /*判断是否为数字*/ 40 if (item.matches("\\d+")) { 41 s2.push(item); 42 } else if (isOperator(item)) {/*4、判断是否为运算符*/ 43 /*4-1、如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;*/ 44 while (true) { 45 /*s1为空或者栈顶为左括号*/ 46 if (s1.isEmpty() || s1.peek().equals("(")) { 47 s1.push(item); 48 break; 49 } else { 50 /* 4-2.否则,若优先级比栈顶运算符的高,也将运算符压入s1; 51 4-3.否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4.1)与s1中新的栈顶运算符相比较;*/ 52 /*拿到栈顶和当前运算符的优先级*/ 53 String s1Top = s1.peek(); 54 int t1TopValue = getOperatorPriorityValue(s1Top); 55 int itemValue = getOperatorPriorityValue(item); 56 if (itemValue > t1TopValue) {/*如果当前运算符优先级比栈顶优先级高,那么直接压入s1*/ 57 s1.push(item); 58 break; 59 } else {/*否则将s1栈顶的运算符取出并压入s2,然后继续循环*/ 60 s2.push(s1.pop()); 61 } 62 } 63 } 64 } else {/*不是数字不是运算符就是括号了*/ 65 /* 66 * 5、遇到括号时: 67 5-1. 如果是左括号“(”,则直接压入s1 68 5-2. 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃 69 * */ 70 if (item.equals("(")) { 71 s1.push(item); 72 } else { 73 /*这里就是右括号了*/ 74 /*直到遇到左括号就不操作了,然后再把左括号出来,不忘判空*/ 75 if (!s1.isEmpty()) { 76 while (true) { 77 if (s1.isEmpty() || s1.peek().equals("(")) { 78 break; 79 } else { 80 s2.push(s1.pop()); 81 } 82 } 83 s1.pop(); 84 } 85 } 86 } 87 } 88 /*7、将s1中剩余放入s2*/ 89 while (!s1.isEmpty()) { 90 s2.push(s1.pop()); 91 } 92 /*8、依次输出s2中的元素,并逆序然后返回*/ 93 List<String> temp = new ArrayList<>(); 94 while (!s2.isEmpty()) { 95 temp.add(s2.pop()); 96 } 97 /*然后逆序*/ 98 List<String> result = new ArrayList<>(); 99 for (int i = temp.size() - 1; i >= 0; i--) { 100 result.add(temp.get(i)); 101 } 102 return result; 103 } 104 105 /*将表达式拆分到集合*/ 106 public static List<String> expressionSplitToList(String expression) { 107 /*1、先将表达式拆分到一个List中*/ 108 List<String> infixExpressionList = new ArrayList<>(); 109 int index = 0; 110 String temp = ""; 111 while (true) { 112 String item = expression.charAt(index) + ""; 113 /*如果为数字,那么判断是否还有多位*/ 114 if (item.matches("\\d+")) { 115 while (true) { 116 /*判断是否为最后一位*/ 117 if (index != expression.length() - 1) { 118 /*判断后面是否为数字*/ 119 if ((expression.charAt(index + 1) + "").matches("\\d+")) { 120 item += expression.charAt(++index) + ""; 121 } else { 122 break; 123 } 124 } else { 125 break; 126 } 127 } 128 infixExpressionList.add(item); 129 } else { 130 /*否则就直接加入*/ 131 infixExpressionList.add(item); 132 } 133 /*结束*/ 134 if (index == expression.length() - 1) { 135 break; 136 } 137 /*否则叠加*/ 138 index++; 139 } 140 return infixExpressionList; 141 142 } 143 144 /** 145 * 逆波兰计算器 146 * 传入后缀表达式字符串,返回计算结果 147 * 148 * @param suffixExpression 后缀表达式字符串 149 * @return 150 */ 151 public static int calculateForString(String suffixExpression) { 152 return calculateForStringArray(suffixExpression.split(" ")); 153 } 154 155 /** 156 * 逆波兰计算器 157 * 传入后缀表达式拆分后的数组,返回计算结果 158 * 159 * @param suffixExpressionArray 后缀表达式拆分后的数组 160 * @return 161 */ 162 public static int calculateForStringArray(String[] suffixExpressionArray) { 163 ArrayList<String> strings = new ArrayList<>(); 164 for (int i = 0; i < suffixExpressionArray.length; i++) { 165 strings.add(suffixExpressionArray[i]); 166 } 167 return calculateForList(strings); 168 } 169 170 /** 171 * 逆波兰计算器 172 * 传入后缀表达式字符串,返回计算结果 173 * 174 * @param suffixExpressionList 后缀表达式拆分后的集合 175 * @return 176 */ 177 public static int calculateForList(List<String> suffixExpressionList) { 178 /* 179 * 从左至右扫描表达式, 180 * 遇到数字时,将数字压入堆栈, 181 * 遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈; 182 * 重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果 183 * */ 184 /*先创建一个栈,用来存放数字*/ 185 Stack<Integer> numStack = new Stack<>(); 186 for (String item : suffixExpressionList) { 187 /*判断是不是数字,如果是数字,直接入栈*/ 188 if (item.matches("\\d+")) { 189 numStack.push(Integer.valueOf(item)); 190 } else { 191 /*两个数*/ 192 Integer num1 = numStack.pop(); 193 Integer num2 = numStack.pop(); 194 /*如果是符号,那么从栈中拿两个数然后计算后并放回栈中*/ 195 switch (item) { 196 case "+": 197 numStack.push(num1 + num2); 198 break; 199 case "-": 200 numStack.push(num2 - num1); 201 break; 202 case "*": 203 numStack.push(num1 * num2); 204 break; 205 case "/": 206 numStack.push(num2 / num1); 207 break; 208 default: 209 throw new RuntimeException("操作符错误!"); 210 } 211 } 212 } 213 return numStack.pop(); 214 } 215 216 /** 217 * 判断是否为运算符 218 * 219 * @param value string 220 * @return 是否为运算符 + - * / 221 */ 222 public static boolean isOperator(String value) { 223 return "+".equals(value) || "-".equals(value) || "*".equals(value) || "/".equals(value); 224 } 225 226 /** 227 * 获取运算符优先级 228 * 229 * @param operator 230 * @return +|- 1 *|/ 2 否则0 231 */ 232 public static int getOperatorPriorityValue(String operator) { 233 switch (operator) { 234 case "+": 235 case "-": 236 return 1; 237 case "*": 238 case "/": 239 return 2; 240 default: 241 return 0; 242 } 243 } 244 }
学艺不精,表达不明,还望谅解




