webgl圈中物体

这篇的标题非常不符合我的气质！

注意标题中有个“圏” 字 并不是“选”

下面的圈中物体解决方案 其实已经把如何选中一个物体的问题一并搞定了

圈中物体 首先要有一条封闭曲线吧 那条曲线是由n个线段拼接起来的 我们要找到相交的那两条线段和那两条线段之间的所有线段 如图

 

相交的线段就是这两了 封闭曲线的起始和结束线段就是它们 不过还得截取它们的头或尾 绿色线段起始坐标替换为交点坐标  蓝色线段结束坐标替换为交点坐标

那么如何解决线段相交呢？

有好几种解决方案 我这里提供一种是利用直线参数式来解的 如下

p01=p0+v0*t

p11=p1+v1*s 

p0x+v0x*t=p1x+v1x*s

p0y+v0y*t=p1y+v1y*s

可以使用消元法来解 s 和 t 也可以使用 canvas曲线面片1 那种矩阵方法来解

如果 s和t同时大于0并且小于1  说明相交了 把s和t带进去可以计算出交点了

相交代码

Miku.lineCross = function(l1,l2){
      var t1,t2;
      var [v1,v2] = [
        new Miku.Vec(l1.x2-l1.x1 , l1.y2-l1.y1)
        ,new Miku.Vec(l2.x2-l2.x1 , l2.y2-l2.y1)
      ]
      const ar = [
        [v1.x,-v2.x]
        ,[v1.y,-v2.y]
      ];
      const res = Miku.Det2( ar , [l2.x1-l1.x1 , l2.y1-l1.y1]  );

      if(!res) return {cross:0};

      t1 = res[0],t2 = res[1];
      const o = {cross:t1>0&&t1<1&&t2>0&&t2<1,pos:0};
      if(o.cross){
        return o.pos = {
          x : l1.x1 + v1.x*t1
          ,y:l1.y1 + v1.y*t1
          ,xx:l2.x1 + v2.x*t2
          ,yy:l2.y1 + v2.y*t2
        }
        ,o;
      }
      return o;
    }

 

接下来要解决物体是不是被圈了

物体就是个任意多边形 所以你可以想到与多边形的边来做相交处理是吧。。然而并不能满足所有情况

如果曲线包含了整个物体 但是它没有与任何边相交也算被圈中 又或者曲线全包含在物体内呢？

所以要换种方法了 我这里提供一种叫环绕数的解决方案 如下

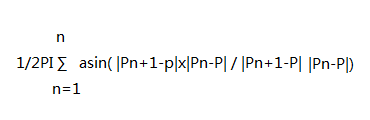
想象在上图那个封闭曲线内有一点P Pn是线段的端点 P的环绕数就可通过这个式子给出 如果结果是+-1  那就在内部

其实还可以用点乘给出结果 不过据我观察仅适用于凸边形。。

另种情况就是曲线全部在物体内部 那么Pn就是物体的顶点 反过来处理一变。。

环绕数代码（具体的可看后面给的源码）

for(let i = 0,dot;dot = ar[i++];){
  let n = 0;
  for(let j =0,l;l = this.cross_ar[j++];){
    let v1 = (new Miku.Vec(l.x1-dot.x , l.y1-dot.y)).normal();
    let v2 = (new Miku.Vec(l.x2-dot.x , l.y2-dot.y)).normal();
    n += asin(v1.cross(v2))*v;
  }
if(f(abs(n))) return 1;
}

这两关键问题就解决了

不过还要注意 这里用的是webgl接口 所以鼠标坐标还要规范下 代码

Miku(c).on('touchmove',e=>{
    var [x,y] = [(e.mouse_x-c.cx)/c.cx , -(e.mouse_y-c.cy)/c.cy];
    Xline.setRoute({x,y});
  });

cx cy是中心位置  xy值-1到1

 

给个 demo