[北京省选集训2019]图的难题
很显然假如存在一个合法的染色方案,染色后黑色边和白色边分别会形成两片森林(毕竟不存在环)。那么什么时候是不合法的呢?考虑下面这张图:
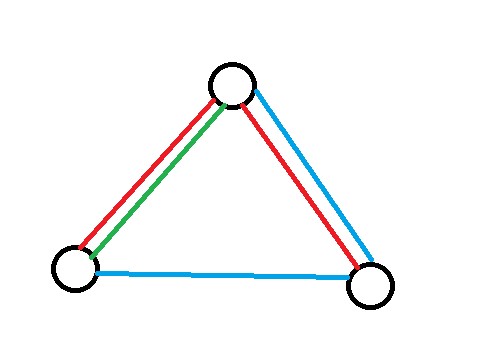
假如红色是白边,蓝色是黑边(黑色和白色不好看……),此时红色和蓝色已经分别形成了两片森林(虽然是独木成林)。这时候我们加入了一条绿色的边,尴尬地发现无论它被染成什么颜色都会形成环。此时思考一下什么样的边才可能陷入绿色边那样的尴尬处境呢?那就是它连接的两个点在两种颜色的森林里都在一棵树上(有点绕理解一下)。假设我们之前一直秉承着不让别人尴尬的原则尽量避免绿色边这样的情况出现,那么出现绿边时一定是无可救药的状态,也就是说两种颜色的森林里对应的两棵树的交集一定是包含两个点之间的一棵子树(因为前面的选择已经尽量避免尴尬情况的出现了。可能有点绕?画个图可能会好点)。
现在我们把这两棵树提取出来,假设当前树上挂着 \(N\) 个点,根据树的边点数量关系在原图中它们已经被选择了 \(2\times(N-1)\) 条边,由于这条绿边的存在这个子图内就存在着多于 \(2\times(N-1)\) 条边啦。总结一下,出现绿边当且仅当原图有一个子图的边数多于点数二倍减二。也就是说,问题就变成了判定是否有一个子图不符合上面的条件。
写个柿子: \(|E|\le 2|V|-2\) 即是 \(|E|-2|V|\le -2\) 。感觉有点熟悉,再一看发现,由于选了一条边就意味着选择两个点,所以可以看成是这两个点是这条边的后继,这样一来一个子图就变成了一些边和它们的后继的并集。一些元素和它们的后继?这不就是闭合子图嘛。而证明一些子图都小于某个值就证明最大的小于那个值就可以啦。于是就是最大权闭合子图问题了。推荐先做 模板题 ,里面有对这个问题的详细阐述,这里就不多言了。
总结做法,对每个点和每条边当成是一个结点,每条边往对应的两个点连无限边,源点向每条边连 \(1\) 边,每个点向汇点连 \(2\) 边,跑网络流即可。然后你会发现过不了样例。这是因为程序认为空集也是一个闭合子图,而它的点权和(也就是 \(0\) )也的的确确是最小的。解决的方法就是枚举强制选择一条边,这样就可以搞出答案了。
代码比较好写。
#include<bits/stdc++.h>
//#define feyn
#define int long long
const int N=5010;
const int M=3e6;
const int maxn=1e12;
using namespace std;
inline void read(int &wh){
wh=0;int f=1;char w=getchar();
while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
while(w>='0'&&w<='9'){wh=wh*10+w-'0';w=getchar();}
wh*=f;return;
}
inline int min(int s1,int s2){
return s1<s2?s1:s2;
}
inline int max(int s1,int s2){
return s1<s2?s2:s1;
}
struct edge{
int t,v,next;
}e[M],se[M];
int head[N],esum;
inline void adde(int fr,int to,int val){
e[++esum]=(edge){to,val,head[fr]};head[fr]=esum;
}
inline void add(int fr,int to,int val){
adde(fr,to,val);adde(to,fr,0);
}
int m,n,cnt,a[N],b[N],ss,tt;
int nt,t[N],q[N],ll,rr,d[N];
inline bool check(){
t[ss]=++nt;d[q[ll=rr=1]=ss]=1;
while(ll<=rr){
int wh=q[ll++];
for(int i=head[wh],th;i;i=e[i].next){
if(e[i].v==0||t[th=e[i].t]==nt)continue;
t[th]=nt;d[th]=d[wh]+1;q[++rr]=th;
}
}
return t[tt]==nt;
}
inline int dinic(int wh,int val){
if(wh==tt)return val;
int used=0;
for(int i=head[wh],th;i;i=e[i].next){
if(e[i].v==0||d[th=e[i].t]!=d[wh]+1)continue;
int now=dinic(th,min(val,e[i].v));
if(now)val-=now,used+=now,e[i].v-=now,e[i^1].v+=now;
if(val==0)break;
}
if(val)d[wh]=-1;return used;
}
void solve(){
cnt=0;esum=1;memset(head,0,sizeof(head));
read(m);read(n);ss=++cnt,tt=++cnt;
for(int i=1;i<=n;i++){a[i]=++cnt;add(ss,a[i],1);}
for(int i=1;i<=m;i++){b[i]=++cnt;add(b[i],tt,2);}
int s1,s2;
for(int i=1;i<=n;i++){
read(s1);read(s2);
add(a[i],b[s1],maxn);
add(a[i],b[s2],maxn);
}
for(int i=1;i<=esum;i++)se[i]=e[i];
int ans=-maxn;
for(int i=1;i<=n;i++){
int an=0;
for(int j=1;j<=esum;j++){
e[j]=se[j];
if(e[j].t==a[i]&&e[j].v==1)e[j].v=maxn;
}
while(check())an+=dinic(ss,maxn);
ans=max(ans,n-an);
}
if(ans<=-2)printf("Yes\n");
else printf("No\n");
}
signed main(){
#ifdef feyn
freopen("in.txt","r",stdin);
#endif
int T;read(T);
while(T--)solve();
return 0;
}


