摩天大楼 题解

link

loj又有好东西啦。

想到从小到大一个一个插入元素进行DP，但问题在于插入那个元素之后对值有多大影响并不好求，毕竟你只维护了极长连续段的个数，并没有维护每个段的首尾有哪些数，所以变化量是无法求的。有一个处理变化量上的核心思想。放张自己用画图造出来的图：

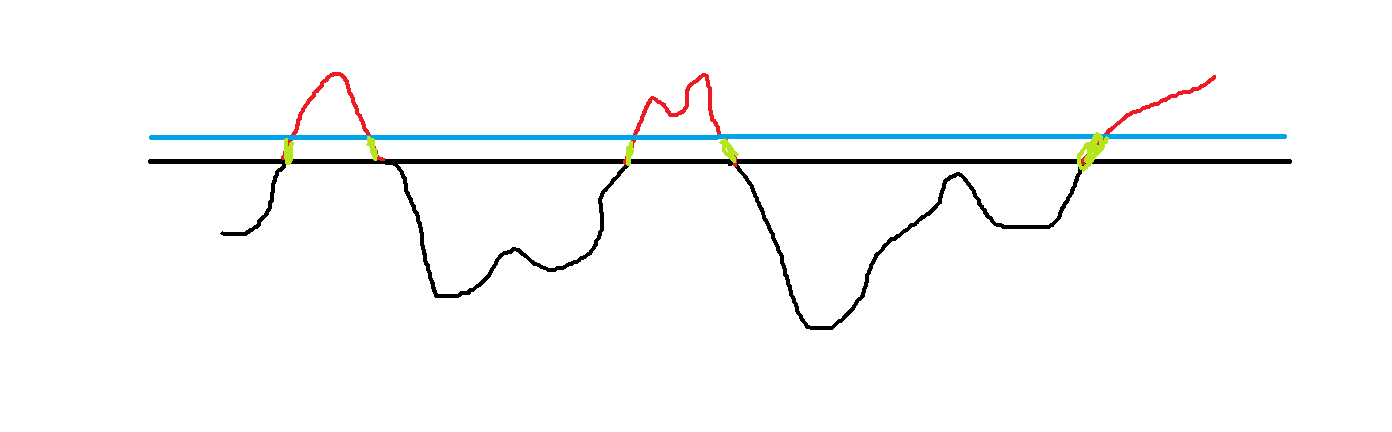
假如把那些数抽象地看成许多点，那么整个序列可以抽象地看成一条曲线。如图，黑线部分是我们已经求得的，蓝水平线是我们这次放进去的数，黑水平线是我们上次放进去的数。会发现曲线长度的变化量是绿线部分，而每条绿线的长度都会等于这次放入的元素和上次的元素的差值，而绿线的条数相当于是黑线部分的非两端的端点数。明白了这一点就可以求了。

用 \(f[i][j][k][h]\) 代表已经放了前i小的数，已经形成了j个极长连续段，这些段中又有h个端点（方便后续统计以及明确状态），然后总的开销是刚好是k的方案总数。于是第i+1个数放的不同位置就对应了不同的决策，这一切就变得明朗起来了。

• 放在段和段之间且不和之前的段有来往，有 \(j+1-h\) 种情况，对应 add(f[next][j+1][w][h],data*(j+1-h));
• 放在段和段之前但和某个段融合，此时段的数量不会增加，有 \(2\times j-h\) 种可能的融合点，对应add(f[next][j][w][h],data*(2*j-h));
• 放在两段之间，顺便把两段融合成为一段，段数减一，对应 add(f[next][j-1][w][h],data*(j-1));
• 放在两边形成边界，使得h的值发生改变。在这样的背景下再以是否使段数增加作为分类依据分成两类，分别对应 add(f[next][j+1][w][h+1],data*(2-h)); 和 add(f[next][j][w][h+1],data*(2-h));

可以滚掉一维节省空间。

还有就是 \(f[1][1][0][1]\) 的初值是2，因为边界可能在左也可能在右。调了好久。

#include<bits/stdc++.h>
//#define zczc
#define int long long
using namespace std;
const int mod=1e9+7;
const int N=110;
const int M=1010;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar();}
    wh*=f;return;
}

inline void add(int &s1,int s2){
	s1+=s2;s1%=mod;
}
int m,n,a[N],f[2][N][M][3];

signed main(){
	
	#ifdef zczc
	freopen("in.txt","r",stdin);
	#endif
	
	read(m);read(n);
	if(m==1){
		printf("1");
		return 0;
	}
	for(int i=1;i<=m;i++)read(a[i]);
	sort(a+1,a+m+1);
	f[1][1][0][0]=1;f[1][1][0][1]=2;
	for(int i=1;i<m;i++){
		int now=i&1,next=i+1&1;
		memset(f[next],0,sizeof(f[next]));
		for(int j=1;j<=i;j++){
			for(int k=0;k<=n;k++){
				for(int h=0;h<3;h++){
					int data=f[now][j][k][h];
					if(data==0)continue;
					int w=k+(a[i+1]-a[i])*(j*2-h);
					if(w>n)continue;
					add(f[next][j+1][w][h],data*(j+1-h));
					add(f[next][j-1][w][h],data*(j-1));
					add(f[next][j][w][h],data*(2*j-h));
					if(h<2)add(f[next][j+1][w][h+1],data*(2-h));
					if(h<2)add(f[next][j][w][h+1],data*(2-h));
				}
			}
		}
	}
	int ans=0,fl=m&1;
	for(int i=0;i<=n;i++)add(ans,f[fl][1][i][2]);
	printf("%lld",ans);
	
	return 0;
}