[ZJOI2007]棋盘制作

link

一种名为垂线DP的……奇怪方法？

这是在题解区找到的一种命名奇怪的、针对一类矩形最值问题的求解方法，其实思想非常简单。读完题就大概知道它应该怎么求解，但很明显这种奇怪的东西写起来要简洁许多。

这道题的题意就是希望找到一个最大的矩形，满足格子黑白相间。说一下“垂线DP”的基本思路吧：

很明显可以考虑贡献点。一个显然的结论就是任何矩形都会有个下边，那么可以考虑在这个下边的某一个点上进行更新。它的考虑就是贪心地向上尽量延续，使得矩形竖直方向最长的同时横向宽度取最小值。这样我们就需要考虑它的正确性，首先它可能是错误的，当且仅当有矩形和它底的位置相同，高度比它小但是宽度比它大，像这样：

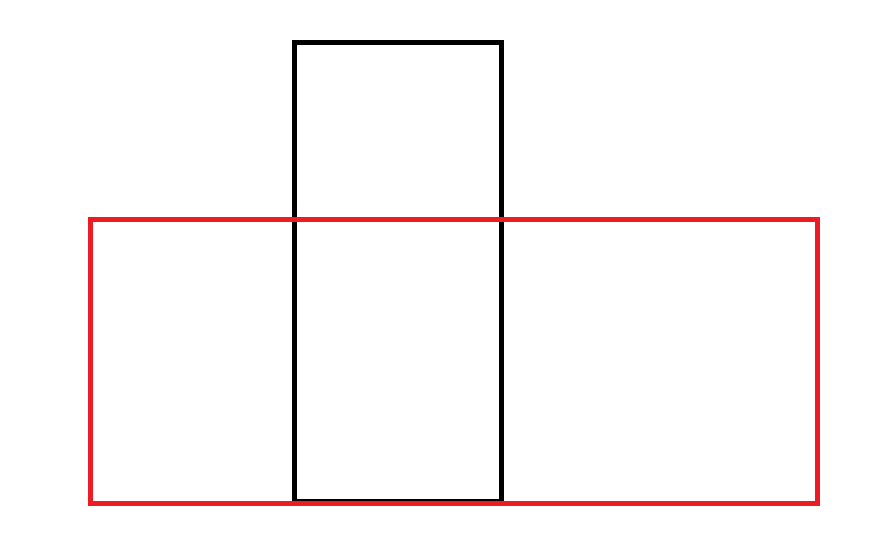
红色为实际上的更优矩形，黑色是我们找到的矩形。不得不承认这种情况确实可以影响正确性，但是我们发现在红色矩形的左下角或者右下角实际上是可以更新出正确答案的。于是乎就证明了该方法的正确性。

code:

#include<cstdio>
//#define zczc
const int N=2010; 
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar();}
    wh*=f;return;
}
inline int max(int s1,int s2){
	return s1<s2?s2:s1;
}
inline int min(int s1,int s2){
	return s1<s2?s1:s2;
} 

int m,n,a1,a2,a[N][N],r[N][N],l[N][N],u[N][N];

signed main(){
	
	#ifdef zczc
	freopen("in.txt","r",stdin);
	#endif
	
	read(m);read(n);
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			read(a[i][j]);
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			l[i][j]=max(a[i][j]==a[i][j-1]?0:l[i][j-1]+1,1);
	for(int i=1;i<=m;i++)
		for(int j=n;j;j--)
			r[i][j]=max(a[i][j]==a[i][j+1]?0:r[i][j+1]+1,1);
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++){
			u[i][j]=1;
			if(a[i][j]^a[i-1][j]){
				u[i][j]=u[i-1][j]+1;
				l[i][j]=min(l[i][j],l[i-1][j]);
				r[i][j]=min(r[i][j],r[i-1][j]);
			}
			int s1=u[i][j],s2=r[i][j]+l[i][j]-1;
			a1=max(a1,s1*s2);
			a2=max(a2,min(s1,s2)*min(s1,s2));
		}
	}
	printf("%d\n%d",a2,a1);
	
	return 0;
}