牛牛的滑动窗口
题面
链接：https://ac.nowcoder.com/acm/contest/7604/D
牛牛最近学习了滑动窗口类的算法，滑动窗口算法可以解决一些线性数组的离线静态区间查询类问题。
具体来说，假设对于一个数组进行m次静态区间查询问题。如果这些查询满足条件：\(\forall i,j\)当\(l_i\le l_j\)时，一定满足\(r_i\le r_j\)（i,j表示查询的编号，l,r表示查询的左右端点）
接下来只要查询的问题满足可以快速插入和删除单点，就可以使用滑动窗口优化，将这m次查询的复杂度降低到O(n)。
牛牛接下来想要问你的问题也和定长滑动窗口有关。
众所周知，长度为k的滑动窗口从左到右去截取一个长度大小为n的数组时，一共可以截取到n-k+1个子数组。
牛牛将这n-k+1个子数组的极大值与极小值的乘积求和称为该数组的"第k窗口值"。
举个例子，假设长度为5的数组为[1,5,2,4,3]，长度为3的滑动窗口可以截取三个子数组，它们分别为[1,5,2],[5,2,4],[2,4,3]。
所以该数组的“第3窗口值”为1*5+2*5+2*4=23。
对于一个给定大小的数组n，牛牛现在想要知道它的第1,2,3,4,5...n窗口值各是多少，请你编写程序解决他的问题。
\(1\le n\le 10^5,1\le a_i \le 10^2\)
解法
朴素的算法就是用单调队列\(O(N)\)模拟每个区间长度下的值之和，算法\(O(N^2)\)。
但很显然这个算法过不了，原因在于\(a_i\)很小，这就意味着能取到的贡献值不会超过\(10^4\)，这也意味着有很多区间其实它们的值是一样的。
比如样例
5
1 5 2 4 3
可以发现区间[1 5]、[1 5 2]、[1 5 2 4]、[1 5 2 4 3]它们的贡献都是\(1\times 5=5\)，而朴素算法把它们都算了一遍，事实上我们只需要给区间长度在2和5之间的位置加上5，也可以达到同样的效果。
于是想到先固定左端点，然后再统计一些右端点的答案。
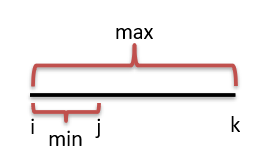
假如当前固定左端点为i，而i后面第一个比\(a_i\)大的位置在k，第一个比它小的位置在j，那么\(max(a_s)=a_i,s\in[i,k-1]\)，同理\(min(a_s)=a_i,s\in[i,j-1]\)。那么很明显，所有以i为左端点、\(r(r\in [j-1,k-1])\)为右端点的区间所产生的贡献都是\(a_i\times a_i\)，换言之，所有长度为\(len(len\in[1,min(j-i,k-i)])\)的答案都应该加上\(a_i\times a_i\)。
然后继续往后扫描，重复比较即可。
#include<cstdio>
#include<stack>
#define ll long long
//#define zczc
using namespace std;
const int N=100010;
inline void read(int &wh){
wh=0;int f=1;char w=getchar();
while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
wh*=f;return;
}
inline int min(int s1,int s2){
return s1<s2?s1:s2;
}
inline int max(int s1,int s2){
return s1<s2?s2:s1;
}
int m,a[N];
#define lowbit (wh&-wh)
ll t[N];
inline void ch(int wh,ll val){
for(;wh<=m;wh+=lowbit)t[wh]+=val;
}
inline void change(int l,int r,ll val){
//printf("change:%d %d %lld\n",l,r,val);
ch(l,val);ch(r+1,-val);return;
}
inline ll work(int wh){
ll an=0;
for(;wh;wh-=lowbit)an+=t[wh];
return an;
}
#undef lowbit
struct node{
int num,data;
};
stack<node>st;
int firmin[N],firmax[N];
signed main(){
#ifdef zczc
freopen("in.txt","r",stdin);
#endif
read(m);
for(int i=1;i<=m;i++)read(a[i]);
firmin[m+1]=firmax[m+1]=m+1;
st.push((node){m+1,101});
for(int i=m;i;i--){
while(st.top().data<=a[i])st.pop();
firmax[i]=st.top().num;
st.push((node){i,a[i]});
}
while(!st.empty())st.pop();
st.push((node){m+1,0});
for(int i=m;i;i--){
while(st.top().data>=a[i])st.pop();
firmin[i]=st.top().num;
st.push((node){i,a[i]});
}
for(int i=1;i<=m;i++){
int nl=i,lmax=firmax[i],lmin=firmin[i],nmax=a[i],nmin=a[i];
while(nl<=m){
change(nl-i+1,min(lmax,lmin)-i,(ll)nmax*nmin);
nl=min(lmax,lmin);
if(lmin<lmax){
nmin=a[lmin];
lmin=firmin[lmin];
}
else{
nmax=a[lmax];
lmax=firmax[lmax];
}
}
}
for(int i=1;i<=m;i++)printf("%lld ",work(i));
return 0;
}
