线段树Ⅰ

很久没写过博客了，特来怀旧一番……

毕竟本人刚学完线段树，也对其有了一些些认知，特来总结一番……

一，基础线段树

就是传说中的线段树，到现在模板已经敲了不下一百遍了（似乎有点夸张欸……），毕竟熟能生巧嘛……

万丈高楼平地起，模板也是要好好写的：

#include<cstdio>
#define int long long
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,a[N];
struct tree1{
	//结构体不管他，就当它不存在 
	#define lc (wh<<1)
	#define rc (wh<<1|1)
	#define mid (t[wh].l+t[wh].r>>1)
	#define num (t[wh].r-t[wh].l+1)
	//define大法好，卡常专用 
	struct node{
		int l,r,data,lazy;
	}t[N*4];
	inline void pushnow(int wh,int val){
		t[wh].lazy+=val;
		t[wh].data+=num*val;
	}
	inline void pushdown(int wh){
		if(t[wh].lazy){
			pushnow(lc,t[wh].lazy);
			pushnow(rc,t[wh].lazy);
			t[wh].lazy=0;
		}
	}
	inline void pushup(int wh){
		t[wh].data=t[lc].data+t[rc].data;
	}
	void build(int wh,int l,int r,int a[]){
		t[wh].l=l,t[wh].r=r;
		if(l==r){
			t[wh].data=a[l];
			t[wh].lazy=0;
			return;
		}
		build(lc,l,mid,a);
		build(rc,mid+1,r,a);
		pushup(wh);
	}
	void change(int wh,int wl,int wr,int val){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			pushnow(wh,val);
			return;
		}
		pushdown(wh);
		if(wl<=mid)change(lc,wl,wr,val);
		if(mid<wr)change(rc,wl,wr,val);
	    pushup(wh);
	}
	int work(int wh,int wl,int wr){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			return t[wh].data;
		}
		pushdown(wh);
		int an=0;
		if(wl<=mid)an+=work(lc,wl,wr);
		if(mid<wr)an+=work(rc,wl,wr);
		pushup(wh);
		return an;
	}
	#undef lc
	#undef rc
	#undef mid
	#undef num
	//模板 
}t1;

signed main(){
	
	int s1,s2,s3,s4;
	read(m);read(n);
	for(int i=1;i<=m;i++)read(a[i]);
	t1.build(1,1,m,a);
	while(n--){
		read(s1);
		if(s1==1){
			read(s2);read(s3);read(s4);
            t1.change(1,s2,s3,s4);			
		}
		else{
			read(s2);read(s3);
			printf("%lld\n",t1.work(1,s2,s3));
		}
	}
	
	return 0;
}

二，多个lazy

只能说线段树和树状数组的关系近似于人和猴子，lazy标记可以约等于是直立行走。因为lazy标记使得线段树可以支持区间修改，功能相较于树状数组要拓展了许多。

lazy不仅仅可以记录区间待加，还可以记录许多许多好东西。做这一部分题，基本上就是列公式，把可以维护的东西用线段树包装起来就可以了

比如说这道题：线段树2

很明显一个lazy标记已经不足以满足膨胀的毒瘤数据的野心了，所以需要加上另外的lazy。这是多个lazy的最基本应用，至少我是这么觉得的。

#include<cstdio>
#define int long long
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,a[N],mod;
struct tree1{
	#define lc (wh<<1)
	#define rc (wh<<1|1)
	#define mid (t[wh].l+t[wh].r>>1)
	#define num (t[wh].r-t[wh].l+1)
	struct node{
		int l,r,data,lazyc,lazyj;
		//lazyj表示加标记，lazyc表示乘标记
		//一段区间的子区间等于 (它们本来的data * lazyc + lazyj)
	}t[N*4];
	inline void pushnow(int wh,int valc,int valj){
		//修改某个区间 
		t[wh].data=(t[wh].data*valc+num*valj)%mod;
		t[wh].lazyj=(t[wh].lazyj*valc+valj)%mod;t[wh].lazyc=t[wh].lazyc*valc%mod;
	}
	//其它函数并木有什么变化…… 
	inline void pushdown(int wh){
		pushnow(lc,t[wh].lazyc,t[wh].lazyj);
		pushnow(rc,t[wh].lazyc,t[wh].lazyj);
		t[wh].lazyc=1,t[wh].lazyj=0;
	}
	inline void pushup(int wh){
		t[wh].data=(t[lc].data+t[rc].data)%mod;
	}
	void build(int wh,int l,int r,int a[]){
		t[wh].l=l,t[wh].r=r,t[wh].lazyc=1;
		if(l==r){
			t[wh].data=a[l];
			return;
		}
		build(lc,l,mid,a);
		build(rc,mid+1,r,a);
		pushup(wh);
	}
	void changec(int wh,int wl,int wr,int val){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			pushnow(wh,val,0);
			return;
		}
		pushdown(wh);
		if(wl<=mid)changec(lc,wl,wr,val);
		if(mid<wr)changec(rc,wl,wr,val);
	    pushup(wh);
	}
	void changej(int wh,int wl,int wr,int val){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			pushnow(wh,1,val);
			return;
		}
		pushdown(wh);
		if(wl<=mid)changej(lc,wl,wr,val);
		if(mid<wr)changej(rc,wl,wr,val);
	    pushup(wh);
	}
	int work(int wh,int wl,int wr){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			return t[wh].data;
		}
		pushdown(wh);
		int an=0;
		if(wl<=mid)an+=work(lc,wl,wr);
		if(mid<wr)an+=work(rc,wl,wr);
		pushup(wh);
		return an%mod;
	}
	#undef lc
	#undef rc
	#undef mid
	#undef num
}t1;

signed main(){
	
	int op,l,r,val;
	read(m);read(n);read(mod);
	for(int i=1;i<=m;i++)read(a[i]);
	t1.build(1,1,m,a);
	while(n--){
		read(op);
		switch(op){
			case 1:
				read(l);read(r);read(val);
				t1.changec(1,l,r,val);
				break;
			case 2:
				read(l);read(r);read(val);
				t1.changej(1,l,r,val);
				break;
			case 3:
				read(l);read(r);
				printf("%lld\n",t1.work(1,l,r)%mod);
				break;
		}
	}
	
	return 0;
}

但是多lazy也有一些比较讨厌的题目，比如这道题：

方差

当年也是调了几个月的代码，却永远都过不了，那绝望的感觉无法言说……最后发现必须要把两个lazy放到同一颗线段树里才能解决问题……

书归正传，这道题就是推公式。

就这样（盗一下图~~~）：

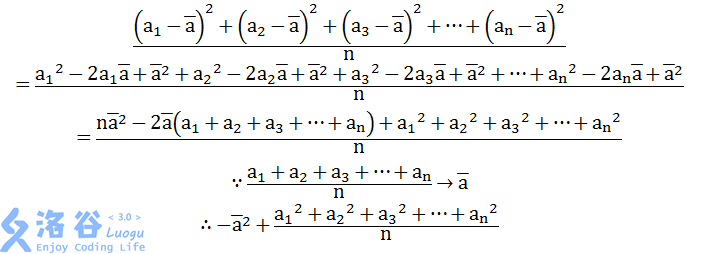
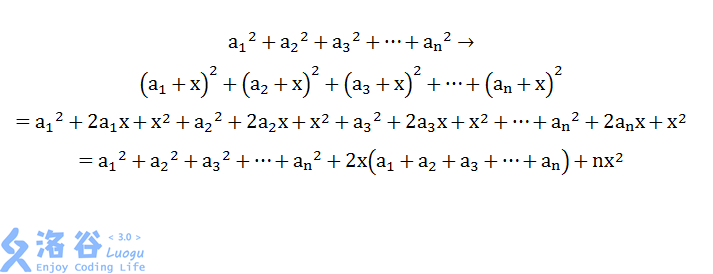
然后就维护就可以啦。当然这道题并不是多lazy，而是一个区间维护多个data（一个区间和一个区间元素平方之和），懒得再写一个部分了，姑且放在多lazy这个部分里。

#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n;
double a[N];
struct tree1{
	#define lc (wh<<1)
	#define rc (wh<<1|1)
	#define mid (t[wh].l+t[wh].r>>1)
	#define num (t[wh].r-t[wh].l+1)
	struct node{
		int l,r;
		double data,data2,lazy;
		//data是区间和，data1是区间平方之和 
		//lazy还是最原始的lazy 
	}t[N*4];
	inline void pushnow(int wh,double val){
		t[wh].lazy+=val;
		t[wh].data2+=t[wh].data*2*val+num*val*val;
		t[wh].data+=num*val;
		//推公式即可 
	}
	inline void pushdown(int wh){
		if(t[wh].lazy!=0){
			pushnow(lc,t[wh].lazy);
			pushnow(rc,t[wh].lazy);
			t[wh].lazy=0;
		}
	}
	inline void pushup(int wh){
		t[wh].data=t[lc].data+t[rc].data;
		t[wh].data2=t[lc].data2+t[rc].data2;
	}
	void build(int wh,int l,int r,double a[]){
		t[wh].l=l,t[wh].r=r;
		if(l==r){
			t[wh].data=a[l];
			t[wh].data2=a[l]*a[l];
			t[wh].lazy=0;
			return;
		}
		build(lc,l,mid,a);
		build(rc,mid+1,r,a);
		pushup(wh);
	}
	void change(int wh,int wl,int wr,double val){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			pushnow(wh,val);
			return;
		}
		pushdown(wh);
		if(wl<=mid)change(lc,wl,wr,val);
		if(mid<wr)change(rc,wl,wr,val);
	    pushup(wh);
	}
	double work1(int wh,int wl,int wr){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			return t[wh].data;
		}
		pushdown(wh);
		double an=0;
		if(wl<=mid)an+=work1(lc,wl,wr);
		if(mid<wr)an+=work1(rc,wl,wr);
		pushup(wh);
		return an;
	}
	double work2(int wh,int wl,int wr){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			return t[wh].data2;
		}
		pushdown(wh);
		double an=0;
		if(wl<=mid)an+=work2(lc,wl,wr);
		if(mid<wr)an+=work2(rc,wl,wr);
		pushup(wh);
		return an;
	}
	#undef lc
	#undef rc
	#undef mid
	#undef num
}t1;

signed main(){
	
	read(m);read(n);
	for(int i=1;i<=m;i++)cin>>a[i];
	t1.build(1,1,m,a);
	int op,wl,wr;
	double val,sum1,sum2,sum3,av;
	while(n--){
		val=sum1=sum2=sum3=av=0;
		read(op);
		switch(op){
			case 1:
				read(wl);read(wr);cin>>val;
				t1.change(1,wl,wr,val);
				break;
			case 2:
				read(wl);read(wr);
				sum1=t1.work1(1,wl,wr);
				printf("%.4f\n",sum1/(wr-wl+1));
				break;
			case 3:
				read(wl);read(wr);
				sum2=t1.work2(1,wl,wr);
				sum1=t1.work1(1,wl,wr);
				av=sum1/(wr-wl+1);
				printf("%.4f\n",sum2/(wr-wl+1)-av*av);
				break;
		}
	}
	
	return 0;
}

三，优雅的暴力

线段树其实也可以暴力去做。如何暴力，就是单点修改啊，这一点在许多不太好加lazy的题里体现出极大的优势。但这样一来线段树的复杂度比线性表还要高，因为它单点修改还要带个log；我们绝不允许这种事发生，就要做到优雅的暴力。

这个部分很灵活，具体题目具体分析。

1，上帝造题的七分钟 2 / 花神游历各国

这道题关键在于：

\(\sqrt 1 = 1\)

知道这一点就够了。

显然区间开方不太好加lazy，那就只能单点修改了；但要做到优雅的暴力，就必须要提前获知这个区间有没有必要进行修改。

在普通的线段树里，如果可以加lazy，那么它的子孙节点便没必要修改；在这道题里，如果一个区间里所有元素都是1，那么这个区间也不会被修改。

所以就可以写了。

另外，由于开方会让数缩小得特别快，一个元素就不会被修改特别特别多次，所以单点修改复杂度也不会炸掉……

#include<cstdio>
#include<cmath>
#define int long long
#define max(s1,s2) ((s1)<(s2)?(s2):(s1))
using namespace std;
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,a[N];

#define lc (wh<<1)
#define rc (wh<<1|1)
#define mid (t[wh].l+t[wh].r>>1)
struct node{
	int l,r,maxn,data;
	//maxn就是区间最大值
	//当然也可以开个bool来记录区间内是否都是1，懒得再去写一遍了 
}t[N*4];
inline void pushup(int wh){
	t[wh].data=t[lc].data+t[rc].data;
	t[wh].maxn=max(t[lc].maxn,t[rc].maxn); 
}
void build(int wh,int l,int r){
	t[wh].l=l;t[wh].r=r;
	if(l==r){
		t[wh].data=t[wh].maxn=a[l];
		return;
	}
	build(lc,l,mid);
	build(rc,mid+1,r);
	pushup(wh);
}
void sq(int wh,int wl,int wr){
	if(t[wh].maxn<=1)return;
	if(t[wh].l==t[wh].r&&wl<=t[wh].l&&t[wh].r<=wr){
		t[wh].data=t[wh].maxn=floor(sqrt(t[wh].maxn));
		return;
	}
	if(wl<=mid)sq(lc,wl,wr);
	if(mid<wr)sq(rc,wl,wr);
	pushup(wh);
}
int work(int wh,int wl,int wr){
	if(wl<=t[wh].l&&t[wh].r<=wr){
		return t[wh].data;
	}
	int an=0;
	if(wl<=mid)an+=work(lc,wl,wr);
	if(mid<wr)an+=work(rc,wl,wr);
	return an;
}
#undef lc
#undef rc
#undef mid
#undef num

signed main(){
	
	read(m);
	for(int i=1;i<=m;i++)read(a[i]);
	read(n);
	build(1,1,m);
	int op,l,r;
	while(n--){
		read(op);
		switch(op){
			case 0:
				read(l);read(r);
				if(l>r){
					int s=l;l=r;r=s;
				}
				sq(1,l,r);
				break;
			case 1:
				read(l);read(r);
				if(l>r){
					int s=l;l=r;r=s;
				}
				printf("%lld\n",work(1,l,r));
				break;
		}
	}
	
	return 0;
}

相似的还有这道题：

The Child and Sequence

一样的，区间取模时数据缩水也会非常快。用相同的思路就可以多水过一道蓝题。

#include<cstdio>
#define int long long
#define max(s1,s2) ((s1)<(s2)?(s2):(s1))
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,a[N];

#define lc (wh<<1)
#define rc (wh<<1|1)
#define mid (t[wh].l+t[wh].r>>1)
#define num (t[wh].r-t[wh].l+1)
struct node{
	int l,r,maxn,data;
}t[N*4];
inline void pushup(int wh){
	t[wh].data=t[lc].data+t[rc].data;
	t[wh].maxn=max(t[lc].maxn,t[rc].maxn); 
}
void build(int wh,int l,int r){
	t[wh].l=l;t[wh].r=r;
	if(l==r){
		t[wh].data=t[wh].maxn=a[l];
		return;
	}
	build(lc,l,mid);
	build(rc,mid+1,r);
	pushup(wh);
}
void change(int wh,int pl,int val){
	if(t[wh].l==t[wh].r&&t[wh].l==pl){
		t[wh].data=t[wh].maxn=val;
		return;
	}
	if(pl<=mid)change(lc,pl,val);
	else change(rc,pl,val);
	pushup(wh);
}
void mod(int wh,int wl,int wr,int val){
	if(t[wh].maxn<val)return;
	if(t[wh].l==t[wh].r&&wl<=t[wh].l&&t[wh].r<=wr){
		t[wh].data=t[wh].maxn=t[wh].maxn%val;
		return;
	}
	if(wl<=mid)mod(lc,wl,wr,val);
	if(mid<wr)mod(rc,wl,wr,val);
	pushup(wh);
}
int work(int wh,int wl,int wr){
	if(wl<=t[wh].l&&t[wh].r<=wr){
		return t[wh].data;
	}
	int an=0;
	if(wl<=mid)an+=work(lc,wl,wr);
	if(mid<wr)an+=work(rc,wl,wr);
	return an;
}
#undef lc
#undef rc
#undef mid
#undef num

signed main(){
	
	read(m);read(n);
	for(int i=1;i<=m;i++)read(a[i]);
	build(1,1,m);
	int op,l,r,val;
	while(n--){
		read(op);
		switch(op){
			case 1:
				read(l);read(r);
				printf("%lld\n",work(1,l,r));
				break;
			case 2:
				read(l);read(r);read(val);
				mod(1,l,r,val);
				break;
			case 3:
				read(l);read(val);
				change(1,l,val);
				break;
		}
	}
	
	return 0;
}

四，和差分擦出的火花

比较考脑子

当然也比较考有没有带够草稿纸。

无聊的数列

硬来。凡是区间修改单点查询都和差分脱不了干系，别问我为什么。硬推总能推出来的。

因为……

如果是区间加单点查询，就可以用差分维护；如果是区间加等差数列，也可以用差分维护。因为假如一个连续的区间，第一个加\(a\)，第二个加\(2a\)，第三个加\(3a\)……反映到差分数组上，差分数组的变化就是这个区间内每一个位置都加上\(a\)。所以可以用线段树来维护。

区间加就可以转化成差分数组的区间加，单点查询可以转化成求差分数组的前缀和，也就是区间查询。线段树都可以解决。

当然这道题没那么简单，有许多细节。

#include<cstdio>
#define int long long
const int N=1e5+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,a[N],b[N];
struct tree1{
	#define lc (wh<<1)
	#define rc (wh<<1|1)
	#define mid (t[wh].l+t[wh].r>>1)
	#define num (t[wh].r-t[wh].l+1)
	struct node{
		int l,r,data,lazy;
	}t[N*4];
	inline void pushnow(int wh,int val){
		t[wh].lazy+=val;
		t[wh].data+=num*val;
	}
	inline void pushdown(int wh){
		if(t[wh].lazy){
			pushnow(lc,t[wh].lazy);
			pushnow(rc,t[wh].lazy);
			t[wh].lazy=0;
		}
	}
	inline void pushup(int wh){
		t[wh].data=t[lc].data+t[rc].data;
	}
	void build(int wh,int l,int r,int a[]){
		t[wh].l=l,t[wh].r=r;
		if(l==r){
			t[wh].data=a[l];
			t[wh].lazy=0;
			return;
		}
		build(lc,l,mid,a);
		build(rc,mid+1,r,a);
		pushup(wh);
	}
	void change(int wh,int wl,int wr,int val){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			pushnow(wh,val);
			return;
		}
		pushdown(wh);
		if(wl<=mid)change(lc,wl,wr,val);
		if(mid<wr)change(rc,wl,wr,val);
	    pushup(wh);
	}
	int work(int wh,int wl,int wr){
		if(wl<=t[wh].l&&t[wh].r<=wr){
			return t[wh].data;
		}
		pushdown(wh);
		int an=0;
		if(wl<=mid)an+=work(lc,wl,wr);
		if(mid<wr)an+=work(rc,wl,wr);
		pushup(wh);
		return an;
	}
	#undef lc
	#undef rc
	#undef mid
	#undef num
}t;

signed main(){
	
	int op,l,r,fir,g;
	read(m);read(n);
	for(int i=1;i<=m;i++)read(a[i]),b[i]=a[i]-a[i-1];
	t.build(1,1,m+1,b);
	while(n--){
		read(op);
		switch(op){
			case 1:
				read(l);read(r);read(fir);read(g);
				t.change(1,l,l,fir);
				t.change(1,r+1,r+1,-fir-g*(r-l));
				t.change(1,l+1,r,g);
				break;
			case 2:
				read(l);
				printf("%d\n",t.work(1,1,l));
				break;
		}
	}
	
	return 0;
}

五，动态开点

虽然暂时还木有什么作用……

但据说像我这种蒟蒻，可以用动态开点解决掉许多平衡树的问题。

【模板】普通平衡树

动态开店代码细节要多一些，流程也要复杂许多：

node数组要开得大一点，一般来说五百万左右，究竟开多大听天由命看数据，空间复杂度比较玄学……
要有个全局变量来记录新节点的编号，再也不能用完全二叉树的方式存储了……
创造新节点时最好是在父节点就写好信息，为什么我也不知道……
如果值域有负数的话一定要这么写：

mid=(l+r>>2)

而不是

mid=(l+r)/2

因为当\(l\)和\(r\)都是负数，且\(r=l+1\)时，\((l+r)/2=r\)，这样如果把\([l,(l+r)/2]\)这个信息带到左儿子里，你会发现左儿子依然会有两个单位长度，这样不就死在里面了吗。但第二种写法就不会有这个问题，我也不知道为什么。

顺便说一句，这是血与泪的教训，当年我调了两个小时，有个点一直MLE，没往这方面想，到最后才发现是\(mid\)写错了导致它无限制地开点，然后就死掉了……

另外，动态开点，每个节点的左右端点有两种写法。一种是记录下来，另一种是递归时生成，两种都可以，没有什么太大的优劣差别。

比如上面那道题的两种写法：

记录在结构体里：

#include<cstdio>
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

#define lc t[wh].left
#define rc t[wh].right
#define mid (t[wh].l+t[wh].r>>1)
struct node{
	int l,r,left,right,data;
}t[3000000];
int cnt=1;
inline void pushup(int wh){
	t[wh].data=t[lc].data+t[rc].data;
}
void change(int wh,int pl,int val){
	if(t[wh].l==t[wh].r){t[wh].data+=val;return;}
	if(pl<=mid){
		if(lc==0){lc=++cnt;t[lc].l=t[wh].l,t[lc].r=mid;}
		change(lc,pl,val);
	}
	else{
		if(rc==0){rc=++cnt;t[rc].l=mid+1,t[rc].r=t[wh].r;}
		change(rc,pl,val);
	}
	pushup(wh);
}
int work(int wh,int wl,int wr){
	if(wh==0)return 0;
	if(wl<=t[wh].l&&t[wh].r<=wr)return t[wh].data;
	int an=0;
	if(wl<=mid)an+=work(lc,wl,wr);
	if(wr>mid)an+=work(rc,wl,wr);
	return an;
}
int find(int wh,int now,int want){
	if(t[wh].l==t[wh].r)return t[wh].l;
	if(now+t[lc].data<want)return find(rc,now+t[lc].data,want);
	else return find(lc,now,want);
}
#undef lc
#undef rc
#undef mid

signed main(){
	
	t[1].l=-1e7,t[1].r=1e7;
	int m,op,x,y;
	read(m);
	while(m--){
		read(op);read(x);
		switch(op){
			case 1:
				change(1,x,1);
				break;
			case 2:
				change(1,x,-1);
				break;
			case 3:
				printf("%d\n",work(1,-1e7,x-1)+1);
				break;
			case 4:
				printf("%d\n",find(1,0,x));
				break;
			case 5:
				y=work(1,-1e7,x-1);
				printf("%d\n",find(1,0,y));
				break;
			case 6:
				y=work(1,-1e7,x);
				printf("%d\n",find(1,0,y+1));
				break;
		}
	}
	
	return 0;
}

递归动态生成：

#include<cstdio>
const int N=1e7+10;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

#define lc t[wh].left
#define rc t[wh].right
#define mid (l+r>>1)
struct node{
	int left,right,data;
}t[100005*40];
int cnt=1;
inline void pushup(int wh){
	t[wh].data=t[lc].data+t[rc].data;
}
void change(int wh,int pl,int val,int l,int r){
	if(l==r){t[wh].data+=val;return;}
	if(pl<=mid){
		if(lc==0)lc=++cnt;
		change(lc,pl,val,l,mid);
	}
	else{
		if(rc==0)rc=++cnt;
		change(rc,pl,val,mid+1,r);
	}
	pushup(wh);
}
int work(int wh,int wl,int wr,int l,int r){
	if(wh==0)return 0;
	if(wl<=l&&r<=wr)return t[wh].data;
	int an=0;
	if(wl<=mid)an+=work(lc,wl,wr,l,mid);
	if(wr>mid)an+=work(rc,wl,wr,mid+1,r);
	return an;
}
int find(int wh,int now,int want,int l,int r){
	if(l==r)return l;
	if(now+t[lc].data<want)return find(rc,now+t[lc].data,want,mid+1,r);
	else return find(lc,now,want,l,mid);
}
#undef lc
#undef rc
#undef mid

signed main(){
	
	int m,op,x,y;
	read(m);
	while(m--){
		read(op);read(x);
		switch(op){
			case 1:
				change(1,x,1,-N,N);
				break;
			case 2:
				change(1,x,-1,-N,N);
				break;
			case 3:
				printf("%d\n",work(1,-N,x-1,-N,N)+1);
				break;
			case 4:
				printf("%d\n",find(1,0,x,-N,N));
				break;
			case 5:
				y=work(1,-1e7,x-1,-N,N);
				printf("%d\n",find(1,0,y,-N,N));
				break;
			case 6:
				y=work(1,-1e7,x,-N,N);
				printf("%d\n",find(1,0,y+1,-N,N));
				break;
		}
	}
	
	return 0;
}

当然动态开点还有许多其它用处，以后再更。

六，离散化

准确来说它并不是线段树的知识点，只是因为它常常用到，也来说一下。

基本知识：离散化

有时区间太大了，而操作时又只需要得到元素之间的大小关系时，就可以用离散化搞定。

另外，在一些题目中，线段树的每一个单位可以是一段区间，而不是一个点。

比如：楼房

如果数据范围比较小的话，可以直接上线段树；但这道题数据范围比较大，就需要离散化的帮助。

#include<cstdio>
#include<algorithm>
#define int long long
#define max(s1,s2) ((s1)<(s2)?(s2):(s1))
using namespace std;
const int N=400010;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,tot,a[N*2],l[N],r[N],h[N];

#define lc (wh<<1)
#define rc (wh<<1|1)
#define mid (t[wh].l+t[wh].r>>1)
struct node{
	int l,r,data;
}t[N*8];
inline void pushup(int wh){
	t[wh].data=max(t[lc].data,t[rc].data);
}
inline void pushnow(int wh,int val){
	t[wh].data=max(t[wh].data,val);
}
inline void pushdown(int wh){
	pushnow(lc,t[wh].data);
	pushnow(rc,t[wh].data);
}
void build(int wh,int l,int r){
	t[wh].l=l,t[wh].r=r;
	if(l==r)return;
	build(lc,l,mid);
	build(rc,mid+1,r);
}
void change(int wh,int wl,int wr,int val){
	if(wl<=t[wh].l&&t[wh].r<=wr){
		pushnow(wh,val);
		return;
	}
	pushdown(wh);
	if(wl<=mid)change(lc,wl,wr,val);
	if(wr>mid)change(rc,wl,wr,val);
	//pushup(wh);
}
int work(int wh,int pl){
	if(t[wh].l==t[wh].r)return t[wh].data;
	pushdown(wh);
	if(pl<=mid)return work(lc,pl);
	else return work(rc,pl);
}
#undef lc
#undef rc
#undef mid

int x[N],y[N],cnt;

signed main(){
	
	read(m);
	for(int i=1;i<=m;i++){
		read(h[i]);read(l[i]);read(r[i]);
		a[++tot]=l[i];a[++tot]=r[i];
	}
	sort(a+1,a+tot+1);
	n=unique(a+1,a+tot+1)-a-1;
	//for(int i=1;i<=n;i++)printf("rg:%d ",a[i]);
	build(1,1,n);
	for(int i=1;i<=m;i++){
		l[i]=lower_bound(a+1,a+n+1,l[i])-a;
		r[i]=lower_bound(a+1,a+n+1,r[i])-a;
		//printf("ch:%d %d %d\n",l[i],r[i]-1,h[i]);
		change(1,l[i],r[i]-1,h[i]);
	}
	int last=0;
	cnt++;
	x[cnt]=a[1],y[cnt]=0;
	for(int i=1;i<n;i++){
		//printf("ag:%d %d\n",i,work(1,i));
		int now=work(1,i);
		if(now!=last){
			++cnt;
			x[cnt]=a[i],y[cnt]=now;
			++cnt;
			x[cnt]=a[i+1],y[cnt]=now;
		}
		else x[cnt]=a[i+1];
		last=now;
	}
	printf("%lld\n",cnt+1);
	for(int i=1;i<=cnt;i++)printf("%lld %lld\n",x[i],y[i]);
	printf("%lld 0\n",a[n]);
	
	return 0;
}

后记

蒟蒻学习线段树不久，总结也只能总结这些了，以后有时间了再回来更新！

学而时习之

undate：

2021.06.06
2021.06.07
2021.06.11

posted @ 2021-08-05 13:51 Feyn618 阅读(38) 评论(0) 编辑收藏举报

刷新页面返回顶部

Feyn's Blog