二分图Ⅰ

啊（我也不知道为什么要加上这个字……），不论如何由于昨天上午没上课（反正从今天开始就改成线上授课了……），这都不重要，反正由于昨天上午比较闲，我决定自学一下之前遗漏的一个知识点，即二分图。

我是看的网上的一篇博客来自学的二分图，虽然啊哈算法里似乎有二分图这个章节，但是我没带过去，这就比较尴尬了……所以，我获得的知识肯定有不完备和不严谨的地方，反正能过题就行了啊……

以下许多内容摘自我昨天学习的博客

1.定义及基本用法

1.1.定义

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。 -------百度百科。

说的好复杂啊， 画个图理解一下。

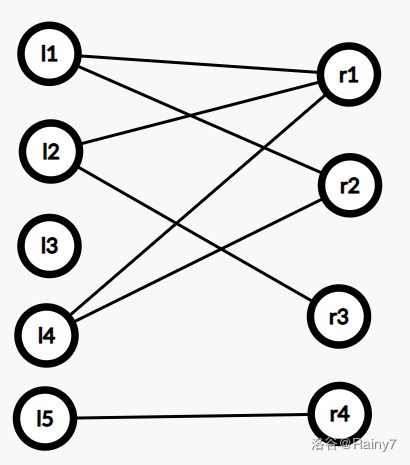
如图，在一个图中，如果能把点分为两个顶点集，使每个集合中，没有两个点有连边。

也就是说，边只会连接两个点集。

1.2.判定

显然，二分图有一个特点，就是要么没有环，要么只偶环。总结一下，当一个图是二分图时，当且仅当它没有奇环。

另外还有一种判定方法，就是感性的判定，如果所有节点都可以分成两个部分，每个部分之内的节点互相没有来往，那它也是一个二分图。比如一个很常用的模型就是国际象棋，它的格子分为黑白格，而骑士永远只能从黑格跳到白格，也就是说黑格和黑格没有联系，白格和白格也没有，所以从某种意义上来说，国际象棋棋盘是一张二分图。

1.3.二分图最大匹配

我只是知道，而且只是模糊地知道它应该怎么写（而且我还只知道匈牙利算法），它的原理和复杂度都比较晕，这也许就是自学的后果吧……

它的思路就是不断找增广路的过程，而且能找多少就找多少，感觉有点像贪心呢……

求二分图最大匹配的一般是用匈牙利算法 ，因为好写。

又是借鉴他人博客：

首先，要先知道一个叫增广路的东西。

若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径（举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行）。 ----百度百科

好复杂啊...？那我们先不管他。

匈牙利算法就是一个不断找增广路的过程，那来手动模拟一下。

(好多人模拟过程都是男女配对啊？？)

比如这个图:

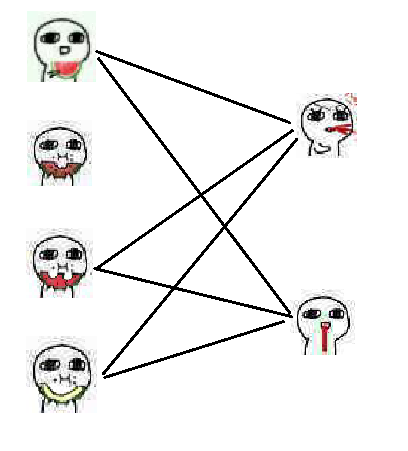
第一次匹配，我们先将第一个吃瓜人匹配到第一个吐血人：

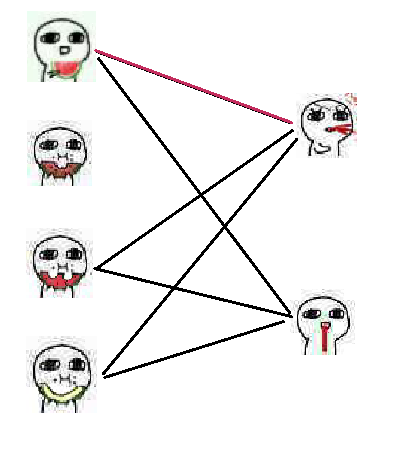
接下来，发现第二个吃瓜人是单着，那不管他了。

第三个吃瓜人，匹配到第一个吐血人，然后发现第一个吃瓜人已经和他匹配了。

那么就去协商一下，第一个吃瓜人发现还能和第二个吐血人匹配，于是第一个吐血人就给了第三个吃瓜人。如图：

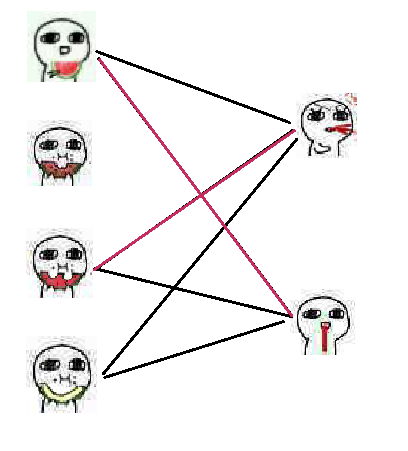
于是轮到了第四个吃瓜人，他想和第一个吐血人匹配，然后发现已经有人匹配了。

于是他和第三个吃瓜人协商， 第三个吃瓜人就选择了第二个吐血人，然后发现已经有人匹配了。

于是第三个吃瓜人去和第一个吃瓜人协商， 第一个吃瓜人选择了第一个吐血人。

结果他发现问题又绕回去了，于是第三个吃瓜人和第一个吃瓜人的协商失败，那么第三个吃瓜人和第四个吃瓜人的协商失败。

也就说，第四个人只能和第二个人一起在旁边吃瓜了。

所以最大匹配数为 \(2\) 。

这大致就是二分图匹配的过程。

而协商过程，其实就是在找增广路。

也就是每个吃瓜人，都是先选择一个未匹配的边，如果对面的点(吐血人)已经被匹配了，那就顺着那个匹配的边找到那个人，那个人再选一个未匹配的边....

复杂度为 \(O(nm)\) 。

反正大概就是这么一个意思。

模板题

#include<cstdio>
#include<cstring>
//#define zczc
using namespace std;
const int N=510;
const int M=50010;
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m,n,num;
struct edge{
	int t,next;
}e[M];
int head[N],esum;
inline void add(int fr,int to){
	esum++;
	e[esum].t=to;
	e[esum].next=head[fr];
	head[fr]=esum;
	return;
}

int a[N];
bool vis[N];
inline bool find(int wh){
	for(int i=head[wh],th;i;i=e[i].next){
		th=e[i].t;
		if(vis[th])continue;
		vis[th]=true;
		if(a[th]==0||find(a[th])){
			a[th]=wh;
			return true;
		}
	}
	return false;
}

signed main(){
	
	#ifdef zczc
	freopen("in.txt","r",stdin);
	#endif
	
	int s1,s2;
	read(m);read(n);read(num);
	for(int i=1;i<=num;i++){
		read(s1);read(s2);
		add(s1,s2);
	}
	
	int ans=0;
	for(int i=1;i<=m;i++){
		memset(vis,false,sizeof(vis));
		if(find(i))ans++;
	}
	printf("%d\n",ans);
	
	return 0;
}

顺便说句题外话，代码里面define了zczc的都是本人的原创代码，反正不论文字部分有多少是借鉴的，代码一定都是本人自己写的~~~

1.4.一些基本结论

灰常重要！！！

Ⅰ 二分图的最小点覆盖=二分图的最大匹配

Ⅱ 二分图中最小边覆盖=顶点数-二分图最大匹配

Ⅲ 二分图的最大独立集 = 总点数-最大匹配数

许多题都要用，一定要记好。

2.一些模板题

飞行员配对问题

太裸了，裸的二分图。

#include<cstdio>
#include<cstring>
//#define zczc
using namespace std;
const int N=110;
const int M=N*N/2;
inline bool get(){
	char w=getchar();
	while(w!='0'&&w!='1')w=getchar();
	return w=='1';
}
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

struct edge{
	int t,next;
}e[M];
int head[N],esum;
inline void add(int fr,int to){
	esum++;
	e[esum].t=to;
	e[esum].next=head[fr];
	head[fr]=esum;
	return;
}

int m,n,a[N];bool vis[N];
inline bool find(int wh){
	for(int i=head[wh],th;i;i=e[i].next){
		th=e[i].t;
		if(vis[th])continue;
		vis[th]=true;
		if(a[th]==0||find(a[th])){
			a[th]=wh;
			return true;
		}
	}
	return false;
}

signed main(){
	
	#ifdef zczc
	freopen("in.txt","r",stdin);
	#endif
	
	int s1,s2;
	read(m);read(n);
	read(s1);read(s2);
	while(s1!=-1){
		add(s1,s2);
		read(s1);read(s2);
	}
	
	int an=0;
	for(int i=1;i<=m;i++){
		memset(vis,false,sizeof(vis));
		if(find(i))an++;
	}
	printf("%d\n",an);
	for(int i=m+1;i<=n;i++){
		if(a[i])printf("%d %d\n",a[i],i);
	}
	
	return 0;
}

还有一些很裸的题，比如假期的宿舍等。

3.一些应用题

攻击装置

顺便说一下，这道题和骑士共存问题是一样的，可以当成一道题来看。

上面说了，国际象棋棋盘是一个天生的二分图，而骑士的移动线路就是天然的连边。最后的答案就是求最大独立点集，就是结论三。套模板即可。

#include<cstdio>
#include<cstring>
#define id(s1,s2) ((s1-1)*m+s2)
//#define zczc
using namespace std;
const int S=210;
const int N=40010;
const int M=N*4;
inline bool get(){
	char w=getchar();
	while(w!='0'&&w!='1')w=getchar();
	return w=='1';
}
inline void read(int &wh){
    wh=0;int f=1;char w=getchar();
    while(w<'0'||w>'9'){if(w=='-')f=-1;w=getchar();}
    while(w<='9'&&w>='0'){wh=wh*10+w-'0';w=getchar(); }
    wh*=f;return;
}

int m;bool c[S][S];
struct edge{
	int t,next;
}e[M];
int head[N],esum;
inline void add(int x1,int y1,int x2,int y2){
	if(x2<1||x2>m||y2<1||y2>m||c[x2][y2])return;
	if(x1<1||x1>m||y1<1||y1>m||c[x1][y1])return;
	int fr=id(x1,y1),to=id(x2,y2);
	esum++;
	e[esum].t=to;
	e[esum].next=head[fr];
	head[fr]=esum;
	return;
}

int a[N];bool vis[N];
inline bool find(int wh){
	for(int i=head[wh],th;i;i=e[i].next){
		th=e[i].t;
		if(vis[th])continue;
		vis[th]=true;
		if(a[th]==0||find(a[th])){
			a[th]=wh;
			return true;
		}
	}
	return false;
}

signed main(){
	
	#ifdef zczc
	freopen("in.txt","r",stdin);
	#endif
	
	int sum=0,fang[4][2]={{-1,-2},{-1,2},{-2,-1},{-2,1}};
	read(m);
	for(int i=1;i<=m;i++){
		for(int j=1;j<=m;j++){
			if(!get()){
		    	for(int k=0;k<4;k++){
		    		add(i,j,i+fang[k][0],j+fang[k][1]);
		    		add(i+fang[k][0],j+fang[k][1],i,j);
		    	}
		    	sum++;
			}
			else c[i][j]=true;
		}
	}
	
	int an=0;
	for(int i=1;i<=m;i++){
		for(int j=1;j<=m;j++){
			if(c[i][j]||(i+j&1))continue;
			memset(vis,false,sizeof(vis));
			if(find(id(i,j)))an++;
		}
	}
	printf("%d\n",sum-an);
	
	return 0;
}

时间不多了，暂且写到这里吧。