平板涂色
题目描述
CE数码公司开发了一种名为自动涂色机(APM)的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。
为了涂色,APM需要使用一组刷子。每个刷子涂一种不同的颜色C。APM拿起一把有颜色C的刷子,并给所有颜色为C且符合下面限制的矩形涂色:
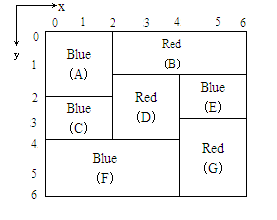
为了避免颜料渗漏使颜色混合,一个矩形只能在所有紧靠它上方的矩形涂色后,才能涂色。例如图中矩形F必须在C和D涂色后才能涂色。注意,每一个矩形必须立刻涂满,不能只涂一部分。
写一个程序求一个使APM拿起刷子次数最少的涂色方案。注意,如果一把刷子被拿起超过一次,则每一次都必须记入总数中。
输入输出格式
输入格式:
第一行为矩形的个数N。下面有N行描述了N个矩形。每个矩形有5个整数描述,左上角的y坐标和x坐标,右下角的y坐标和x坐标,以及预定颜色。
颜色号为1到20的整数。
平板的左上角坐标总是(0, 0)。
坐标的范围是0..99。
N小于16。
输出格式:
文件中记录拿起刷子的最少次数。
输入输出样例
其实这道题就是一道妥妥的深搜,但还有一群大佬用DP,诶(其实我不打DP是因为,我根本就不会⊙﹏⊙),我们发现这道题有一个坑,如果上面没有涂,就要先涂上面的。
代码:
#include<bits/stdc++.h>
using namespace std;
struct str
{
int a1,a2,b1,b2,color;
}a[111000];
int b1[11000]={0};//有没有涂
int b[110][110],n,m,ans=999;
int b2[11000];//颜色数量
int cmp(str x,str y)//排序
{
if(x.a1!=y.a1) return x.a1<y.a1;//在排横列
return x.a2<y.a2;//先排纵列
}
bool cha(int x)
{
for(int i=0;i<n;i++)
{
if(b[x][i]&&!b1[i]) return false;//上面没涂,反回false
}
return true;//反回true
}
void dfs(int x,int ji_lu,int sum)
{
if(x>=ans)//如果当前的值大于你要找的值,那就不用找了呢!O(∩_∩)O~~
{
return ;
}
if(sum==n)//涂完了
{
ans=x;
return ;
}
for(int i=0;i<m;i++)//枚举每一种颜色
{
int h=0;
if(b2[i]&&i!=ji_lu)//可以涂,有颜色涂,没有被涂过
{
for(int j=0;j<n;j++)
{
//cha函数判断上面有没有被涂(颜色)
if(!b1[j]&&a[j].color==i&&cha(j))//如果没涂过,且能涂
{
b1[j]=1;//记录
h++;
}
else if(b1[j]&&a[j].color==i) b1[j]++;
}
if(h>0)//如果被涂了
{
dfs(x+1,i,sum+h);//进行下一步
}
for(int j=n-1;j>=0;j--)//回溯,不能上色
{
if(b1[j]==1&&a[j].color==i&&cha(j))
{
b1[j]=0;
h--;
}
else if(b1[j]>1&&a[j].color==i)
{
b1[j]--;
}
}
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i].a1>>a[i].a2>>a[i].b1>>a[i].b2>>a[i].color;
b2[a[i].color]++;//颜色的数量
}
m=19;//从零开始
sort(a,a+n,cmp);//应为蒟蒻不会拓扑排序所以先排一下
for(int i=1;i<n;i++)
{
for(int j=i-1;j>=0;j--)
{
if(a[i].a1==a[j].b1&&((a[i].a2>=a[j].a2&&a[i].a2<=a[j].b2)||(a[i].b2>=a[j].a2&&a[i].b2<=a[j].b2)))
{
b[i][j]=1;//如果i块的最上面,且紧邻j块最下面,并且两砖横坐标有重叠部分,即i块为j块,紧邻的那块砖
}
}
}
dfs(0,0,0);
cout<<ans;
}
做完之后,我只想去出题人面前说一句话:午时已到。



