文法和语言，理解克林闭包
写在开始：
上篇我们介绍了编译 “工厂” 的流程，本篇介绍，工厂里的 “工具”。
开始教程：
语言和文法？语言我们知道，计算机语言，人类的语言，动物的语言，不同国家的语言，不同种族的语言等等。那神马是文法呢？所谓文法，文，文字，法，规则，法则，法律。组合起来就是，文字的规则。每种语言都有自己的文法，不同的语言有不同的文法。例如我们的中文的文法，用一种规则来定义句子的组成，还拿 “我是中国人” 为例。
我们的个中文句子构造规则：< 主语 >< 谓语 >< 宾语 >< 补语 >< 状语 >。 而英语的句子构造：S十 V 主谓结构 S 十 V 十 F 主系表结构 S 十 V 十 O 主谓宾结构 S 十 V 十 O1 十 O2 主谓双宾结构 S 十 V十 O 十 C 主谓宾补结构说明：S＝主语；V＝谓语；P＝表语；O＝宾语；O1＝间接宾语；O2＝直接宾语；C＝宾语补足语。我们可以看出汉语和英语有不同的编排，不同的规则，这就是文法。
我们这里要说的是编译程序的文法。
书中的文法定义：使用文法作为工具，不仅为了严格地定义句子的结构，也是为了适当条数的规则把语言的全部句子描述出来，可以说文法是以有穷集合刻画无穷集合的工具。
接下来了解一些关于表示文法的一些基本定义：
一些基本定义
符号和符号串：
正如我们学习的 English 是由单词和标点符号构成的，单词又是有字母构成的，计算机语言也是如此，也是由字母和数字等一些基本符号构成的，一个源程序就是一个 “基本符号串”，所以我们开始了解符号和符号串相关的定义。
字母表：
元素的非空有穷集合。不同的语言有他自己不同的字母表，我们的计算机语言字母表就是数字，字母，标点等若干符号了。中文的字母表就是汉字了。
符号串：
字母表的符号组成任何又穷序列的符号串。例如字母表 A={a,b,c} 则由这个字母表组成的符号串包括： {ab,ac,bc,abc,a,b,c}。
有了这些就相当于有了 123456，接下来就是一些运算了，符号串的一些运算了。
连接运算：
eg：x=bay=nanaxy=banana（很简单，连接在一起）
方幂运算：x^0= e ; x^1 = x;.....;（和小学数学的方幂一致）
两个字母表乘积：∑1={0,1},∑2={a,b},∑1∑2 ={0a,0b,1a,1b}；（小学数学结合运算）
∑的正闭包：
∑+=∑∪∑2∪∑3∪∑4∪……
∑的克林闭包（kleene Closure）：
∑*=∑0∪∑+（与正闭包区别哦，这算是新概念）
例如：{0,1}+ = {0，1，00，01，11，000，001，010，011，100，……}
{0,1}* = {ε，0，1，00，01，11，000，001，010，011，100，…}
我们用这些规则将我们的语言形式化：
“我是中国人”：名词:: = 中国人；代词::= 我；动词::= 是；
编译程序的文法把计算机语言形式化的定义：A->b ; 读作：A 定义为 b；或把他说成是一条关于 A的规则（产生式）；
更加规范的定义：
文法 G 的定义：四元组 (Vn，Vt，P，S)
Vn：是非终结符集；
Vt：终结符集；
P：表示一种规则（a->b）ab 表示终结符和非终结符的集合，但 a 中至少包括一个非终结符。Vn，Vt，P 是非空有穷集合。
S：表示开始符，他是一个非终结符，至少要有一条规则在左侧。
那什么是终结符和非终结符呢？规则又是怎样？开始符？
下面来看一个英文句子，以英文句子为例，说说这个过程，幻灯片上的这个例子很适合初学者。
分析句子：The grey wolf will eat the goat .
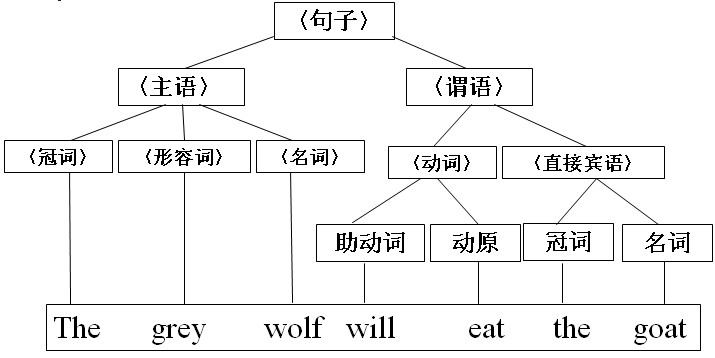
句子的组成规则：
我们如何用文法符号来描述这个归纳的过程呢？这个英文句子怎么形式化的表现出来呢？
这就是为什么我们上述的文法 G 要用那四个符号来表示了：
因为前人发现重复的地方，想用有穷的地方表达无穷的东西，用这四个方式来表示恰好能将所有的句子归纳。
这是对一个句子的分析，当然如果有一个句子，我们也可以根据这种规则判断是个句子是否符合英文的文法。
文法描述的语言是该文法一切句子的集合。
给出几个词，我们能根据文法组成一个句子，可以根据规则产生语言。
给出一个句子，我们把句子的词进行归类，可以判断这个句子是否可被识别。
例如：the grey will eat the goat
the grey wolf will eat wolf
the grey goat will eat the wolf
the grey goat will eat the grey
符合语法语义的句子仅是：
the grey wolf will eat goat
所以文法 G 的形式定义如上所述
Vt：终结符，我们一般用除了大写字母表示。
Vn：非终结符，我们一般用大写字母表示。
S：一般是开始符号。
P：就表示一种规则啦。
a->b 被称为产生式（定义式）
仙人（前人）给定义的一些说法：
文法 G、、上述定义，cd 是 Vn 和 Vt 中任意字符，符号串 V 和 W V=caW=db (规则 a->b) 则 V能直接产生 W，则说 W 是 V 的直接推导。或说 W 直接规约到 V。
1 如果 V->W0->W1->W2...->Wn=W (n>0) 则称 W 规约到 V 记作：V ---+- >W （箭头上带一个加号，写的时候不方便。。）
若 1 或 V=W 则记作 V ---*->W (箭头上带一个星号)
句子句型：
设 G[S] 是以文法，如果符号 x 是从识别符号推到出来的，即有 S---*--->x , 则称 x 是文法 G[S] 的句型。
若 x 仅由终结符号组成，则称 x 为该文法 G[S] 的句子。
