学习hmm近一周的时间，做个总结。
参考 李航的《统计学习方法》第9章，第10章
本文包含：
1.hmm模型
2.前向后向算法
3.Baum-Welch算法
4.维特比算法
1.hmm模型
Q：所有可能的状态的集合（一般是指隐藏状态），N是指可能的状态数
V：所有可能的观测的集合，M是可能的观测数
I：长度为T的状态序列。（一般是指隐藏状态），T是时间
O：对应的观测序列。和I一样的时间T，表明一一对应。
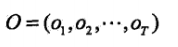
A：状态转移概率矩阵
(A=[a_{ij}]_{N*N})
(a_{ij}=P(i_{t+1}=q_{j}|i_{t}=q_{i}),i=1,2,...,N;j=1,2,...,N)
aij是指时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。（上一时刻状态i，转移到下一时刻状态j的概率）
B：观测概率矩阵
(B=[b_{j}(k)]_{N*M})
(b_{j}(k)=P(o_{t}=v_{k}|i_{t}=q_{j}),k=1,2,...,M;j=1,2,...,N)
bj(k)指在时刻t处于状态qj的条件下，生成观测为vk的概率。（状态为j，生成观测为k的概率）
pai：初始状态概率向量
(\pi =(\pi_{i}))
\pi_{i}=P(i_{1}=q_{i}),i=1,2,...,N
pai(i)时刻t=1处于状态qi的概率。（初始时刻的状态也是不确定的，也可能是各个状态的分布）
hmm模型参数：可由pai，A，B构成，pai和A决定状态序列，B决定观测序列。hmm模型用lambda表示：
(\lambda =(A,B,\pi ))
2.问题一:概率计算问题
给定hmm模型，和观测序列O，计算在模型lambda下观测序列O出现的概率
2.1前向算法
前向概率：给定hmm，定义到时刻 t 观测序列为 {o1,o2...ot}，且状态为qi的概率。
(\alpha _{t}(i)=P(o_{1},o_{2},...,o_{t},i_{t}=q_{i}|\lambda ))
（已知观测序列o，t 时刻状态为 i 的前向概率
）
初值：
递归：
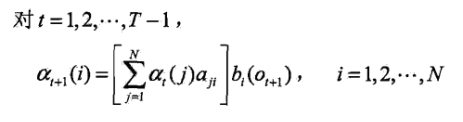
理解一下：
-
(\alpha _{t}(j)*a_{ji}) 时刻 t 观测到o1,o2...ot，并在 t 时刻处于状态 qj ，而在时刻t+1状态为 qi 的联合概率
-
(\sum_{j=1}^{N}\alpha _{t}(j)*a_{ji}) 对所有状态 qj 求和，时刻 t 观测到o1,o2...ot，并在时刻t+1状态为 qi 的联合概率，这一步可以认为是：到t+1状态为qi的前一时刻所有的概率之和。类似下面这个图。
-
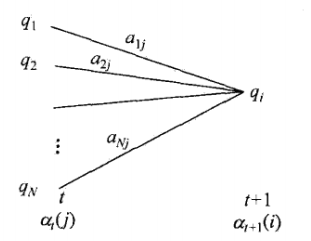
（\sum_{j=1}^{N}\alpha _{t}(j)*a_{ji}*b_{i}(o_{t+1})） 时刻t+1观测到o1,o2...ot+1，且状态为qi ，对比前向概率的定义，可得出此结果即为
终止：
T时刻，所有的状态都加起来（跟状态 i 无关了，也即跟隐藏状态无关了）
2.2后向算法
后向概率：给定hmm，时刻 t，状态为qi 的条件下，从t+1到T的观测为{ot+1,...,oT}的概率
(\beta _{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}|i_{t}=q_{i},\lambda ))
（时刻 t 状态为 i 的情况下，从t+1到T的观测到ot+1....oT的概率，叫后向概率）
初值：
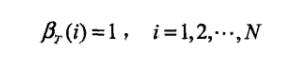
递归：
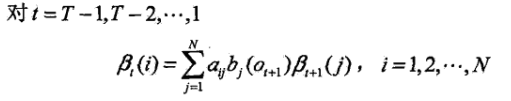
欲求
，可以先看其与
，下一时刻的关系
，时刻t+1状态为 j，从t+2到T的观测为ot+2...oT的概率。
比较一下这两个，就知道，只需要把 t+1 到 t+2 段的概率求出即可，t+2到T是重复的 ，即可用表示
第一种理解：
上一时刻状态 i 转移到下一时刻 j 的概率
上一时刻状态 i ，下一时刻状态 j ，且在状态 j 的条件下，观测为 ot+1的联合概率，注意，这时候要结合，这表示状态 j 观察到ot+2... oT的概率
上一时刻状态 i ，下一时刻状态 j ，且在状态 j 的条件下，观测到ot+1,ot+2...oT的概率
所有状态 j 相加，就跟 j 无关了，类似下面的图
上一时刻状态为 i ，下一时刻观测到ot+1,ot+2...oT的概率
对比一下定义即可得：
\beta _{t}(i)=\sum_{j=1}^{N}a_{ij}*b_{j}(o_{t+1})*\beta _{t+1}(j)
第二种理解：
状态为 j ，观测为ot+2，...，oT的概率
状态为 j ，观测为ot+1，ot+2...oT的概率
上一时刻状态为 i ，下一时刻状态为 j ，且在状态 j 下观测为ot+1，ot+2...oT的联合概率
为什么用 aij ？ 因为要用来表示，时间上来看是后一时刻的状态 j 表示前一时刻的状态 i ，但是前一时刻的状态 i 先发生，后一时刻的状态 j 后发生
这边就一样了，上一时刻状态为 i ，下一时刻观测到ot+1,ot+2...oT的概率
终止：
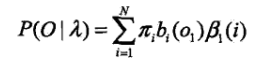
观察一下：
前向计算 T时刻，所有的状态的前向概率都加起来
在模型
下观测序列 {o1,o2...oT} 出现的概率，欲求 ，前向是对
进行求和，可以推测后向应该是搞
时刻 t=1处于状态 i 的条件下，观测为o1的概率
时刻 t=1 状态为 i 观测为 {o2,o3...oT} 的概率
时刻 t=1 状态为 i 观测为 {o1,o2...oT} 的概率
求和，与状态 i 无关，观测为 {o1,o2...oT}的概率
即 
前后向结合起来，可以写成一般形式：
计算概率和期望：
给定模型和观测O，在时刻 t 处于状态 qi 的概率：
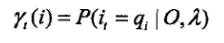
给定模型和观测O，在时刻 t 处于状态 qi ，且在时刻 t+1 处于状态 qj 的概率：
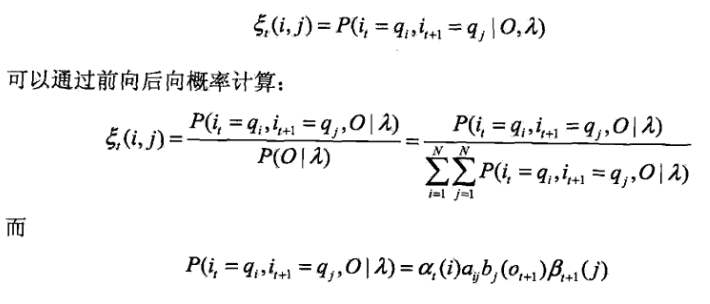
所以
后面部分的参考 隐马尔科夫模型 HMM（一）HMM 模型 ，讲的很细，还有配合的代码
