拉格朗日乘子法

基本的拉格朗日乘子法就是求函数 f(x1,x2,...) 在约束条件 g(x1,x2,...)=0 下的极值的方法。

其主要思想是将约束条件函数与原函数联立，从而求出使原函数取得极值的各个变量的解。

计算过程：

1. 假设需要求极值的目标函数 (objective function) 为 f(x,y)，限制条件为φ(x,y)=M

2. 设

3. 定义一个新函数

4. 用偏导数方法列出方程：

5. 求出 x,y,λ的值，代入即可得到目标函数的极值

如何理解：

代数法：

求一个多元函数 $f(x,y,z,...)$ 在条件 $g(x,y,z,...)=a$ 下的极值, 实际上是求前者在后者定义域下的极值。

而求函数 $L(r,x,y,z,...)=f(x,y,z,...)+r*(g(x,y,z,...)-a)$ 的无条件极值，极值存在的条件为 $L$ 的所有偏导数等于 0。

关键的一点来了，由于 $r$ 也是 $L$ 的变量，所以 $L$ 对 $r$ 的偏导数为 0 相当于要求 $g(x,y,z,...)-a=0$

这恰好使 $L(r,x,y,z,...)$ 的除 $r$ 外的所有变量被限制在 $g(x,y,z,...)$ 的定义域内。

而在这个定义域内，显然 $g-a$ 恒等于 0，于是有 $L=f$ ，求 $f$ 的有条件极值问题被转化为求 $L$ 的无条件极值问题。

几何法1：

这个可以比较直观的解释。

想象一下，目标函数 $f(x,y)$ 是一座山的高度，约束 $g(x,y)=C$ 是镶嵌在山上的一条曲线如下图。

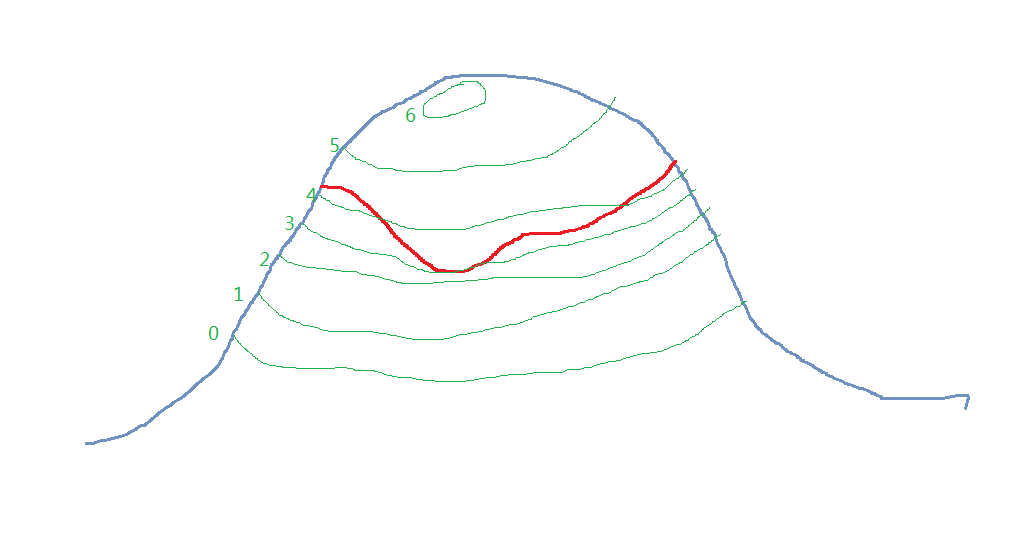
你为了找到曲线上的最低点，就从最低的等高线（0 那条）开始网上数。数到第三条，等高线终于和曲线有交点了（如上图所示）。因为比这条等高线低的地方都不在约束范围内，所以这肯定是这条约束曲线的最低点了。

而且约束曲线在这里不可能和等高线相交，一定是相切。因为如果是相交的话，如下图所示，那么曲线一定会有一部分在 B 区域，但是 B 区域比等高线低，这是不可能的。

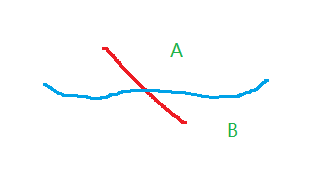
两条曲线相切，意味着他们在这点的法线平行，也就是法向量只差一个任意的常数乘子（取为 $-\lambda$ ）： $\nabla f(x,y)=-\lambda \nabla g(x,y)$ , 我们把这个式子的右边移到左边，并把常数移进微分算子，就得到 $\nabla (f(x,y)+\lambda g(x,y))=0$ 。
把这个式子重新解释一下，这个就是函数 $f(x,y)+\lambda g(x,y)$ 无约束情况下极值点的充分条件。

几何法2：

拉格朗日乘数法（Lagrange multiplier）有很直观的几何意义。
举个 2 维的例子来说明：
假设有自变量 x 和 y，给定约束条件 g(x,y)=c，要求 f(x,y) 在约束 g 下的极值。

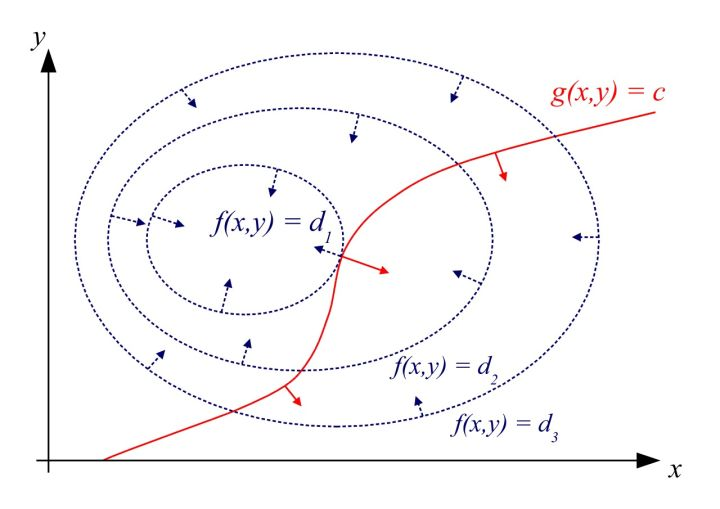
我们可以画出 f 的等高线图，如下图。此时，约束 g=c 由于只有一个自由度，因此也是图中的一条曲线（红色曲线所示）。显然地，当约束曲线 g=c 与某一条等高线 f=d1 相切时，函数 f 取得极值。
两曲线相切等价于两曲线在切点处拥有共线的法向量。因此可得函数 f(x,y) 与 g(x,y) 在切点处的梯度（gradient）成正比。
于是我们便可以列出方程组求解切点的坐标 (x,y)，进而得到函数 f 的极值。