EM算法
含有隐藏变量时,不好直接求极大似然,可以考虑用EM算法。
参考 (EM 算法)The EM Algorithm 从最大似然到 EM 算法浅解
1.Jensen 不等式
回顾优化理论中的一些概念。
设 f 是定义域为实数的函数,如果对于所有的实数 x,
,那么 f 是凸函数。
Jensen 不等式表述如下:
如果 f 是凸函数,X 是随机变量,那么
特别地,如果 f 是严格凸函数,那么![]() 当且仅当
当且仅当![]() ,也就是说 X 是常量。
,也就是说 X 是常量。
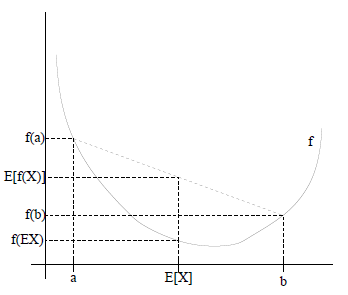
如果用图表示会很清晰:
图中,实线 f 是凸函数,X 是随机变量,有 0.5 的概率是 a,有 0.5 的概率是 b。(就像掷硬币一样)。X 的期望值就是 a 和 b 的中值了,图中可以看到![]() 成立。
成立。
当 f 是(严格)凹函数当且仅当 - f 是(严格)凸函数。
Jensen 不等式应用于凹函数时,不等号方向反向,也就是![]() 。
。
2.EM算法
输入:观测变量数据Y,隐变量数据Z,联合分布 ,条件分布
输出:模型参数
step 1: 选择参数的初值,开始迭代
step 2: 步,记
为第
次迭代参数
的估计值,在第
+1次迭代的
步,计算
函数:
这里 是在给定观测数据Y和当前的参数估计
下隐变量数据Z的条件概率分布
step 3:M步骤,求使得 极大化的
,确定第i+1次迭代的参数的估计值
step 4:重复2,3,直至收敛
思路:
给定的训练样本是![]() ,样例间独立,我们想找到每个样例隐含的类别 z,能使得 p(x,z) 最大。p(x,z) 的最大似然估计如下:
,样例间独立,我们想找到每个样例隐含的类别 z,能使得 p(x,z) 最大。p(x,z) 的最大似然估计如下:
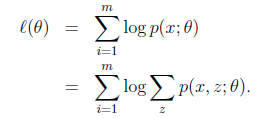
其中分号表示竖线, ,一个意思啊
第一步是对极大似然取对数,第二步是对每个样例的每个可能类别 z 求联合分布概率和。但是直接求![]() 一般比较困难,因为有隐藏变量 z 存在,但是一般确定了 z 后,求解就容易了
一般比较困难,因为有隐藏变量 z 存在,但是一般确定了 z 后,求解就容易了
EM 是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化![]() ,我们可以不断地建立
,我们可以不断地建立![]() 的下界(E 步),然后优化下界(M 步)。这句话比较抽象,看下面的。
的下界(E 步),然后优化下界(M 步)。这句话比较抽象,看下面的。
期望计算方法: 设 Y 是随机变量 X 的函数
(g 是连续函数),那么
(1) X 是离散型随机变量,它的分布律为
,k=1,2,…。若
绝对收敛,则有

证明收敛性





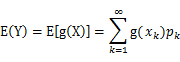

 浙公网安备 33010602011771号
浙公网安备 33010602011771号