最大似然估计
参考 从最大似然到 EM 算法浅解 最大似然估计学习总结 EM 算法及其推广学习笔记
之前已经总结了似然的概念，那么顺其自然的理解就是，求得似然最大值的参数即为想要的参数，也就是参数估计，使用的方法为最大似然估计。
先提出几个问题：
1.最大似然估计求参数的一般流程是怎样的？
2.什么样的场景适合/不适合最大似然估计？为什么
求解步骤：
求导数并令之为 0：
极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。
要求θ，只需要使θ的似然函数 L(θ) 极大化，然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后让导数为 0，那么解这个方程得到的θ就是了（当然，前提是函数 L(θ) 连续可微）。那如果θ是包含多个参数的向量那怎么处理啊？当然是求 L(θ) 对所有参数的偏导数，也就是梯度了，那么 n个未知的参数，就有 n 个方程，方程组的解就是似然函数的极值点了，当然就得到这 n 个参数了。
例子1：
简单1点：1个参数，1个观察值
继续来看例子，假设进行一个实验，实验次数为 10 次，每次实验成功率为 0.2，那么不成功的概率为 0.8，用y 来表示成功的次数。由于前后的实验是相互独立的，所以可以计算得到成功的次数的概率密度为：
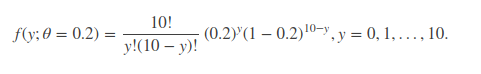
该式子分为两项因子，10 次实验中有y 次成功，那么即在 10 次中随意挑选y 个成功的实验，即C10 y（不好编辑，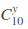
的意思）；第二项为 10 次实验中，y 次实验成功的概率。更一般地，我们可以把每次实验成功的概率当作一个变量θ，则上式可以写为：
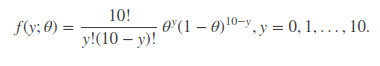
显然，f(y;θ) 是关于随机变量y 和概率参数θ的函数，记作，L(θ)=f(y;θ)。我们这里由于 y 是已知变量，所以似然函数只关于参数θ变化。
好了，现在假设我们在实验室，开始完成某个实验，我们并不知道该实验成功的概率是多少，但做了 10 次实验后，我们只成功了 2 次，用高中的概率知识拿来求解，那不就是实验成功率为 0.2。的确，但由于实验次数相当的小，这里的 0.2 并非是真正的概率，而只是我们实验成功的频率。如抛一枚硬币，抛个 10 次，可能正面朝上的频率为 0.6，但我们都知道，实际正面朝上的概率为 0.5。那如何让频率接近 0.5 呢，不断的增加实验次数即可，你抛个 2 万次试试。所以我们不能简单的就把这个问题中求解的 0.2 作为我们的答案，我们也不可能大量重复实验来统计该实验成功率。遇到这种情况，我们便用到了似然估计方法。
似然函数：
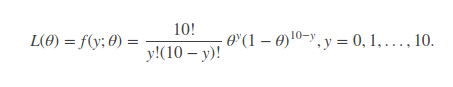
现在我们已知实验次数为 2，我们要求θ使得该似然函数取到极大值， 凭我们主观感受，这个θ应该是0.2。求极值问题只需要对θ求导即可，如果是多参量，那么可以对它求偏导，得到似然方程组，同样能求出想要的解。
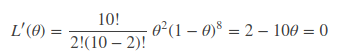
这里没求对数的话，计算很复杂，那求对数呢？会发现计算很方便的。
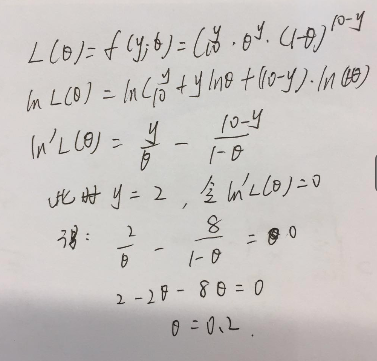
算出来的答案是一样的，这不是多此一举嘛，但上述实验成功次数背后的参数θ模型是一维的，即我们可以用 “肉眼” 来直接看出答案，假如我们这次不是观察实验成功次数，来猜实验成功率，我换个问题问，假设我们班男生身高符合高斯分布，即男生身高概率密度函数符合高斯分布，给你一群男生的身高，请告诉我高斯分布的方差和均值分别是多少？这种情况下，其背后的θ=[μ,π] 含有两个参数，简单的靠肉眼观察显然无法给出答案，因此我们需要借助数学工具，来理论化的证明说，当看到这一群男生的身高时，我们能找到参数θ=[μ,π] 使得出现这群男生身高的概率最大，注意是这群而不是那群！言外之意就是说，θ参数能够对男生进行分类！隐约看出了 EM 算法中的一些思想。
复杂一点：1个参数，多个观察值
我们再把上述问题复杂一下，假设我们现在重复上述实验过程，即第一次，重复实验 10 次，观察到实验成功次数为 1 次；第二次，重复实验 10 次，观察实验成功次数为 2 次。问：你能告诉我实验成功的次数为几次吗？还是用数学严格的进行求解一次！
这里我们有两个观察值，即随机变量y1=1,y2=2，两个随机变量符合相互独立的条件，所以由概率公式得：
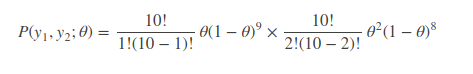
同样的，要求θ使得似然函数取极大值，我们需要对等式进行求导，问题来了，这是 2 个观察值，n 个观察值进行求导，那这复杂得根本无法计算。因此简单的想法就是把求导的乘法法则能够映射到求导的加法法则，因此便有了对数似然函数的引出，即取log 函数，得：
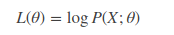
这样对上式进行求导便方便很多，更关键的是，求解出来的θ值与原先的概率分布函数是等价的。
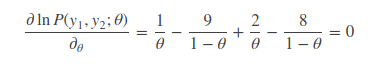
求得θ=0.15。即试验成功的概率为 0.15。
例子2：
多个参数 求偏导
设总体 X~N(μ，σ2)，μ，σ为未知参数，X1,X2...,Xn 是来自总体 X 的样本，X1,X2...,Xn 是对应的样本值，求μ与σ2 的最大似然估计值。
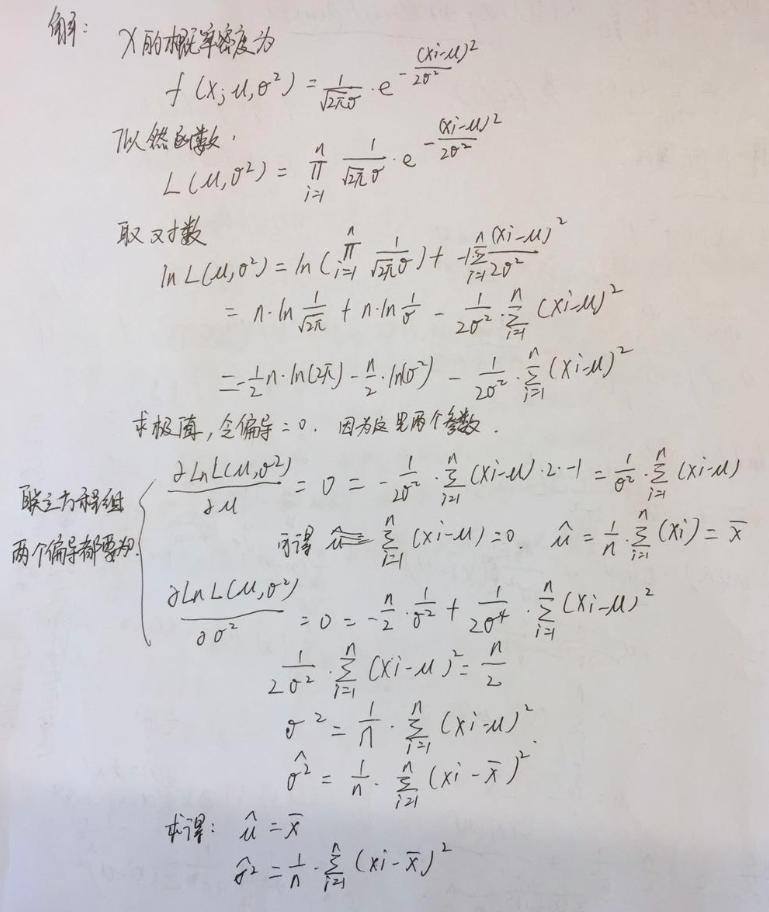
这里要注意，两个偏导为0需同时满足，在各自参数的方向上导数都要为0,才是最终的极值点。
第二个问题：
概率模型中当存在隐变量时，就无法直接用极大似然估计法进行求解
3硬币模型，也是之后引入到EM算法的例子
假设有 3 枚硬币，分别记作 A，B，C。这些硬币正面出现的概率分别是π,p,q. 进行如下投掷试验：先掷硬币 A，根据其结果选出硬币 B 或硬币 C，正面选硬币 B，反而选硬币 C；然后掷选出的硬币，掷硬币的结果，出现正面记作 1，出现反面记作 0；独立地重复 n 次试验（这里，n=10），预测结果如下：
1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果，不能观测掷硬币的过程。也就是只知道最后的结果是正反面，不知道A硬币的结果，也不知道扔的是B还是C硬币，问如何估计三硬币正面出现的概率，即三硬币模型的参数。
同样的，先用先前似然估计方法来求解一波，看看能否给出答案。假设我们知道了一个观测值：
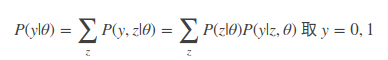
这里y的值取1或0，分别表示正反面。 来直接用θ=(π,p,q) 得
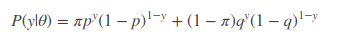
该式子中y 为已知，其他参数均位置，假设我们知道观察序列的第一次投掷结果为 1，因此把y=1 代入得
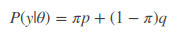
以极大似然方法进行求解，分别对参数π,p,q 进行求导，你会发现对π求导，求出p=q 来，对p,q 分别求导求出π=0 和π=1，显然是没有解析解。因此，传统的似然估计方法是无法解决上述三硬币模型的问题。这也是为什么 EM 算法提出的原因，即它能解决传统求导解决不了的问题。
（遗留一个问题和一个证明，三硬币模型中是由于π的出现，使得似然方程无解？是一旦隐藏变量出现，就无法求解似然方程嘛？如何证明，有谁来证明一下的？不会证明啊）
感觉这道题里面，π就算已知，比如说是0.5,那么可得P(y|θ)=0.5p+0.5q，分别对p，q求导，都是大于0 的啊。感觉无解，那么问题来了，为什么上面的例子2里，求μ，σ2 ，没这个问题，隐藏变量究竟是什么，如何区分和定义。
隐藏变量和参素混淆了，重新理解了一下：
隐藏变量是指无法观测的变量，学生的身高属于正太分布，均值和方差只是参数而已，身高是变量，是可以直接观察的，不属于隐藏变量，而在三硬币模型中，A硬币的状态可以影响到B，C， 但是却无法直接观察到，这才是隐藏变量，至于π,p,q，只是三硬币模型的参数。
