矩阵运算
向量的乘法有两种,分别成为内积和外积.
内积也称数量积,因为其结果为一个数(标量)
向量a,b的内积为|a|*|b|cos,其中表示a与b的夹角
向量外积也叫叉乘,其结果为一个向量,方向是按右手系垂直与a,b所在平面|a|*|b|sin
外积:元素对应乘积 ,Hadamard 乘积 , A的形状m*n, B的形状 n*j, C的形状为 m*j

a1=np.arange(6).reshape(3,2) b1=np.arange(6).reshape(2,3) print a1,'\n',b1 print np.dot(a1,b1)
[[0 1] [2 3] [4 5]] a1
[[0 1 2] [3 4 5]] b1
[[ 3 4 5] [ 9 14 19] [15 24 33]]
性质:
服从分配率

服从结合率

乘积转置
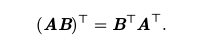
python中矩阵的一些操作:
#!/usr/bin/python #coding=utf-8 #__author__='dahu' #官网https://docs.scipy.org/doc/numpy-dev/reference/arrays.classes.html#matrix-objects import numpy as np a=np.mat('1 2 3; 4 5 3') #以分号结尾的生成形式 print a #常见矩阵 print np.mat(np.zeros((3,4))),'全0' print np.mat(np.ones((3,4))),'全1' print np.mat(np.eye(3,4)),'单位矩阵' #单位矩阵,注意单位矩阵的输入格式跟上面两个不一样 print np.mat(np.diag(range(5))),'对角矩阵' print np.mat(np.random.rand(2,3)),'创建2行3列的矩阵,每个元素的大小在0,1之间' print np.mat(np.random.randint(1,5,size=(3,4))),'创建3行4列矩阵,每个元素范围在[1,5)' #矩阵运算 a1=np.arange(6).reshape(3,2) a1=np.mat(a1) #注意mat也是工厂函数,继承于ndarray b1=np.mat(np.arange(6).reshape(2,3)) print a1,'a1\n',b1.T,'b1转置' print np.multiply(a1,b1.T),'俩矩阵对应元素相乘,俩矩阵列的个数要相等' print a1*2 ,'矩阵乘标量,点乘' print np.dot(a1,b1) ,'矩阵叉乘,前一个的列和后一个的行相等' #矩阵操作 print a1.T ,'转置' print a1.H ,'共轭转置' print a1.I ,'逆矩阵' print np.dot(a1.I,a1),'矩阵的逆叉乘矩阵,为单位矩阵' print a1.A,type(a1.A),'去除矩阵格式,返回数组' #计算矩阵对应行列的最大、最小值、和 print a1.sum(),'全部求和' print a1.sum(axis=0),'列和,2列求和,行就抵消了,返回1行2列的矩阵' print a1.sum(axis=1),'行和,3行求和,返回3行1列的矩阵' print a1.max(),'数值,a1矩阵中所有元素的最大值' print np.max(a1,0),'a1矩阵中各列的最大值组成一个1行多列的矩阵' print np.max(a1,1),'行的最大值' print np.argmax(a1,0),'列的最大值在该列中的索引' #矩阵的分隔和合并 c=np.mat(np.ones((3,3))) print c[1:,1:],'分割,第二行和第二列以后所有的元素' d1=np.mat(np.ones((2,2))) d2=np.mat(np.eye(2)) print np.vstack((d1,d2)),'按列合并,增加行数' print np.hstack((d1,d2)),'按hang合并,增加列数' #矩阵,数组,列表互相转换 >>>a1=[[1,2],[3,2],[5,2]] #列表 >>> a1 [[1, 2], [3, 2], [5, 2]] >>>a2=array(a1) #将列表转换成二维数组 >>> a2 array([[1, 2], [3, 2], [5, 2]]) >>>a3=mat(a1) #将列表转化成矩阵 >>> a3 matrix([[1, 2], [3, 2], [5, 2]]) >>>a4=array(a3) #将矩阵转换成数组 >>> a4 array([[1, 2], [3, 2], [5, 2]]) >>>a41=a3.getA() #将矩阵转换成数组 >>>a41 array([[1,2] [3,2] [5,2]]) >>>a5=a3.tolist() #将矩阵转换成列表 >>> a5 [[1, 2], [3, 2], [5, 2]] >>>a6=a2.tolist() #将数组转换成列表 >>> a6 [[1, 2], [3, 2], [5, 2]]
/usr/bin/python2.7 /home/dahu/Homework/GMM的EM算法实现/矩阵练习.py [[1 2 3] [4 5 3]] [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] 全0 [[ 1. 1. 1. 1.] [ 1. 1. 1. 1.] [ 1. 1. 1. 1.]] 全1 [[ 1. 0. 0. 0.] [ 0. 1. 0. 0.] [ 0. 0. 1. 0.]] 单位矩阵 [[0 0 0 0 0] [0 1 0 0 0] [0 0 2 0 0] [0 0 0 3 0] [0 0 0 0 4]] 对角矩阵 [[ 0.49413545 0.30732574 0.99311351] [ 0.18276303 0.84983583 0.00383651]] 创建2行3列的矩阵,每个元素的大小在0,1之间 [[3 3 1 3] [1 3 4 2] [1 2 3 2]] 创建3行4列矩阵,每个元素范围在[1,5) [[0 1] [2 3] [4 5]] a1 [[0 3] [1 4] [2 5]] b1转置 [[ 0 3] [ 2 12] [ 8 25]] 俩矩阵对应元素相乘,俩矩阵列的个数要相等 [[ 0 2] [ 4 6] [ 8 10]] 矩阵乘标量,点乘 [[ 3 4 5] [ 9 14 19] [15 24 33]] 矩阵叉乘,前一个的列和后一个的行相等 [[0 2 4] [1 3 5]] 转置 [[0 2 4] [1 3 5]] 共轭转置 [[-1.08333333 -0.33333333 0.41666667] [ 0.83333333 0.33333333 -0.16666667]] 逆矩阵 [[ 1.00000000e+00 9.43689571e-16] [ -3.33066907e-16 1.00000000e+00]] 矩阵的逆叉乘矩阵,为单位矩阵 [[0 1] [2 3] [4 5]] <type 'numpy.ndarray'> 去除矩阵格式,返回数组 15 全部求和 [[6 9]] 列和,2列求和,行就抵消了,返回1行2列的矩阵 [[1] [5] [9]] 行和,3行求和,返回3行1列的矩阵 5 数值,a1矩阵中所有元素的最大值 [[4 5]] a1矩阵中各列的最大值组成一个1行多列的矩阵 [[1] [3] [5]] 行的最大值 [[2 2]] 列的最大值在该列中的索引 [[ 1. 1.] [ 1. 1.]] 分割,第二行和第二列以后所有的元素 [[ 1. 1.] [ 1. 1.] [ 1. 0.] [ 0. 1.]] 按列合并,增加行数 [[ 1. 1. 1. 0.] [ 1. 1. 0. 1.]] 按hang合并,增加列数 Process finished with exit code 0




 浙公网安备 33010602011771号
浙公网安备 33010602011771号