FSMN 及其变种 cFSMN DFSMN pyramidal-FSMN
原文: https://blog.csdn.net/qq_26778411/article/details/89682447
也可以参考: http://vsooda.github.io/2018/03/12/fsmn/
1.FSMN 综述
由于 Bi-RNN 较高的成功率需要得到整段语音所有未来信息的支持才能实现,因此会带来较长的硬延时,故 Bi-RNN 不适合作为在线语音识别的模型。故在 2015 年科大讯飞提出了 FSMN(Feedforward Sequential Memory Networks)模型,该模型在很小的延时下,就能取得与 Bi-RNN 一样的效果。
详见论文:
(1)Feedforward Sequential Memory Neural Networks without Recurrent Feedback 该篇篇幅较短,只介绍了 FSMN 在 Language Model 的应用。
(2)Feedforward Sequential Memory Networks: A New Structure to Learn Long-term Dependency 该篇较为详细的描述了 FSMN 的三个变种,在 Acoustic Model 和 Language Model 上的应用。
在 FSMN 的基础之上,陆陆续续又出现了 cFSMN、DFSMN、pyramidal-FSMN 等 FSMN 的变种。
(1)cFSMN:Compact Feedforward Sequential Memory Networks for Large Vocabulary Continuous Speech Recognition
(2)DFSMN:Deep-FSMN for Large Vocabulary Continuous Speech Recognition
(3)pyramidal-FSMN:A novel pyramidal-FSMN architecture with lattice-free MMI for speech recognition
2.FSMN
前面提到了,有两篇论文讲述了 FSMN,这里就选取较为全面的第二篇 Feedforward Sequential Memory Networks: A New Structure to Learn Long-term Dependency 进行讲解。
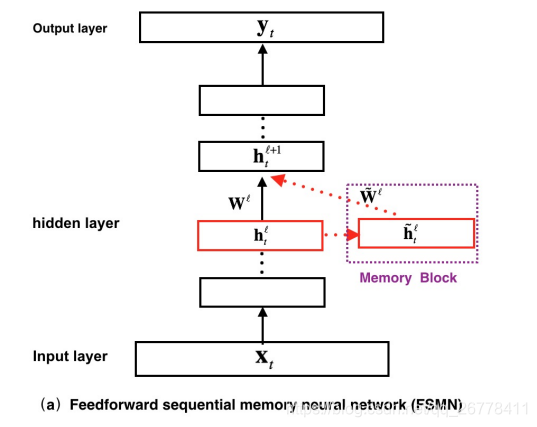
FSMN 的结构如上图所示,在图中我们可以看到,FSMN 对比普通的前馈神经网络,最大的区别就是引入了 Memory Block. 该 Memory 的表达式如下:
h˜ℓt=∑Ni=0aℓi⋅hℓt−ih~tℓ=∑i=0Naiℓ⋅ht−iℓ \tilde{\mathbf{h}}_{t}^{\ell}=\sum_{i=0}^{N} a_{i}^{\ell} \cdot \mathbf{h}_{t-i}^{\ell}
h~tℓ=i=0∑Naiℓ⋅ht−iℓ
其中,hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell}
ht−iℓ为t−it−i t-i
t−i 时刻ℓℓ \ell
ℓ层的 features,aℓiaiℓ a_{i}^{\ell}
aiℓ为对应的时不变系数。
这里可以看出,Memory Block 中储存了NN N N 个hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell} ht−iℓ的 “过去记忆”,该 “过去记忆h˜ℓth~tℓ \tilde{\mathbf{h}}_{t}^{\ell} h~tℓ” 会与当前层的 features hℓthtℓ \mathbf{h}_{t}^{\ell} htℓ一起前向传入下一层。
当然,不难想到,该 Memory Block 也可以通过引入部分延时来存储 “未来的记忆”,改进后的表达式如下:
h˜ℓt=∑N1i=0aℓi⋅hℓt−i+∑N2j=1cℓj⋅hℓt+jh~tℓ=∑i=0N1aiℓ⋅ht−iℓ+∑j=1N2cjℓ⋅ht+jℓ \tilde{\mathbf{h}}_{t}^{\ell}=\sum_{i=0}^{N_{1}} a_{i}^{\ell} \cdot \mathbf{h}_{t-i}^{\ell}+\sum_{j=1}^{N_{2}} c_{j}^{\ell} \cdot \mathbf{h}_{t+j}^{\ell}
h~tℓ=i=0∑N1aiℓ⋅ht−iℓ+j=1∑N2cjℓ⋅ht+jℓ
其中,hℓt+jht+jℓ \mathbf{h}_{t+j}^{\ell}
ht+jℓ为t+jt+j t+j
t+j 时刻ℓℓ \ell
ℓ层的 features,cℓiciℓ c_{i}^{\ell}
ciℓ为对应的时不变系数。
文章中对 Memory Block 中时不变系数aℓiaiℓ a_{i}^{\ell}
aiℓ和hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell}
ht−iℓ的运算 (⋅⋅ \cdot
⋅) 进行了分类:
(1) 若aℓiaiℓ a_{i}^{\ell}
aiℓ为一个常数,则该 FSMN 被称为 sFSMN,aℓiaiℓ a_{i}^{\ell}
aiℓ和hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell}
ht−iℓ之间的运算为标量相乘。
(2) 若aℓiaiℓ a_{i}^{\ell}
aiℓ是一个与hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell}
ht−iℓ等长的向量,则该 FSMN 被称为 vFSMN, aℓiaiℓ a_{i}^{\ell}
aiℓ和hℓt−iht−iℓ \mathbf{h}_{t-i}^{\ell}
ht−iℓ之间的运算为 dot product.
文章解释了 FSMN 的 Memory Block 可以替代 RNN 中原因:
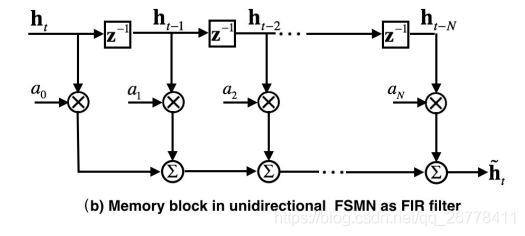
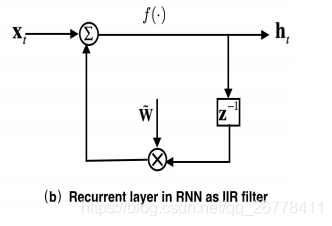
如上图所示,RNN 中的循环结构可以看成一个 IIR 滤波器 (z−1z−1 z^{-1} z−1 为上一时刻导数的 Z 变换),FSMN 中的 Memory 可以看成一个 FIR 滤波器。根据信号与系统的知识我们知道,IIR 滤波器可以通过高阶的 FIR 滤波器逼近表示。所以 FSMN 中的 Memory Block 可以看成是 RNN 中循环结构的近似。由于 FSMN 在同一层中的某时刻的输入不需要依赖上一时刻的输出,所以网络的训练时间对比 RNN 会大大缩短。
FSMN 的参数更新公式为:
h˜ℓt=∑N1i=0aℓi⊙hℓt−i+∑N2j=1cℓj⊙hℓt+jh~tℓ=∑i=0N1aiℓ⊙ht−iℓ+∑j=1N2cjℓ⊙ht+jℓ \tilde{\mathbf{h}}_{t}^{\ell}=\sum_{i=0}^{N_{1}} \mathbf{a}_{i}^{\ell} \odot \mathbf{h}_{t-i}^{\ell}+\sum_{j=1}^{N_{2}} \mathbf{c}_{j}^{\ell} \odot \mathbf{h}_{t+j}^{\ell}
h~tℓ=i=0∑N1aiℓ⊙ht−iℓ+j=1∑N2cjℓ⊙ht+jℓ
hℓ+1t=f(Wℓhℓt+W˜ℓh˜ℓt+bℓ)htℓ+1=f(Wℓhtℓ+W~ℓh~tℓ+bℓ) \mathbf{h}_{t}^{\ell+1}=f\left(\mathbf{W}^{\ell} \mathbf{h}_{t}^{\ell}+\tilde{\mathbf{W}}^{\ell} \tilde{\mathbf{h}}_{t}^{\ell}+\mathbf{b}^{\ell}\right) htℓ+1=f(Wℓhtℓ+W~ℓh~tℓ+bℓ)
3.cFSMN
如果使用 FSMN,设该层和下一层的神经元的个数均为nn n n 时,"前向记忆" 的个数为N1N1 N_1 N1,"后向记忆" 的个数为N2N2 N_2 N2,该层的参数个数为:n∗n+n∗n+n∗(N1+N2)n∗n+n∗n+n∗(N1+N2) n*n+n*n+n*(N_1+N_2) n∗n+n∗n+n∗(N1+N2) 个。当nn n n 很大,训练参数就会很多。
为了解决 FSMN 参数较多的问题,文章 Compact Feedforward Sequential Memory Networks for Large Vocabulary Continuous Speech Recognition 提出了 cFSMN,该文章借鉴了矩阵低秩分解的思路在网络中引入了一个维数较小的 project 层,通过该 project 层进行降维,从而实现减少训练参数个数的目的。
cFSMN 的结构如下图所示:
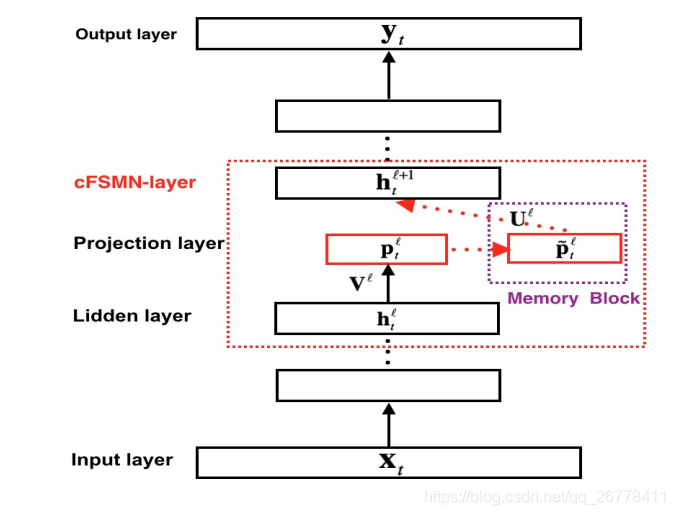
cFSMN 的参数更新公式为:
pℓt=Vℓhℓtptℓ=Vℓhtℓ \mathbf{p}_t^{\ell}=\mathbf{V}^{\ell}\mathbf{h}_t^{\ell}
ptℓ=Vℓhtℓ
p˜ℓt=pℓt+∑N1i=0aℓi⊙pℓt−i+∑N2j=1cℓj⊙pℓt+jp~tℓ=ptℓ+∑i=0N1aiℓ⊙pt−iℓ+∑j=1N2cjℓ⊙pt+jℓ \tilde{\mathbf{p}}_{t}^{\ell}=\mathbf{p}_{t}^{\ell}+\sum_{i=0}^{N_{1}} \mathbf{a}_{i}^{\ell} \odot \mathbf{p}_{t-i}^{\ell}+\sum_{j=1}^{N_{2}} \mathbf{c}_{j}^{\ell} \odot \mathbf{p}_{t+j}^{\ell}
p~tℓ=ptℓ+i=0∑N1aiℓ⊙pt−iℓ+j=1∑N2cjℓ⊙pt+jℓ
hℓ+1t=f(Uℓp˜ℓt+bℓ+1)htℓ+1=f(Uℓp~tℓ+bℓ+1) \mathbf{h}_{t}^{\ell+1}=f\left(\mathbf{U}^{\ell} \tilde{\mathbf{p}}_{t}^{\ell}+\mathbf{b}^{\ell+1}\right)
htℓ+1=f(Uℓp~tℓ+bℓ+1)
设 project 层的 features 个数为pp p p, 该层和下一层的神经元的个数均为nn n n, 则 cFSMN 参数的个数为n∗p+p∗(N1+N2)+n∗pn∗p+p∗(N1+N2)+n∗p n*p+p*(N_1+N_2)+n*p n∗p+p∗(N1+N2)+n∗p.
4.DFSMN
因为每个 cFSMN 层中包含了较多的子层,一个包含 4 个 cFSMN 层,2 个 DNN 层的 cFSMN 网络总共需要 12 层结构。若通过直接增加 cFSMN 层的方法来设计更深的 cFSMN 网络,网络可能会出现梯度消失的问题。
针对上述问题,文章 Deep-FSMN for Large Vocabulary Continuous Speech Recognition 提出了 DFSMN,该 DFSMN 在 cFSMN 的 Memory Block 之间添加了 skip connection,使低层的 memory 可以直接流入高层的 Memory Block 中。在反向传播的过程当中,高层的梯度也会直接流入低层的 Memory Block 中,这样有助于克服梯度消失的情况。DFSMN 的结构如下图所示:
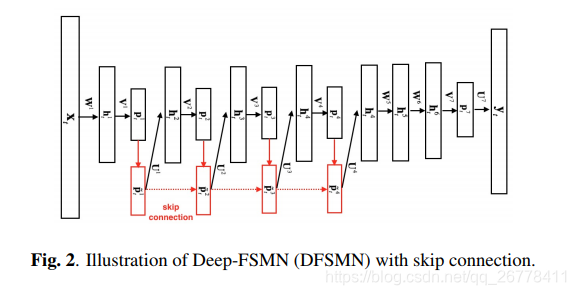
DFSMN 的参数更新公式为:
pℓt=Vℓhℓtptℓ=Vℓhtℓ \mathbf{p}_t^{\ell}=\mathbf{V}^{\ell}\mathbf{h}_t^{\ell}
ptℓ=Vℓhtℓ
p˜ℓt=ℋ(p˜ℓ−1t)+pℓt+∑Nℓ1i=0aℓi⊙pℓt−s1∗i+∑Nℓ2j=1cℓj⊙pℓt+s2∗jp~tℓ=H(p~tℓ−1)+ptℓ+∑i=0N1ℓaiℓ⊙pt−s1∗iℓ+∑j=1N2ℓcjℓ⊙pt+s2∗jℓ \tilde{\mathbf{p}}_{t}^{\ell}=\mathcal{H}\left(\tilde{\mathbf{p}}_{t}^{\ell-1}\right)+\mathbf{p}_{t}^{\ell}+\sum_{i=0}^{N_{1}^{\ell}} \mathbf{a}_{i}^{\ell} \odot \mathbf{p}_{t-s_{1} * i}^{\ell}+\sum_{j=1}^{N_{2}^{\ell}} \mathbf{c}_{j}^{\ell} \odot \mathbf{p}_{t+s_{2} * j}^{\ell}
p~tℓ=H(p~tℓ−1)+ptℓ+i=0∑N1ℓaiℓ⊙pt−s1∗iℓ+j=1∑N2ℓcjℓ⊙pt+s2∗jℓ
hℓ+1t=f(Uℓp˜ℓt+bℓ+1)htℓ+1=f(Uℓp~tℓ+bℓ+1) \mathbf{h}_{t}^{\ell+1}=f\left(\mathbf{U}^{\ell}\tilde{\mathbf{p}}_{t}^{\ell}+\mathbf{b}^{\ell+1}\right)
htℓ+1=f(Uℓp~tℓ+bℓ+1)
ℋ(p˜ℓ−1t)H(p~tℓ−1) \mathcal{H}\left(\tilde{\mathbf{p}}_{t}^{\ell-1}\right) H(p~tℓ−1) 表示低层 Memory Block 与高层 Memory Block 的连接形式。若将低层的 Memory 直接添加到高层的 Memory Block 中,则ℋ(p˜ℓ−1t)=p˜ℓ−1tH(p~tℓ−1)=p~tℓ−1 \mathcal{H}\left(\tilde{\mathbf{p}}_{t}^{\ell-1}\right)=\tilde{\mathbf{p}}_{t}^{\ell-1} H(p~tℓ−1)=p~tℓ−1。
5.pyramidal-FSMN
pyramidal-FSMN 是云从科技 2018 年刷新 Librispeech 数据集正确率最高记录时使用的模型中的一部分。详情见论文 A novel pyramidal-FSMN architecture with lattice-free MMI for speech recognition。
文章认为在 DFSMN 的结构中,若直接将底层的 Memory Block 的 Memory 直接添加到上层的 Memory Block 中,这将导致上层和底层拥有相同记忆,这么做是非常冗余的。文章提出的 pyramidal-FSMN 结构,它相比于 DFSMN 有两点不一样:第一点改变是底层的 Memory Block 较小,越高层的 Memory Block 依次变大,文章认为这样的结构可以用底层提取音素信息,而用高层提取到语义和语法特征;第二点改变是在 skip connection 连接底层和上层的 Memory Block 时,只有在 Memory Block 的 size 不一样时,才进行连接。
pyramidal-FSMN 中 Memory Block 的更新公式为:
xlt=xl−mt+∑Nl1i=0ali⊙hlt−s1∗i+∑Nl2j=0bli⊙hlt+s2∗jxtl=xtl−m+∑i=0N1lail⊙ht−s1∗il+∑j=0N2lbil⊙ht+s2∗jl x_{t}^{l}=x_{t}^{l-m}+\sum_{i=0}^{N_{1}^{l}} a_{i}^{l} \odot h_{t-s_1 * i}^{l}+\sum_{j=0}^{N_{2}^{l}} b_{i}^{l} \odot h_{t+s_2 * j}^{l}
xtl=xtl−m+i=0∑N1lail⊙ht−s1∗il+j=0∑N2lbil⊙ht+s2∗jl




 浙公网安备 33010602011771号
浙公网安备 33010602011771号