红黑树原理、查找效率、插入及变化规则分析
引言
在文章《各种查找算法的选用分析(顺序查找、二分查找、二叉平衡树、B树、红黑树、B+树)》中我们分析过,红黑树的本质其实就是对概念模型:阶数为4的B树——“2-3-4树”的一种实现,也能从文章中看出选用红黑树的优点。
下面我们分析一下为什么红黑树的本质其实就是对概念模型:阶数为4的B树——“2-3-4树”的一种实现。
和2-3-4树的关系
2-3-4树就是阶数为4的B树。红黑树是对概念模型2-3-4树的一种实现,由于直接进行不同节点间的转化会造成较大的开销,所以选择以二叉树为基础,在二叉树的属性中加入一个颜色属性来表示2-3-4树中不同的节点。2-3-4树到红黑树的转化过程:
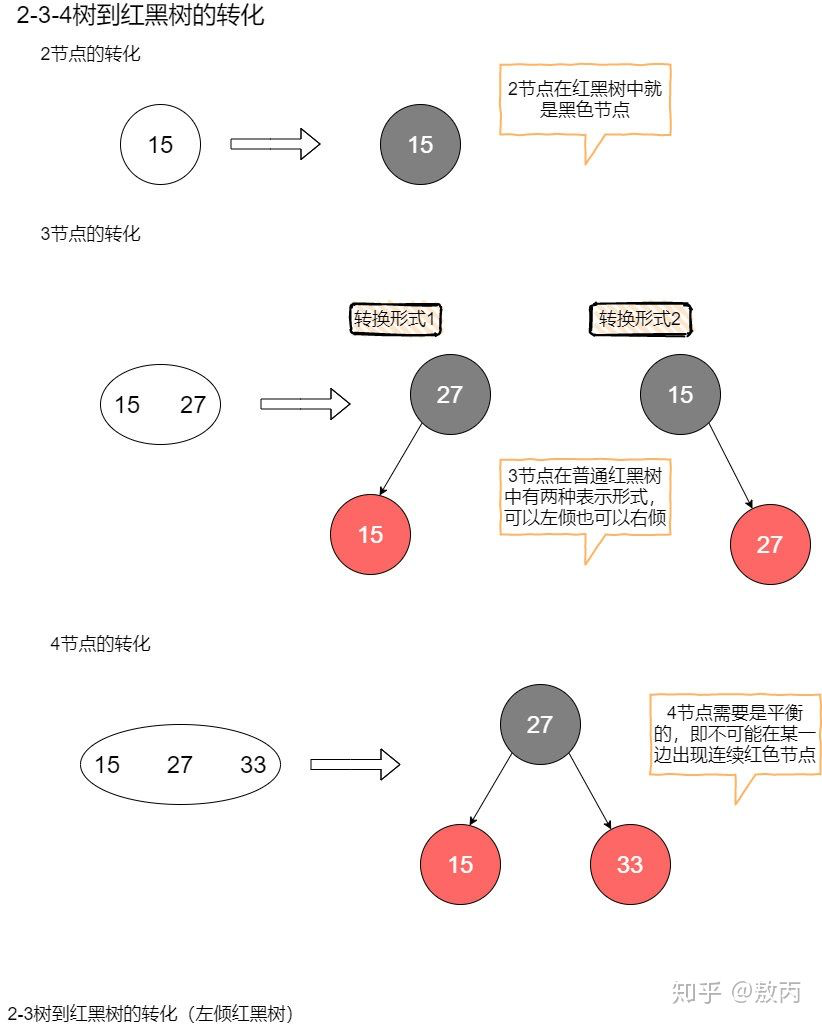
举个例子,对比一下插入过程就更加能体会2-3-4树和红黑树的关系了。分别向红黑树、2-3-4树依次插入2、3、4、5、6、7:
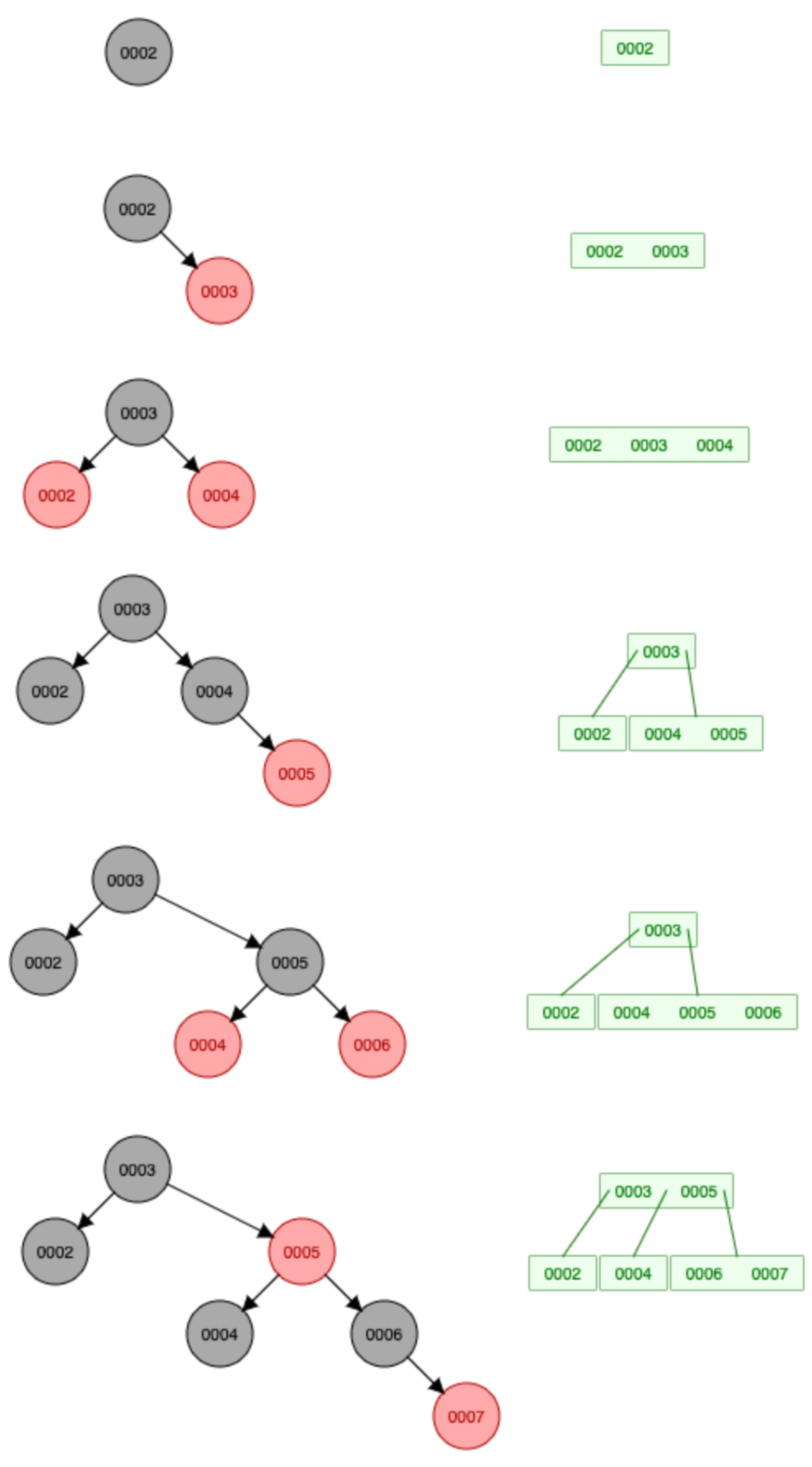
红黑树
定义
红黑树需要满足如下四个要求:
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点,也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
通过对2-3-4树和红黑树关系的讲解,其实就可以体会到,红黑树定义中的这四个要求,其实就是为了让红黑树始终是变形的2-3-4树。
- 黑色节点对应的就是每个2-3-4树节点中间的那个键值
- 三个键值的中间:(0+2)/2=1
- 两个键值的中间:(0+1)/2=0
- 红色节点对应的就是每个2-3-4树节点两边的那个键值
所以不可能有两个连续的红色节点、根节点必须是黑色、每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点。
再体会下红黑树和2-3-4树的对应关系:
Case 含义 父子都是黑色节点 代表的是2-3-4树中,上一层节点的中间键值指向下一层的中间键值 父是黑色节点,子是红色 代表的是2-3-4树中,同一个节点中的中间键值指向两边键值 父是红色节点,子是黑色 代表的是2-3-4树中,上层节点中的两边键值指向下一层的中间键值
红黑树的查找效率
通过分析红黑树和2-3-4树的关系,其实大概就能体会到红黑树的查找效率应该是和B树差不多的(毕竟B树中,找到一个节点后,往下应该顺着哪个分支找,也是要通过计算的)。
接下来我们再具体地分析一下红黑树的查找效率。如果把红黑树中的所有红色节点拿掉,然后拿这些节点的爷爷节点作为父节点,你会发现,它变成了一个4阶平衡树。
原因是这条定义:
每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
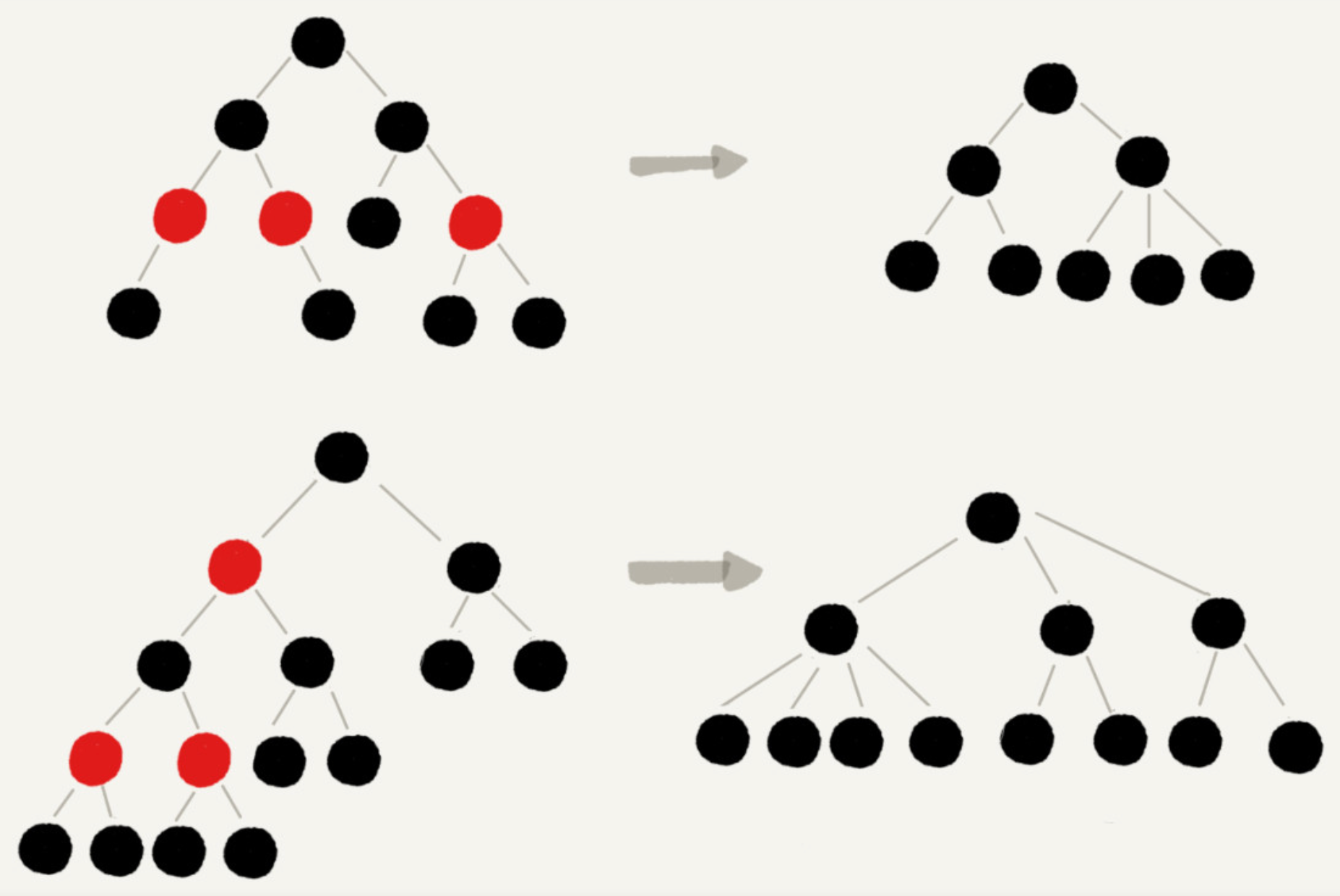
所以变换后的树的查找的效率为 。我们现在知道只包含黑色节点的“黑树”的高度,那我们现在把红色节点加回去,高度会变成多少呢?
。我们现在知道只包含黑色节点的“黑树”的高度,那我们现在把红色节点加回去,高度会变成多少呢?
因为任何相邻的节点都不能同时为红色,所以红色节点不能相邻,也就是说,有一个红色节点就要至少有一个黑色节点,将它跟其他红色节点隔开。所以加入红色节点后,即使树高变成了两倍,那么查找的效率也不会高于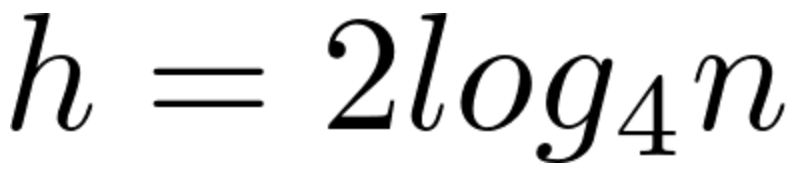 。
。
红黑树的插入及变化规则
插入及变化规则
在极客时间中老师用了魔方的例子来讲解其思想,我觉得很恰当.这里直接拿来用
不知道你有没有玩过魔方?其实魔方的复原解法是有固定算法的:遇到哪几面是什么样子,对应就怎么转几下。你只要跟着这个复原步骤,就肯定能将魔方复原。
实际上,红黑树的平衡过程跟魔方复原非常神似,大致过程就是:遇到什么样的节点排布,我们就对应怎么去调整。只要按照这些固定的调整规则来操作,就能将一个非平衡的红黑树调整成平衡的。
新插入的节点必须为红色。
所以如果父节点是黑色的话,插入后还是满足红黑树定义,
不需要调整。如果没有父节点,或者父节点为红色,则分为以下四种需要调整的情况:
| 情况 | 调整方式 | 调整步骤 | 举例 |
|---|---|---|---|
| 1.没有父节点(当前节点为红黑树的根节点) | 变色 | 将该红色节点变成黑色 | |
| 当前节点的父亲是红色,且它的叔叔节点也是红色 | 变色 | 1. 把父节点、叔叔节点设为黑色 2. 把爷爷节点设为红色 |
例子1 |
| 1. 当前父节点是红色,叔叔节点是黑色 2. 当前的节点是右子树 |
左旋 | 以父节点作为根节点左旋 | 例子2 |
| 1. 当前父节点是红色,叔叔节点是黑色 2. 当前的节点是左子树 |
右旋 | 以父节点作为根节点右旋 | 例子3 |
如果每次调整后,如果调整后的树不符合红黑树定义,则继续根据上述4种情况调整,直至成为合格的红黑树。
例子1
情况:
- 当前节点的父亲是红色,且它的叔叔节点也是红色
调整:变色
- 把父节点、叔叔节点设为黑色
- 把爷爷节点设为红色
例子2
情况:
- 当前父节点是红色,叔叔节点是黑色
- 当前的节点是右子树
调整:左旋
- 以父节点作为根节点左旋
例子3
情况:
- 当前父节点是红色,叔叔节点是黑色
- 当前的节点是左子树
调整:左旋
- 以父节点作为根节点右旋
红黑树的插入及变化规则,对应在2-3-4树中是什么操作?
1. 新插入的节点必须为红色
其实向B树中插入节点时,也是这样的过程,先把键值放到对应的节点上,然后看节点的键值是否超过最大的键值数
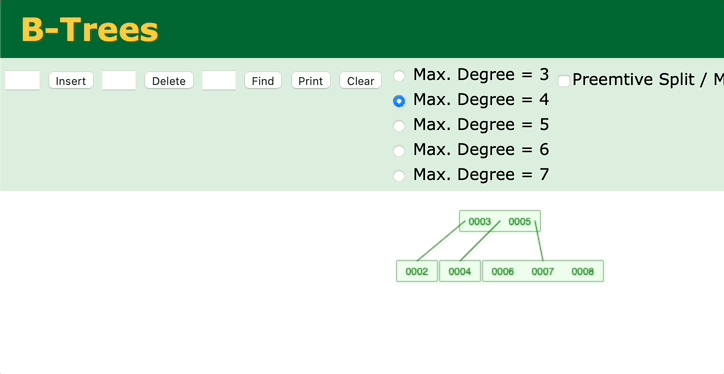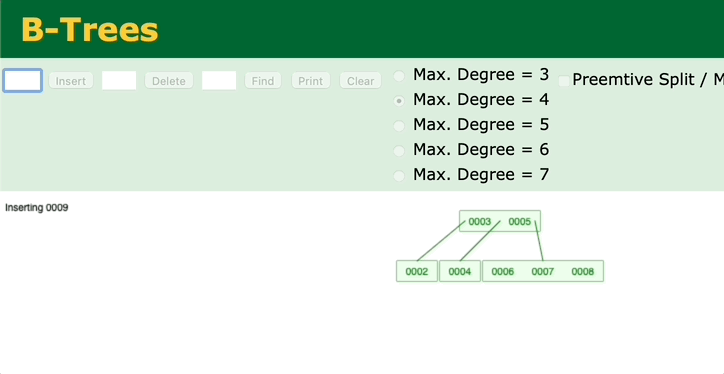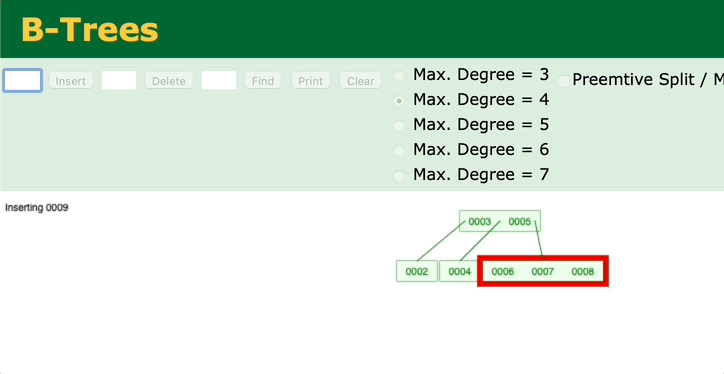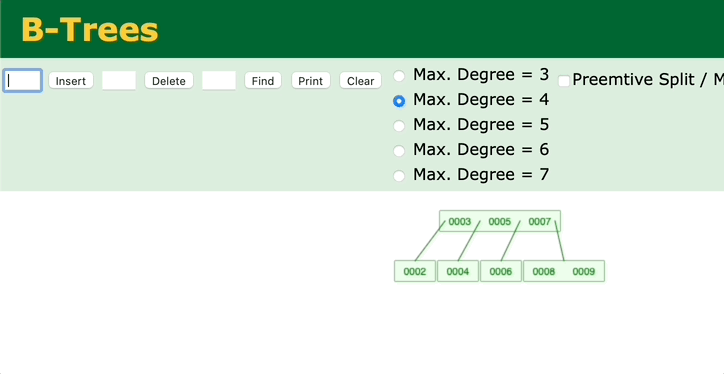
2. 没有父节点(当前节点为红黑树的根节点)
略
3. 当前节点的父亲是红色,且它的叔叔节点也是红色
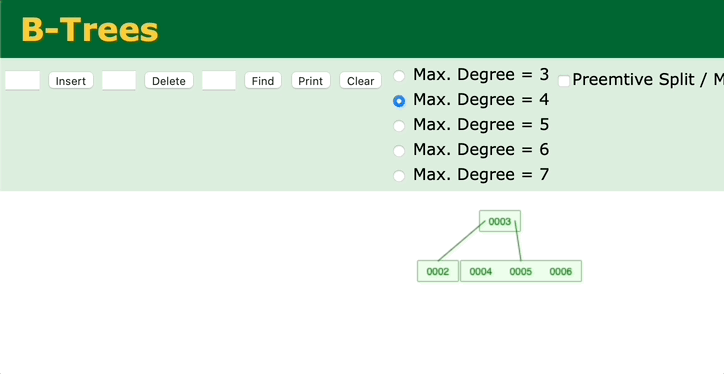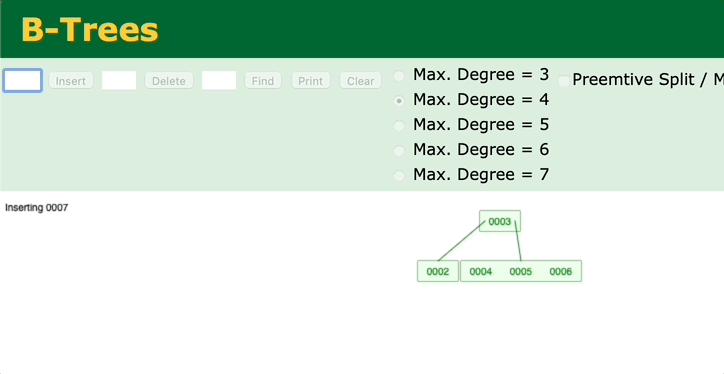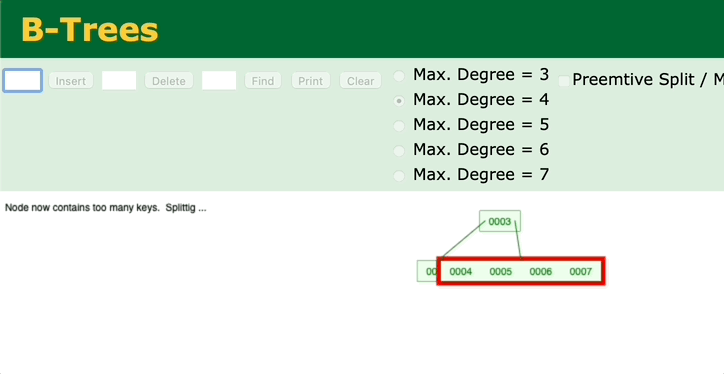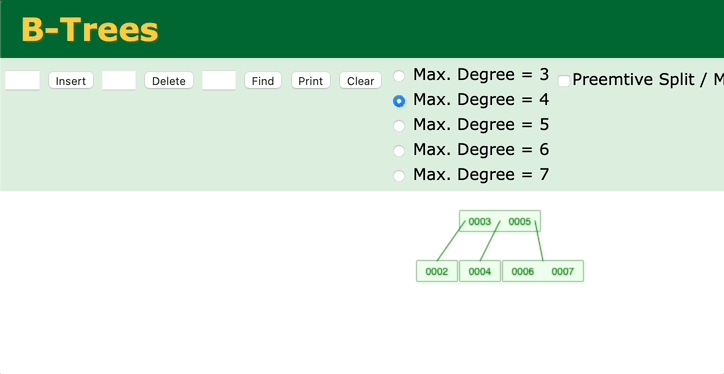
是不是对应了变色的过程?
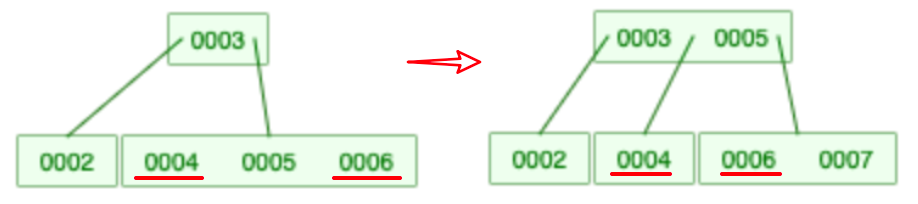
4. 当前父节点是红色,叔叔节点是黑色;当前的节点是右子树
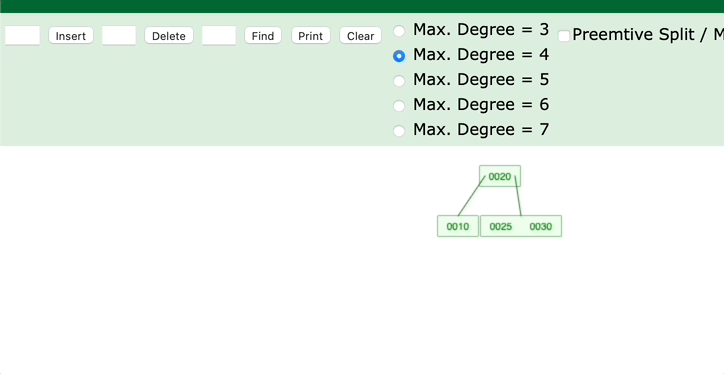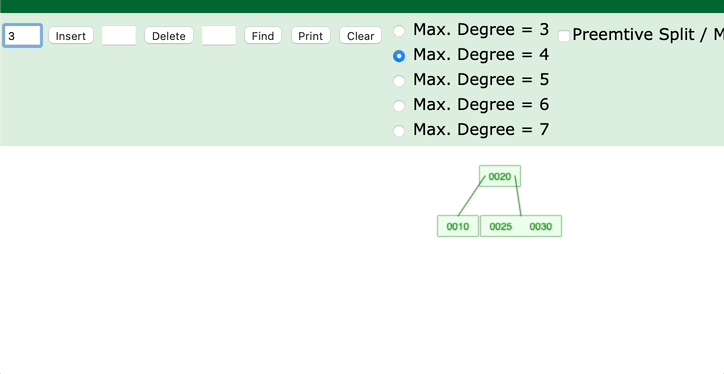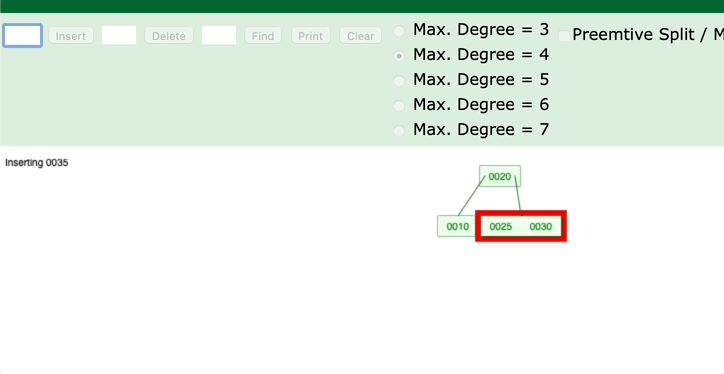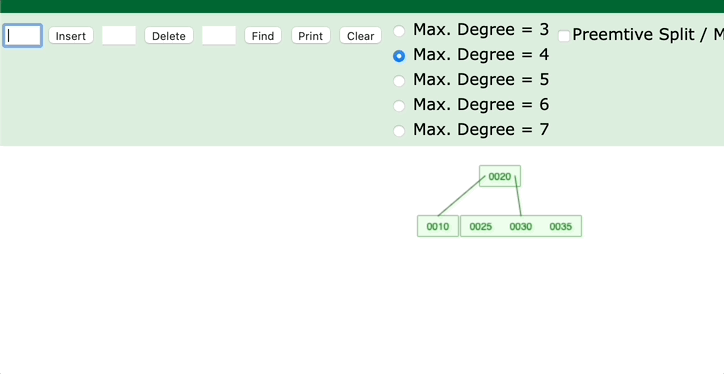
是不是对应了左旋的过程?
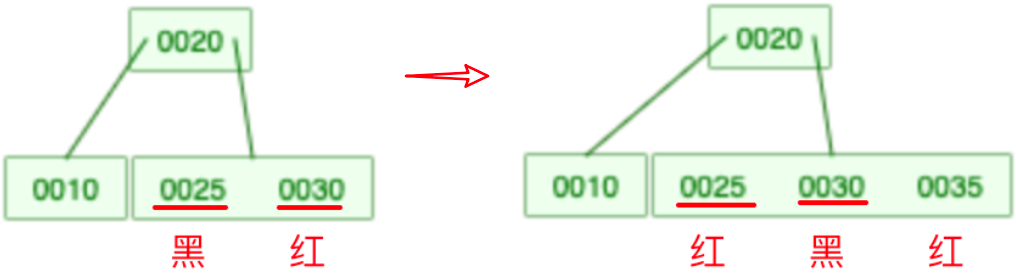
5. 当前父节点是红色,叔叔节点是黑色;当前的节点是左子树
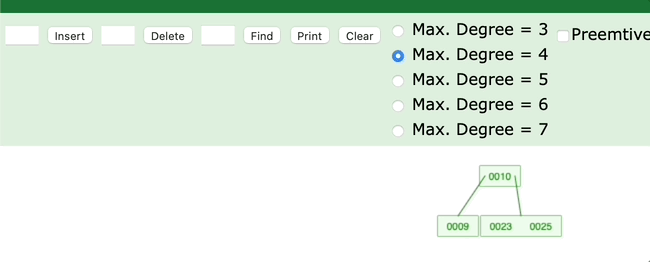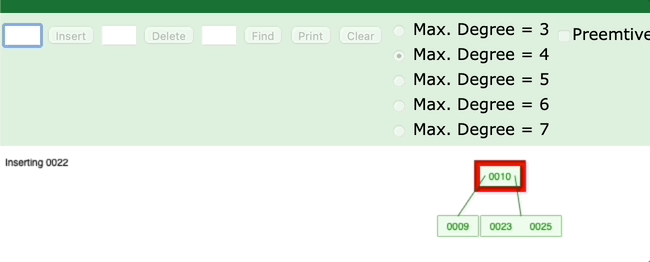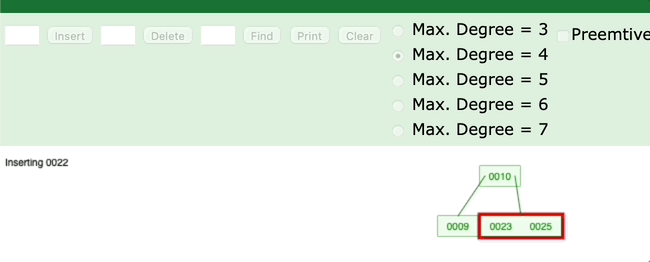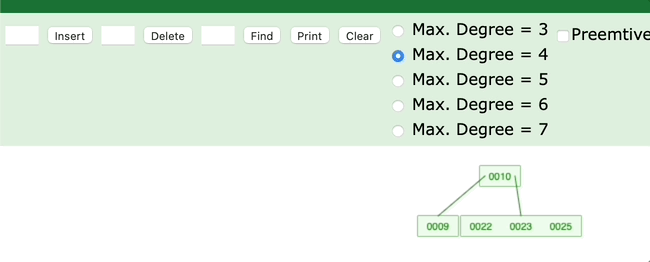
是不是对应了右旋的过程?



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义