机器学习中的方差和偏差
对一个学习算法除了通过实验估计其泛化性能,还需要更好的了解泛化能力的原因,偏差-方差分解时解释算法泛化性能的一种重要的工具。
对于测试样本x,令yD为x在数据集中的标记(可能存在噪声导致标记值和真实值不同),y为x的真实值,f(x;D)在训练集D上学得模型f在x上的输出。以回归任务为例:
学习算法的期望预测为:
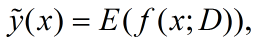
就是所有预测值的平均值;
产生的方差的计算为:

方差就是表示在某测试数据集上的方差,都是测试数据集上的预测值之间的关系,与真实的值并没有关系
对于噪声定义为:

标记值与真实值差平方的期望。
偏差则定义成期望输出与真实标记的差别:
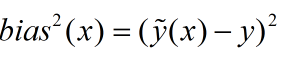
为了便于讨论,假设噪声的期望为0.通过简单的多项式展开与合并对算法的期望泛化误差进行分解:
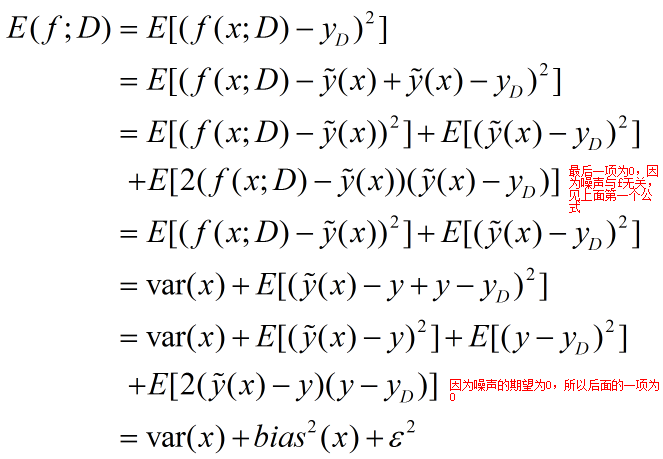
偏差度量了学习算法的期望预测与真实结果的偏离程度,刻画描述了算法本身对数据的拟合能力,也就是训练数据的样本与训练出来的模型的匹配程度;方差度量了训练集的变化导致学习性能的变化,描述了数据扰动造成的影响;噪声则表示任何学习算法在泛化能力的下界,描述了学习问题本身的难度。偏差方差分解表示了泛化性能有三者决定。
一般来说偏差和方差有冲突称之为偏差-方差窘境。在给定学习任务下,在训练不足时,学习器的拟合能力较弱,,训练数据的扰动不足以使学习器产生明显变化,此时偏差起到最要的作用,随着学习器拟合能力的加强,偏差越来越小,但是任何一点数据抖动都可以被学习,方差逐渐占据主导,若训练数据自身的非全局的特性被学习到了,那么久发生了过拟合。




