汉诺塔(Hanoi)问题分析与递归求解—C/C++
/*传闻在越南的首都河内有一座古塔,名曰汉诺塔,塔内有三根柱子,第一根柱子上有从下向上从大到小的64个盘子。一天,众僧朝拜,佛曰:“若按照一次只能移动一个盘子到柱子上并且大盘子不能压在小盘子上的规则,把这64个盘子从第一根柱子移动到第三根柱子上,那么大同世界就要到来了...”*/
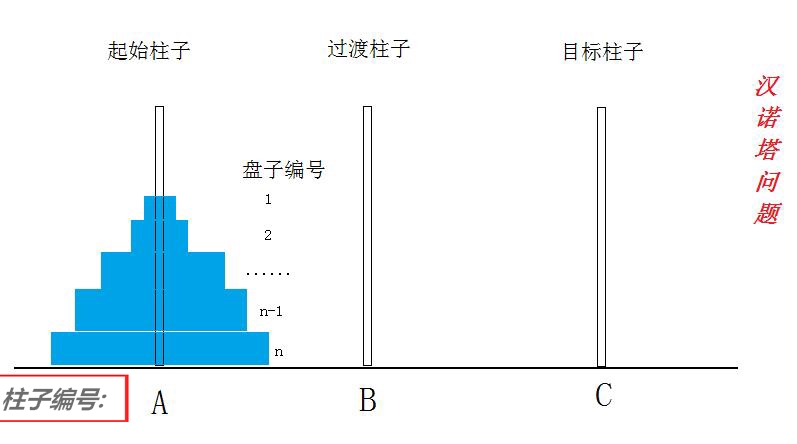
算法思想:把n个盘子从起始柱子A移动到目标柱子C的过程可以分解为:①先把前n-1个盘子从起始柱子A移动到过渡柱子B(此时C作为跳板),
②再把编号为n的盘子直接从起始柱子A移动到目标柱子C,③最后把这n-1个盘子从过渡柱子B移动到目标柱子C(此时A作为跳板).
下面给出代码 和 移动步数step关于盘子个数n的函数及其数学归纳法证明.
#include<stdio.h>
#include<windows.h>
int step = 0; //记录移动操作的总步数
//将编号为n的盘子从start柱子移动到end柱子
void Move(int n,char start,char end)
{
printf("~~~ 将编号为 %d 的盘子从 %c 柱子移动到 %c 柱子 ~~~\n",n,start,end);
step++;
}
//汉诺塔递归函数
//把transition作为中间过渡的柱子,将total个盘子从start柱子移动到destination柱子
void Handle(int total,char start,char transition,char destination)
{
if(total==1) //递归边界
Move(total,start,destination);
else{
Handle(total-1,start,destination,transition); //先把前n-1个盘子移动到transition过渡柱子(此时把destination柱子作为过渡柱子)
Move(total,start,destination); //然后把最后最大的盘子移动到destination柱子
Handle(total-1,transition,start,destination); //最后把n-1个盘子从transition柱子移动到destination柱子(此时把start柱子作为过渡柱子)
}
}
int main()
{
int n;
printf("请输入起始柱子的数目: ");
scanf("%d",&n);
printf("\n");
Handle(n,'A','B','C');
printf("\n总共需要 %d步 移动操作~\n\n",step);
system("pause");
return 0;
}
/* 由程序运行结果得出:
n = 1时,步数为 1;
n = 2时,步数为 3;
n = 3时,步数为 7;
n = 4时,步数为 15;
n = 5时,步数为 31;
......
通过前几个结果不难递推得出步数为:2的n次方-1
下面我们通过数学归纳法来严格证明这一结论
证明:
n = 1时, 步数 [S1] = 1;
则当n = 2时,步数 [S2] = [S1] + 1 + [S1]; //Note:
n = 3时, 步数 [S3] = [S2] + 1 + [S2]; //移动k个盘子的步数为先移动前k-1个盘子到过渡柱子的步数([Sk-1]) 加上
...... // 第k个盘子直接移动到目标柱子的步数(为1) 加上
n = k时, 步数 [Sk] = [Sk-1] + 1 + [Sk-1]; // 这k-1个盘子从过渡柱子移动到目标柱子的步数 (这一步操作等效于刚开始的前k-1个盘子移动到过渡柱子的步数[Sk-1])
当n = k+1时,步数 [Sk+1] = [Sk] + 1 + [Sk];
即: [Sk+1] + 1 = 2[Sk] +2 = 2( [Sk] + 1) //左右两边同时+1
( [Sk+1] + 1) ÷ ( [Sk] + 1) = 2; //等比
设 [Bn] = [Sn] + 1,n >= 1,则[Bn]为等比数列,公比q = 2,
由等比数列公式得:
[Bn] = [B1] * q(n-1次方) = ( [S1] + 1) * q(的n-1次方) = (1 + 1)*2(n-1次方) = 2(的n次方),其中n >= 1;
所以 [Sn] = [Bn] - 1 = 2(的n次方) - 1,其中 n >= 1;
证毕.
*/
由此看出,若按照一秒搬一个盘子的速度,则需要2的64次方-1秒才能搬完64个盘子,2的64次方-1秒 = 18446744073709551615秒 = 584942417654.6年
大同世界就要到来了-.- 倒计时中: 584942417654.6年.....





