Python基础【第五周】:自定义函数、PyInstaller库、递归讲解
函数的定义:



函数可以有参数,也可以没,必须保留括号。
函数定义时可以为某些参数指定默认值,构成可选参数。

非可选参数也称为默认参数,即函数内部有初始值
1 def handle(x,type='mysql'): 2 print(x,type) 3 4 handle('hello') 5 handle('hello',type='sqlite') 6 handle('hello','sqlite') 7 #就相当于如果不传这个参数,就会有个默认值,因为函数里面会用到这个参数
输出:
1 hello mysql 2 hello sqlite 3 hello sqlite
多参数传递:

1 #demo1.py 2 def test(a,*b): 3 print(a,b) 4 5 test(1,3,4,5)#可变参数以逗号为元素分隔形成一个元祖 6 test(1,*(3,4,5))#完整写法,与上述结果一样 7 test(1,"kobe","bryant") 8 test(1,("james","kobe"))#元祖("james","kobe")单独形成一个元素
输出:
1 1 (3, 4, 5) 2 1 (3, 4, 5) 3 1 ('kobe', 'bryant') 4 1 (('james', 'kobe', 'allen'),)

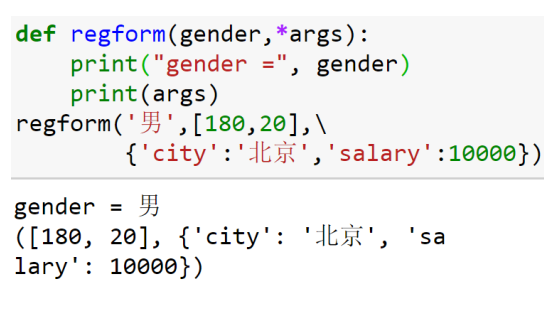
关于返回值:函数可以有一个,多个,或者没有返回值(多个返回值形成元祖输出)
1 def test(a,b): 2 return a,a +b,a*b 3 4 print(test(2,3))#输出(2,5,6)
局部变量和全局变量

规则1:局部变量和全局变量是不同的变量
局部变量是函数内定义的变量,函数结束,空间就被释放了;可以在函数内部使用global保留字使用全局变量。
1 #demo1.py 2 a ,s = 3,10 3 print(id(s))#输出全局变量s的存储地址8791214576960 4 def test(a): 5 s = 0 6 print(id(s))#输出局部变量的存储地址8791214576640 7 for i in range(1,a+1): 8 s += i 9 return s#此时局部变量s的值为6 10 print (test(a),s)#全局变量依旧是s = 10
使用global定义全局变量:
1 #demo1.py 2 a ,s = 3,0 3 print(id(s))#输出全局变量s的存储地址8791208940864 4 def test(a): 5 global s 6 print(id(s))#输出局部变量的存储地址8791208940864 7 for i in range(1,a+1): 8 s += i 9 return s#此时s的值为6 10 print(test(a),s)#输出6 6 :证明s的值已经被改变,储存地址也说明了
规则2:局部变量为组合数据类型且未创建,等同于全局变量
1 #demo1.py 2 list1 = ["kobe","jordan"] 3 print(id(list1)) 4 def test(a): 5 list1.append(a) 6 print(id(list1)) 7 test("james") 8 print(list1) 9 '''输出: 10 3891784 11 3891784 12 ['kobe', 'jordan', 'james'] 13 因为在方法中list1并未创建,故会在全局搜寻变量list1'''
错误示范:
1 #demo1.py 2 list1 = ["kobe","jordan"] 3 print(id(list1)) 4 def test(a): 5 list1 = [] 6 list1.append(a) 7 print(id(list1)) 8 test("james") 9 print(list1) 10 '''输出: 11 5399112 12 5399176 13 ['kobe', 'jordan'],因为在方法中重新定义了一个局部变量空列表list1,所以两者不一样'''
lambda函数:是一种匿名函数,没有名字;使用lambda保留字定义,函数名是返回结果;可以写在一行内。

表达式就是返回值。
示例:
1 #demo1.py 2 fn = lambda a,b:a+b 3 print(fn(2,3)) 4 f = lambda : "I love Kobe"#a+b和I love Kobe均是表达式,相当于return返回 5 print(f()) 6 #输出: 7 '''5 I love Kobe'''

函数递归:减少代码量的重要思维
递归的定义:


递归就是数学归纳法思维的编程体现。
递归本来是一个函数,需要函数定义方式描述;
函数内部,采用分支语句对输入参数进行判断;
基例和链条,分别编写对应代码———上述例子中基例就是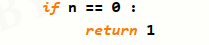
链条就是
当计算n=5时,计算机此时状态。
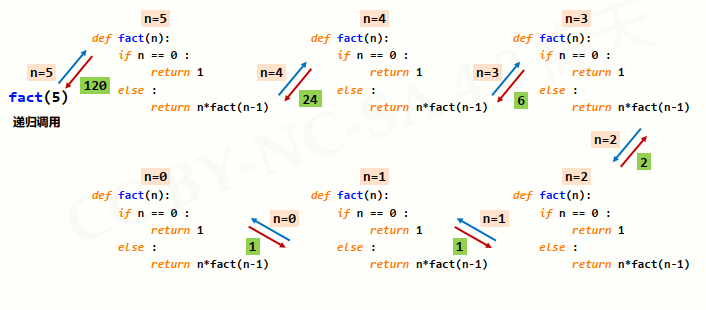
先蓝再红
计算fact(5),执行链条,计算机开辟新的空间计算fact(4),继续执行链条,计算机又开辟新的空间,计算fact(3),,,,,,知道计算fact(0)计算机得到值fact(0) = 1,所以fact(1)得到答案,,,,,,从而fact(5)得到答案。
递归的过程,就是计算机运算过程,将函数定义理解为一个模板,计算在对每一个赋予的参数去运算的时候,会将函数的模板拷贝一份,放到计算机的某一个位置,然后用实际给定的参数去运算,如果实际给定的参数还要用此函数运算,那么计算机又开辟一个新的内存,拷贝一段一样的代码,直到计算至基例。
实例讲解1:字符串反转。(若不用递归,可以使用s[::-1])
思想:1.函数 + 分支结构的组合:分清哪些是基例,哪些是链条;
2.(字符串最小形式是什么?)显然是空字符串,所以基例选择空字符串;
3.原始字符串将第一个放到最后一个,再将第二个放到最后一个,,,,,,
代码:
1 def rev(s):
2 if s == "":
3 return s
4 else:
5 return s[-1]+rev(s[0:-1])
6 print(rev("kobe bryant"))
嵩天老师版本:

斐波那锲数列也是递归的经典。此处不赘述。
实例讲解2:汉诺塔问题
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。

假设只有两个圆盘,一大一小,所以先将左边小圆盘放到中间,再将大圆盘放到右边,再将中间的小圆盘放到最右边。
思想:1.需要输出两个参数,一个是需要的步骤数count,一个是该怎么搬运:抽象为a,b,c三根柱子,写出步骤a->b······.
2.四个输入参数,一个是圆盘数量n,第二个参数是源柱子src,第三个是目的柱子dst,第四个是过度柱子mid。
3.试想一下,如果只有两个圆盘,该怎么搬运呢。当然是将a第一个圆盘放到b,再将第二个圆盘放到c,再将b的圆盘放到c。那么如果有n个圆盘,那么可以将n看成第n个和前n-1个的整体两部分,所以想到可以先将前面第n-1个圆盘搬到过渡柱子b,再将a剩下的一个最大的圆盘搬到c,这时候不就变成了b有n-1个圆盘(将b看为起始柱子),c有一个最大的盘(c依旧为目标柱子),a是空柱子(看作过渡);然后再将n-1个圆盘看做两部分(第n-1个和前n-2个),再进行上述步骤········直到全部转移至c柱子

程序:
1 #demo2.py 2 count = 1 3 def hanoi(n,src,trans,dst):#src为起始柱子,trans为过渡,dst为目标柱子 4 global count 5 if n == 1: 6 print("第{}步:{}->{}".format(count,src,dst)) 7 count += 1 8 else : 9 hanoi(n-1,src,dst,trans)#将n-1看做整体先移动到过渡柱子 10 print("第{}步:{}->{}".format(count,src,dst)) 11 count += 1 12 hanoi(n-1,trans,src,dst)#将原来的过渡柱子和起始柱子交换位置 13 hanoi(3,"A","B","C")
1 第1步:A->C 2 第2步:A->B 3 第3步:C->B 4 第4步:A->C 5 第5步:B->A 6 第6步:B->C 7 第7步:A->C
PyInstaller库的使用
作用:将我们编写的扩展名为.py的python源代码转化成无需源代码的可执行文件。因为可能在windows,linux等各种平台并没有安装python的IDLE或者解释器,故不可以通过源代码执行,所以需要将源程序编译打包成一个直接可以执行的程序。PyInstaller就可以实现这一功能。
如PyInstaller可以将.py的文件转化为.exe的形式,从而可以在windows平台下执行。
第三方库的安装
安装第三方库需要使用pip工具,不可以在IDLE环境下去安装它,因为它是需要安装运行的第三方库。
我们需要用windows下的command命令行或者linux平台等相应命令行。
在命令行直接使用:pip install PyInstaller
注意:有时候下载速度会非常慢,然后出现红色字体错位,一般是镜像问题,可以使用以下命令行:
pip install packagename -i http://pypi.douban.com/simple --trusted-host pypi.douban.com
国内其他镜像有:
清华:https://pypi.tuna.tsinghua.edu.cn/simple
阿里云:http://mirrors.aliyun.com/pypi/simple/
中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/
华中理工大学:http://pypi.hustunique.com/
山东理工大学:http://pypi.sdutlinux.org/
豆瓣:http://pypi.douban.com/simple/
本人使用的是豆瓣,亲测有效,十秒之内安装好PyInstaller。
上述是临时使用,也可一劳永逸,改变镜像:
windows下,直接在user目录中创建一个pip目录,再新建文件pip.ini。(例如:C:\Users\WQP\pip\pip.ini)内容为:
[global] index-url = https://pypi.tuna.tsinghua.edu.cn/simple [install] trusted-host=mirrors.aliyun.com
PyInstaller的使用
使用windows命令行操作,不要使用IDLE命令行,因为PyInstaller是命令行的执行程序,不是Python下的执行程序
使用 : pyinstaller -F <文件名.py>(注:文件名要写绝对目录,或者直接在命令行中进入文件所在目录)
举例:使用七段数码管绘制当前时间的程序。
部分执行情况:
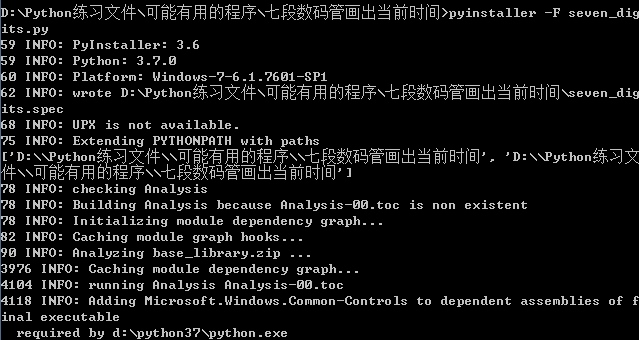
我们可以看到原来的文件夹中生出了额外的三个目录:
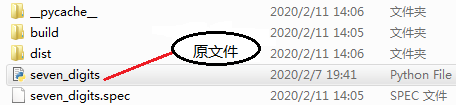
其中的build和_pycache_文件夹可以放心删除掉,而在dist目录中你可以看到与原文件同名的.exe文件。
双击即可执行。
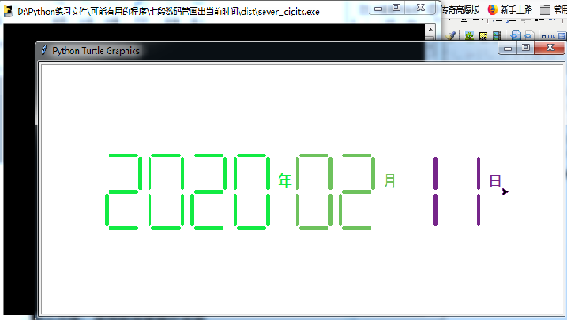
我们还可以改变PyInstaller的参数
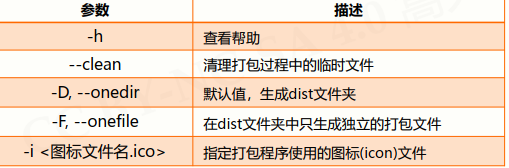
最常用的是 -h 可以显示此工具可以完成的功能
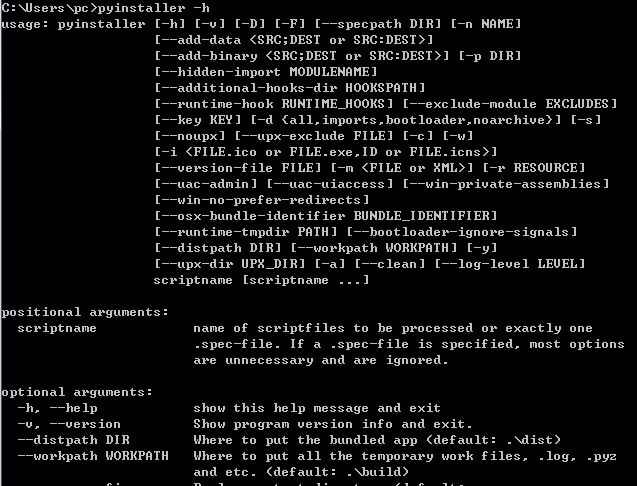
--clean 就是删除临时文件,比如上述的build、_pycache_文件夹。
-i <图标文件名.ico> : 指定打包程序使用的图标(icon)文件
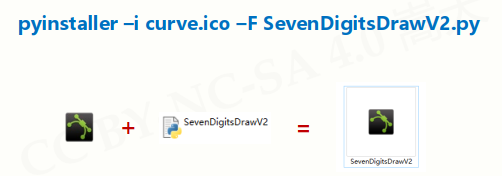
打包完成的程序可以直接发送,对方只要是windows平台就可以执行,无需安装任何东西






