Python第二周:初始turtle库画图
案例展示
结果展示

程序展示
1 #PythonDraw.py 2 import turtle 3 turtle.setup(650, 350, 200, 200) 4 turtle.penup() 5 turtle.fd(-250) 6 turtle.pendown() 7 turtle.pensize(25) 8 turtle.pencolor("purple") 9 turtle.seth(-40) 10 for i in range(4): 11 turtle.circle(40, 80) 12 turtle.circle(-40, 80) 13 turtle.circle(40, 80/2) 14 turtle.fd(40) 15 turtle.circle(16, 180) 16 turtle.fd(40 * 2/3) 17 turtle.done()
程序解析
- #PythonDraw.py
这是文件名,写Python文件时开头注释文件名
- import turtle
导入turtle作图的库
- for循环
range(4)会生成一个序列,并不是列表,其使用一般是用于for循环及生成有规律的数组,可利用list()转化为列表。参考https://www.runoob.com/python/python-func-range.html
turtle的初识
原理:有一只海龟,其实在窗体正中心,在画布上游走,走过的轨迹形成了绘制的图形
, 海龟由程序控制,可以变换颜色、改变宽度等
。
turtle最小单位是像素。
turtle的绘图窗体:

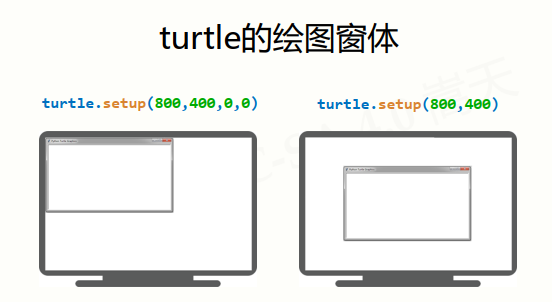


方法turtle.goto(x,y)是由当前位置向坐标(x,y)移动,并留下直线轨迹。

turtle.circle(r,angle)是以r为半径,在当前方向基础上旋转angle角度;turtle(r):默认旋转360

turtle.setheading(angle) ,别名turtle.seth(angle)
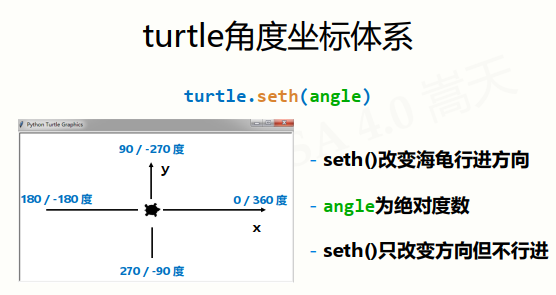
seth()方法是在0度基础上改变
而left(angle),right(angle)方法是在原有基础上改变
turtle.bk(d),turtle.fd(d)分别是后退和前进d距离,原名是turtle.back(d) ,turtle.forward(d)
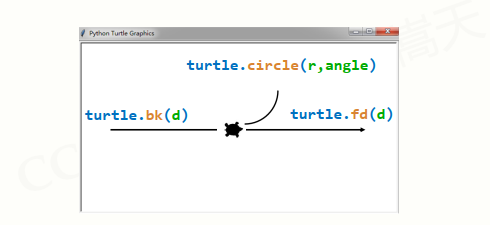
关于turtle的一些方法
turtle.penup()和turtle.pendown()是一对。其中penup()是提笔,从此移动不形成轨迹,用于另起一个地方绘制;pendown()则是关闭。


关于RGB:

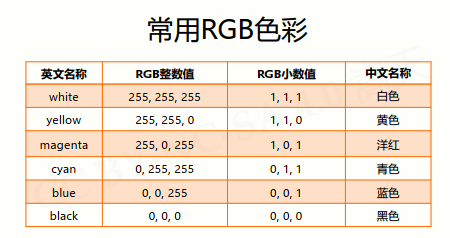
具体的颜色的对应可见取色板
turtle.pensize(25):改变画笔的粗细
更多方法可见链接:https://blog.csdn.net/Xin_101/article/details/85850265
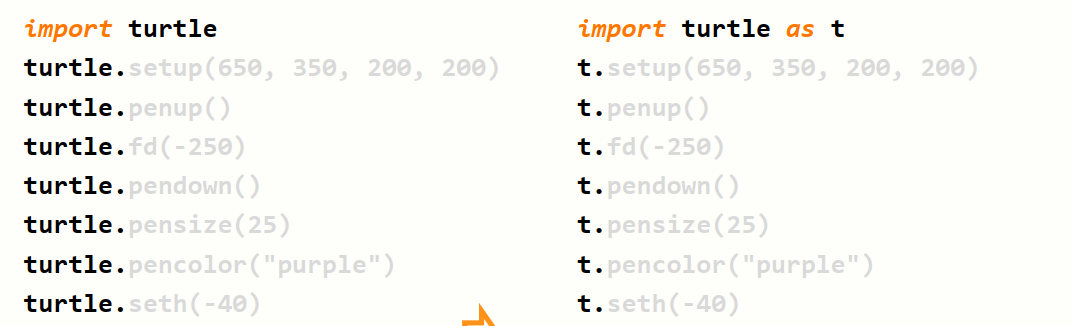
编码风格
第一种:a.b(参数)
a为库名,b为方法名。缺点:较为繁琐。
例:turtle.circle(100,180)
第二种:b(),b为方法名字
使用前提:在引入库的时候使用:from a import b或者from a import *
缺点:可能方法名与编程者所使用的方法名冲突;优点:方便

第三种:自定义名字
使用方法:import a as b
a是原始库名,b为自定义库名
实例2:七段数码管绘制(来自于第五周学习)


代码:解释均在注释处

1 #stopwatch.py 2 #目的:输入需要倒计时的秒数,利用turtle库进行计时 3 #方法drawconstant(numbers,gap)目的在于画出连续的一串数字 4 #number是一串连续数字,gap为数字之间的间隔,默认为5 5 #number_list是元素为单个数字的列表 6 #方法list(map(int,list(number_str)))是将list中每一个元素转化为数字形成的map对象再转化为list 7 def drawconstant(numbers,gap=15): 8 number_str = str(numbers) 9 number_list = list(map(int,list(number_str))) 10 for s in number_list: 11 drawdigit(s) 12 turtle.penup() 13 turtle.fd(gap) 14 #stopwatch(numbers)在于输入秒数numbers进行倒计时 15 #sleep(1)为程序停止一秒 16 #turtle.reset()是清空画布,回归原始 17 def stopwatch(numbers): 18 for i in range(numbers,-1,-1): 19 turtle.pensize(5) 20 turtle.pencolor(random.random(), random.random(), random.random()) 21 drawconstant(i, gap=15) 22 time.sleep(1) 23 turtle.reset() 24 #drawdigit(numbers)是画出单个数字,一个数字分七步走 25 def drawdigit(number): 26 # 第一步: 27 drawline(True) if number in [2, 3, 4, 5, 6, 8, 9] else drawline(False) 28 # 第二步 29 drawline(True) if number in [0, 3, 4, 5, 6, 7, 8, 9] else drawline(False) 30 # 第三步 31 drawline(True) if number in [0, 2, 3, 5, 6, 8, 9] else drawline(False) 32 # 第四步 33 drawline(True) if number in [0,1, 2, 6, 8] else drawline(False) 34 turtle.left(90) 35 # 第五步 36 drawline(True) if number in [0,1,4, 5, 6, 8, 9] else drawline(False) 37 # 第六步 38 drawline(True) if number in [0, 2, 3, 5, 6, 7, 8, 9] else drawline(False) 39 # 第七步 40 drawline(True) if number in [0, 2, 3, 4, 7, 8, 9] else drawline(False) 41 turtle.left(180) 42 #drawgap()是数字的一笔一画之间留一点空隙 43 def drawgap(): 44 turtle.penup() 45 turtle.fd(5) 46 #drawline(draw)draw为True或者False,控制一步画或者不画 47 def drawline(draw): 48 drawgap() 49 turtle.pendown() if draw else turtle.penup() 50 turtle.fd(40) 51 drawgap() 52 turtle.right(90) 53 import turtle 54 import random 55 import time 56 turtle.Turtle().screen.delay(0) 57 turtle.setup(800,400) 58 stopwatch(10)#输入秒数为10 59 turtle.done() 60 #注意:此方法进行计时误差太大,主要是因为turtle反应需要时间,不推荐使用
代码中有一处:
drawline(True) if number in [2, 3, 4, 5, 6, 8, 9] else drawline(False)
表达式1 if 判别式 else 表达式
这个表达式很有用,适合简短的if else语句
实例3:科赫雪花小包裹(来自第五周)
科赫曲线:
高大上的分形几何:是一种具有迭代关系的几何图形,广泛存在于自然界中。

简单来说可以理解为整体与局部具有很相似的结构
科赫曲线,也称为雪花曲线

雪花的局部与整体有一些相似性,这种相似性可以表达为科赫曲线的一种数学描述。
用python绘制科赫曲线
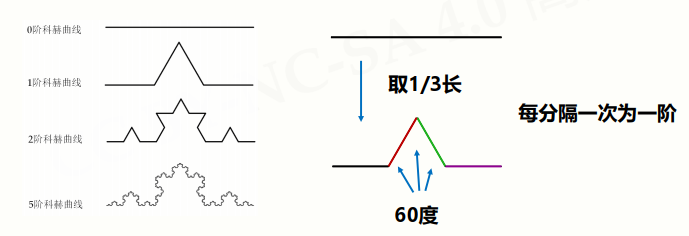
解释:取一条直线,取中间1/3的长度在中间形成一个等边三角形。同一个操作不断迭代,每分一次加一阶。
需达到的效果:输入阶数与原始长度,输出对应科赫曲线
方法:使用递归,同时使用turtle画图
思想:
递归 = 函数+分支;
递归链条:线段的组合;
当n为1时,也就是使用四次基例;当n为2时也就是在四次的基础上分成16次基例·······
递归基例:极端情况,n=0,画直线。
程序:
1 #demo2.py 2 def koch(n,size):#n是阶数,size是原始线段长度 3 # 递归基例 4 if n == 0 : 5 turtle.fd(size) 6 #递归链条 7 else : 8 for angle in [0,60,240,60]: 9 turtle.left(angle) 10 koch(n-1,size*(1/3)) 11 #主程序 12 import turtle 13 turtle.setup(800,400) 14 turtle.pencolor("blue") 15 turtle.pensize(2) 16 turtle.penup() 17 turtle.goto(-300,-100) 18 turtle.pendown() 19 koch(5,600) 20 turtle.done()

绘图时,可能绘图速度会很慢,可以使用如下代码:
1 turtle.speed(0) 2 '''参数0为最快,10为较快,6为正常,3为较慢,1为最慢''' 3 '''turtle.Turtle().screen.delay(0)即完全消除延迟'''
科赫曲线→科赫雪花
加入代码:
1 koch(4,300) 2 turtle.right(120) 3 koch(4,300) 4 turtle.right(120) 5 koch(4,300) 6 turtle.right(120) 7 turtle.done()

turtle.hideturtle()为隐藏画笔的turtle形状

深入理解函数递归的思想





 浙公网安备 33010602011771号
浙公网安备 33010602011771号