景区灭火问题——图像处理，最短路径

景区灭火问题

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

总结

一、图像预处理

　　首先，我们需要把图像转换成数值型数据，即二值化图像，得到只含有0（黑色）和1（白色）的逻辑矩阵，二值化图像中数据中数值为0的像素点显示黑色，数值为1的像素点显示未白色。

　　相关代码如下：

clc,clear,close all
RGB = imread('附件1（图像）.bmp');
RGB_gray = rgb2gray(RGB);         %灰度图像
BW1 = im2bw(RGB_gray);            %二值化图像

　　我们将得到的逻辑矩阵复制到Excel中，数值为0的像素点填充成黑色，白色像素点用空白显示，得到的部分图形如下：

 

 

二、图像分析与数据选取

 

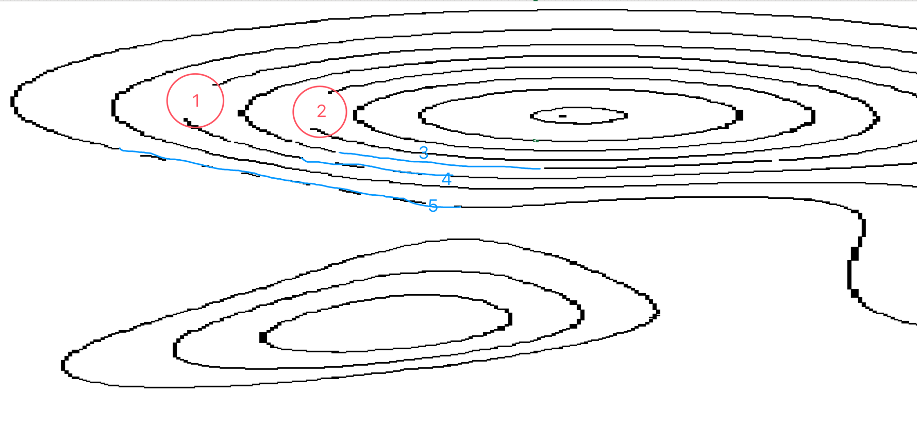
　　从Excel中绘制的相似图形可知，图像的缺失部分主要为1,2两个类似于二次函数的部分和3,4，5两个类似于直线的部分。

处理方法：(1)对于1,2两处曲线缺失部分，我们考虑使用函数拟合的方法进行修补复原

　　　　　(2)对于3,4，5三个类似于直线的部分，我们考虑用拉格朗日差值法进行修补复原

　　　　　通常对缺失数据进行补充，两种方法都可以选择，可以使用函数拟合和插值两种方法分别进行修复补充，将得到的结果进行比较。也可以用一种方法进行修复补充，用另一种方法进行检验，查看吻合度是否较高。

数据选取：为对缺失处进行修复，我们主要选取破损处附近的同一等高线上的点作为数据。

三、函数拟合

　　模型建立流程即原理公式见上文。

　　1，2两个缺口处的曲线与二次函数类似，可以用二次函数进行拟合。文章中，r(1)=1，r(2)=xi,r(3)=xi^2,即构建二次函数关系。

　　相关代码如下：

clc,clear,close all
load('data1.mat') %加载数据
x1 = [data1(2,1:end-1),data1(8,1:4)];%取点x（分行数据第一行）
y1 = [data1(3,1:end-1),data1(9,1:4)];%取点y（分行数据第一行）
x2 = [data1(8,5:end-1),data1(14,1:end)];%取点x（分行数据第二行）
y2 = [data1(9,5:end-1),data1(15,1:end)];%取点y（分行数据第二行）
plot([y1,y2],[x1,x2],'b.')　　　　%将分行数据连接起来，绘图
a = polyfit([y1,y2],[x1,x2],2);　　%二次函数拟合
y = min([y1,y2])-10:max([y1,y2])+10; %设置横坐标
x = a(1)*y.^2+a(2)*y+a(3);　　　　%拟合值
hold on
plot(y,x,'r.--','linewidth',2)　　%画图

　　可以用原始点和拟合的点计算RSS,MSE,RMSE等指标对拟合效果进行评价。

　　图形修复：取缺失范围内的整数点xi，得到对应拟合值（取整）yi。在二值化矩阵中将该点处的数值更改为0.

 

四、Lagrange插值（拉格朗日插值）

　　拉格朗日插值法的原理公式见上文。

 　　3,4,5三个缺口处的曲线与直线相近，利用拉格朗日插值法进行修复。

　　MATLAB中的插值函数为interp1，其调用格式为： yi= interp1(x,y,xi,'method')

　　其中x，y为插值点，yi为在被插值点xi处的插值结果；x,y为向量，'method'表示采用的插值方法，MATLAB提供的插值方法有几种：'nearest'是最邻近插值， 'linear'线性插值； 'spline'三次样条插值； 'pchip'立方插值．缺省时表示线性插值。注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。

　　相关代码如下：

%% matlab插值,图形修补
clc,clear,close all

a=imread('附件1（图像）.bmp');      %读入图像
figure('color',[1,1,1])           %图形背景设置为白色
subplot(121),imshow(a);title('原始图像')%绘制原始图像

%%一维插值方法
%对5号缺口处进行插值补充
x=[114,115,118,120,122,123,125,127,135,137,139,140,151,153,162,164,165,166,175,177,178,179,180,189,190,191,193,194,204,206,208,211,212,221,229,231,236,239,240,245,247];
y=[133,135,137,139,139,140,143,144,151,152,153,155,161,162,168,169,170,171,175,176,177,178,179,184,185,186,187,188,193,194,195,196,197,200,201,201,200,200,199,199,198];
j=1;
for i=114:247
    y1(1,j)=interp1(x,y,i,'cubic'); %立方差值，得到y1
    j=j+1;
end
x1=114:247;                         %x1取值
subplot(122)                        
imshow(a);
hold on;                           %在原始图像上添加
plot(x1,y1,'k');title('插值后图像')  %在5号缺口处补充数据

%对4号缺口处进行插值补充
clc,clear
x=[167,170,173,177,188,195,204,209,211,220,224,233];
y=[145,147,150,152,158,162,166,168,169,171,172,173];
j=1;
for i=167:233
    y1(1,j)=interp1(x,y,i,'cubic');%立方差值，得到y1
    j=j+1;
end
x1=167:233;                         %x1取值
hold on                             %在之前的图像上继续补充
plot(x1,y1,'k')                     %在4号缺口处补充数据

%对3号缺口处进行插值补充
clc,clear
x=[172,173,174,175,177,178,178.5,179,181,183,184,185,186,187,246,265,266,273,274,281,282,288];
y=[133,135,136,137,138,139,140,141,143,143,144,145,146,147,163,163,162,162,161,161,160,160];
j=1;
for i=172:288
    y1(1,j)=interp1(x,y,i,'cubic');     %立方差值，得到y1
    j=j+1;
end
x1=172:288;                             %x1取值
hold on                                 %在之前的图像上继续补充
plot(x1,y1,'k')                         %在3号缺口处补充数据

得到修复后的图像为：

　　　　　　　　　　　　　　　　　　

 

 

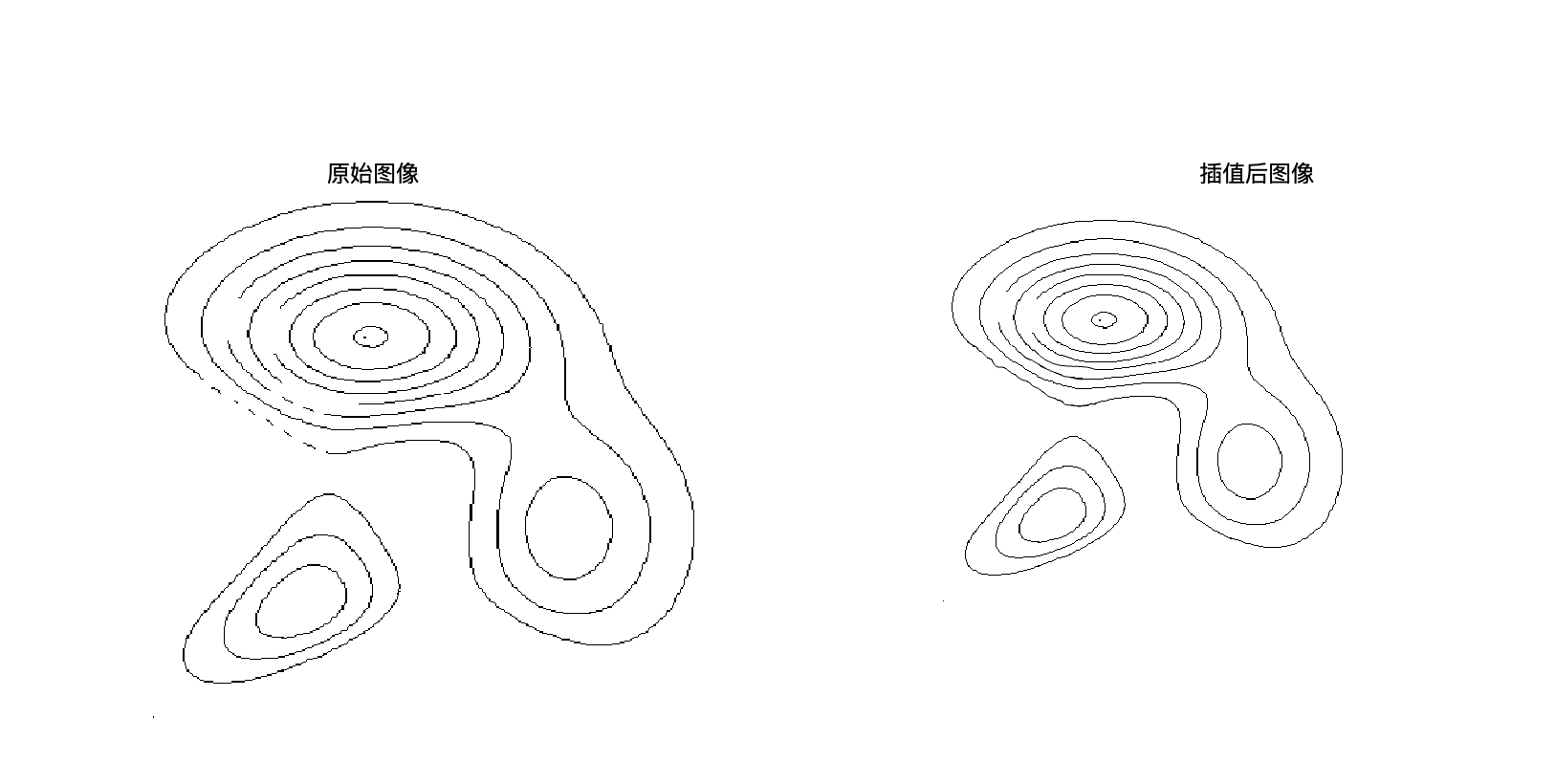
　　文章中数据的选取是以一段距离为间隔间隔取点，数据量较少，拟合插值效果可能不好，可以选择缺口附近的连续数据进行拟合插值，数据量更多，效果可能更好。

 

五、三维数据插值与图像绘制

　　本文采用三角形插值方法由已知点的坐标插值出其他点空间坐标。

　　三角形插值的模型建立和理论公式见上文。

meshgrid——二维和三维网格函数

　　用法：

　　（1）[X,Y] = meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维网格坐标。x，y互相为行列向量，若x是行向量，y是列向量，则得到的X 是一个矩阵，行数为向量y数据数length(y)，每一行是都与x相同；Y 也是一个矩阵，列数为向量x数据数length(x)，每一列是都与y相同，坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。

　　（2）[X,Y] = meshgrid(x) 与 [X,Y] = meshgrid(x,x) 相同，并返回网格大小为 length(x)×length(x) 的方形网格坐标。

　　（3）[X,Y,Z] = meshgrid(x,y,z) 返回由向量 x、y 和 z 定义的三维网格坐标。X、Y 和 Z 表示的网格的大小为 length(y)×length(x)×length(z)。

　　（3）[X,Y,Z] = meshgrid(x) 与 [X,Y,Z] = meshgrid(x,x,x) 相同，并返回网格大小为 length(x)×length(x)×length(x) 的三维网格坐标。

 

griddata——对二维或三维散点数据进行插值

　　用法：

　　(1)　ZI = griddata(x,y,z,XI,YI)
　　　　用二元函数z=f(x,y)的曲面拟合三维散点数据 (x,y,v)。griddata 将返回曲面z 在点（XI,YI）处的插值。曲面总是经过这些数据点（x,y,z）的。输入参量（XI,YI）通常是规则的格点（像用命令meshgrid 生成的一样）。XI 可以是一行向量，这时XI 指定一有常数列向量的矩阵。类似地，YI 可以是一列向量，它指定一有常数行向量的矩阵。
　　(2)[XI,YI,ZI] = griddata(x,y,z,xi,yi)
　　返回的矩阵ZI 的同时，返回的矩阵XI,YI 是由行向量xi 与列向量yi 用命令meshgrid 生成的。
　　(3)[XI,YI,ZI] = griddata(.......,method)
　　用指定的算法method 计算：
　　　　‘linear’：基于三角形的线性插值（缺省算法）；
　　　　‘cubic’： 基于三角形的三次插值；
　　　　‘nearest’：最邻近插值法；
　　　　‘v4’：MATLAB 4 中的griddata 算法。

 

pcolor——绘制伪彩图

　　用法：

　　pcolor(X,Y,C) 在X,Y定义的表格中用C填充颜色。C 的大小必须与 x-y 坐标网格的大小匹配，例如，如果 X 和 Y 定义一个 m×n 网格，则 C 必须为 m×n 矩阵。

 

contourf——填充二维等高线图

　用法：

　　contourf(X,Y,Z) 在X,Y定义的表格中Z值相同的点用等高线串连起来。C 的大小必须与 x-y 坐标网格的大小匹配，例如，如果 X 和 Y 定义一个 m×n 网格，则 C 必须为 m×n 矩阵。

 

surf——绘制曲面图

用法：

　　surf(X,Y,Z) 　创建一个三维曲面图，它是一个具有实色边和实色面的三维曲面。该函数将矩阵 Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。曲面的颜色根据 Z 指定的高度而变化。

　　surf(X,Y,Z,C) 　　C指定曲面的颜色。

 

例题完整代码如下：

%%三维插值法与曲面绘制
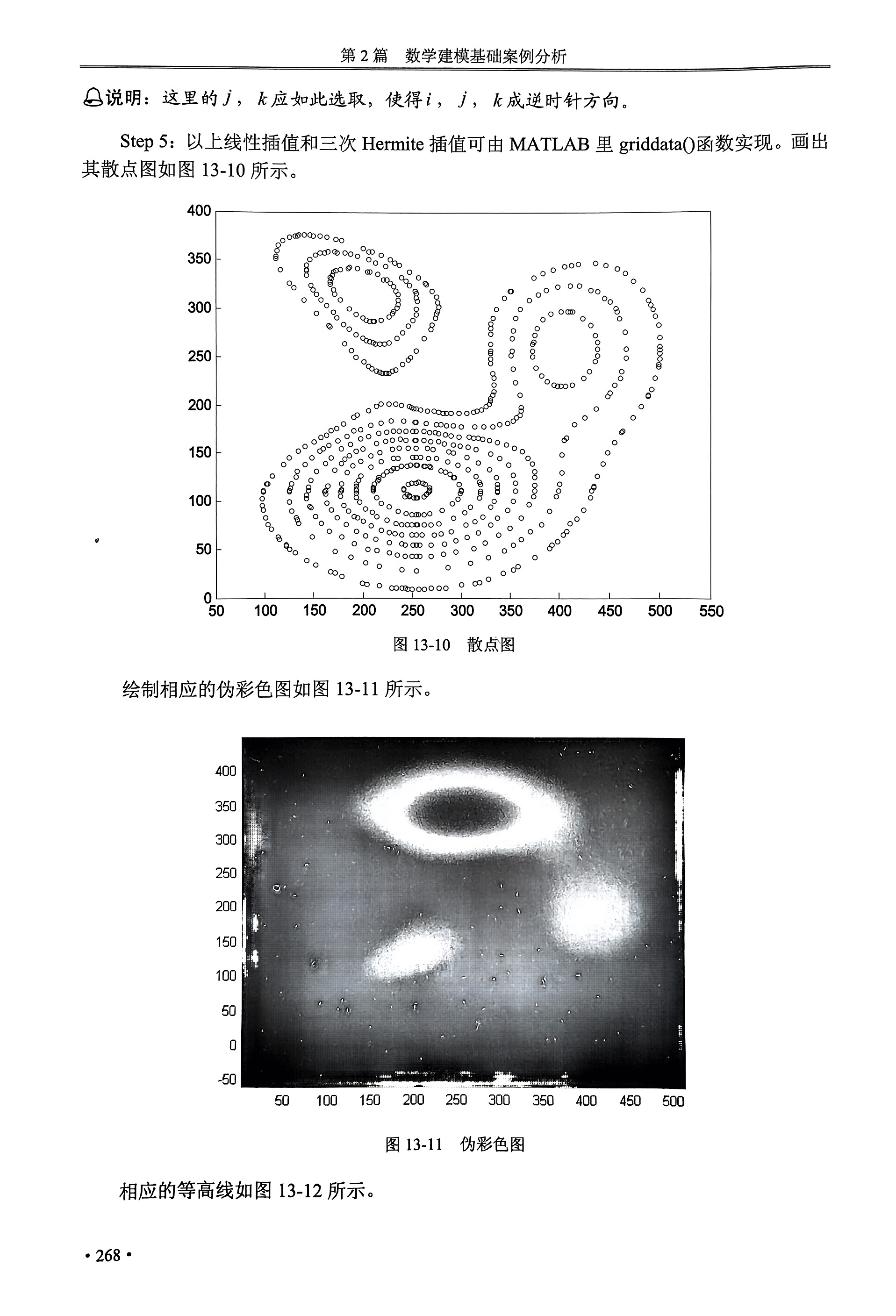
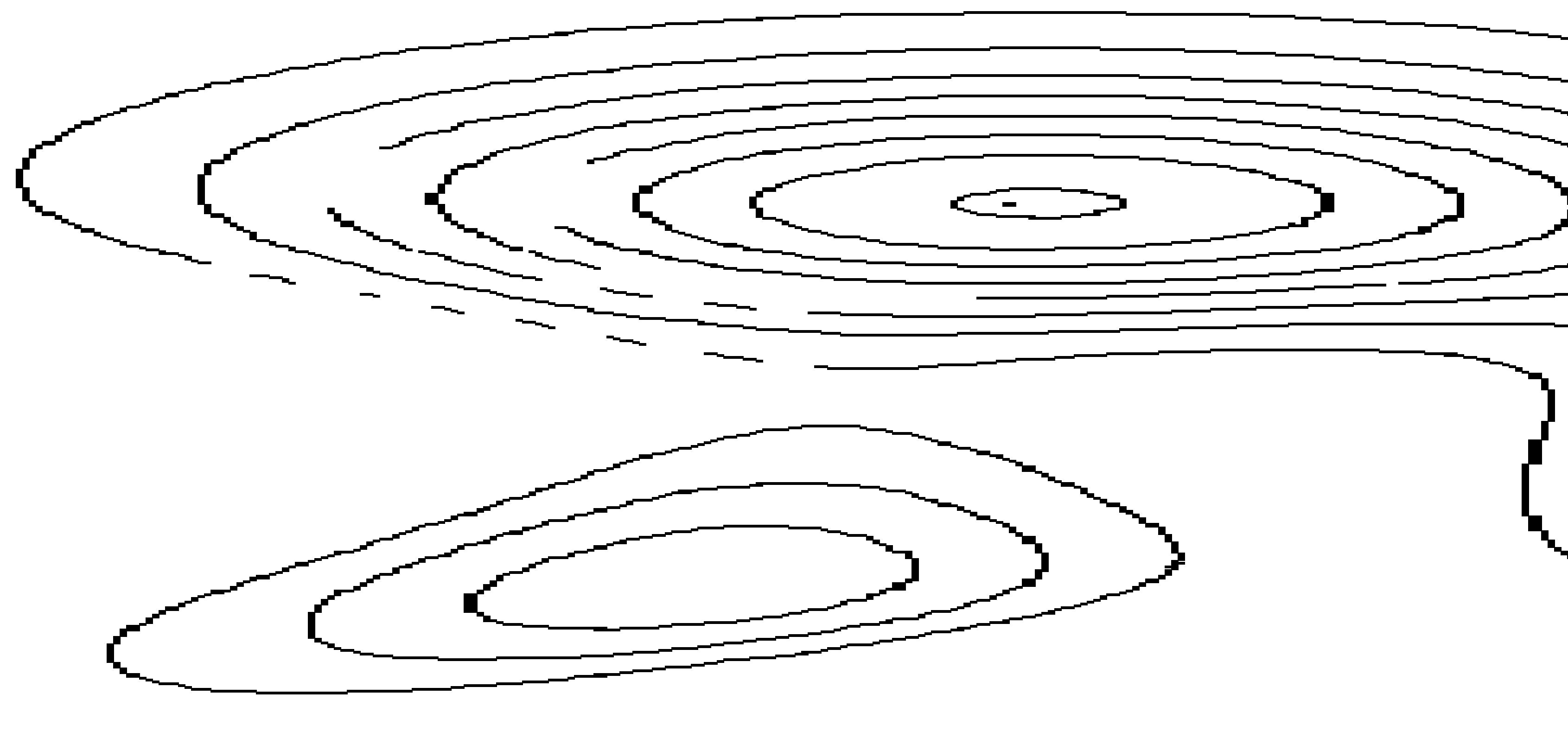
clc,clear,close all
A=[99,110,0;433,111,0;254,196,0;330,256,0;408,69,0;501,257,0;412,345,0;112,354,0;223,232,0;276,306,0;206,359,0;122,53,0;171,25,0;204,14,0;319,16,0;354,29,0;393,54,0;435,114,0;463,171,0;489,209,0;500,241,0;492,304,0;458,341,0;405,343,0;350,317,0;334,228,0;331,204,0;286,191,0;250,197,0;219,201,0;191,186,0;163,168,0;126,144,0;103,118,0;130,321,0;166,281,0;194,249,0;246,246,0;271,283,0;264,326,0;233,347,0;179,370,0;131,375,0;104,76,0;115,60,0;126,50,0;143,38,0;152,33,0;167,26,0;178,22,0;199,15,0;216,12,0;229,10,0;234,10,0;239,10,0;243,10,0;245,9,0;250,9,0;257,9,0;263,9,0;269,10,0;277,10,0;285,10,0;300,13,0;314,15,0;328,19,0;343,25,0;358,32,0;375,41,0;390,51,0;398,58,0;404,65,0;411,77,0;418,81,0;425,91,0;432,103,0;435,115,0;439,126,0;445,139,0;449,150,0;456,161,0;464,172,0;475,187,0;483,198,0;489,210,0;493,216,0;496,228,0;500,239,0;501,247,0;501,253,0;501,260,0;501,270,0;500,282,0;496,292,0;494,299,0;489,308,0;484,319,0;475,328,0;466,336,0;458,341,0;447,345,0;436,347,0;419,346,0;405,343,0;394,340,0;383,336,0;374,332,0;351,318,0;344,311,0;336,299,0;333,290,0;331,284,0;330,279,0;330,273,0;330,263,0;330,253,0;331,247,0;331,243,0;333,232,0;334,227,0;334,220,0;334,214,0;333,210,0;331,206,0;329,201,0;326,198,0;321,195,0;317,193,0;313,192,0;306,191,0;298,191,0;290,191,0;282,191,0;277,192,0;273,193,0;266,193,0;259,195,0;252,196,0;248,198,0;240,199,0;234,201,0;227,201,0;219,201,0;214,198,0;206,194,0;195,189,0;181,180,0;174,175,0;168,173,0;158,166,0;151,161,0;142,156,0;135,151,0;126,144,0;120,138,0;108,126,0;102,117,0;99,109,0;98,102,0;98,95,0;99,91,0;101,82,0;107,71,0;114,62,0;122,54,0;131,46,0;234,236,0;241,242,0;249,249,0;254,256,0;262,268,0;269,278,0;274,290,0;275,294,0;276,297,0;277,301,0;276,306,0;275,312,0;271,317,0;265,325,0;257,332,0;248,338,0;237,345,0;228,350,0;219,355,0;209,358,0;200,362,0;173,371,0;164,374,0;157,375,0;150,375,0;146,376,0;140,376,0;135,376,0;133,375,0;125,374,0;119,370,0;114,365,0;113,360,0;112,351,0;116,340,0;125,326,0;140,308,0;153,294,0;167,280,0;182,263,0;189,255,0;201,244,0;206,239,0;210,237,0;214,234,0;218,233,0;220,232,0;224,232,0;227,232,0;230,234,0;
126,111,50;254,28,50;400,111,50;254,182,50;352,256,50;408,166,50;468,258,50;411,323,50;143,339,50;218,263,50;256,307,50;206,350,50;133,80,50;149,63,50;171,47,50;188,41,50;203,36,50;216,32,50;240,29,50;287,31,50;310,36,50;328,42,50;344,48,50;354,54,50;362,60,50;371,68,50;382,76,50;390,90,50;397,105,50;401,118,50;403,129,50;403,148,50;405,163,50;416,179,50;426,187,50;438,196,50;449,209,50;456,220,50;463,234,50;468,249,50;467,275,50;461,290,50;457,300,50;451,307,50;439,317,50;452,212,50;462,228,50;468,249,50;467,275,50;458,297,50;446,311,50;432,319,50;420,323,50;398,322,50;387,319,50;379,314,50;370,308,50;361,299,50;356,289,50;354,277,50;352,268,50;351,251,50;353,237,50;356,223,50;361,210,50;362,197,50;362,193,50;361,189,50;357,186,50;353,183,50;348,181,50;340,179,50;333,177,50;324,177,50;314,177,50;300,177,50;293,178,50;286,178,50;280,179,50;275,180,50;265,181,50;253,182,50;242,183,50;229,183,50;219,181,50;208,178,50;198,174,50;191,172,50;184,167,50;175,162,50;166,157,50;160,154,50;156,151,50;149,144,50;142,138,50;134,130,50;132,125,50;128,118,50;127,113,50;126,109,50;126,99,50;128,89,50;132,82,50;135,77,50;222,263,50;227,264,50;235,268,50;241,274,50;246,281,50;251,287,50;254,293,50;255,299,50;256,307,50;255,311,50;254,315,50;253,318,50;248,323,50;244,328,50;240,332,50;223,343,50;213,347,50;206,350,50;195,354,50;188,356,50;182,357,50;174,357,50;171,358,50;165,358,50;161,357,50;156,357,50;152,355,50;146,350,50;143,345,50;143,340,50;143,334,50;147,323,50;150,319,50;153,314,50;158,308,50;164,302,50;170,295,50;174,290,50;181,283,50;187,278,50;194,272,50;200,268,50;204,266,50;207,265,50;211,264,50;213,263,50;218,263,50;
145,111,100;254,43,100;375,111,100;254,173,100;373,256,100;402,219,100;439,258,100;411,297,100;168,330,100;212,286,100;236,308,100;205,338,100;146,94,100;152,84,100;158,77,100;166,69,100;178,62,100;191,55,100;205,50,100;214,48,100;227,46,100;235,44,100;243,43,100;250,43,100;250,43,100;258,43,100;269,43,100;282,45,100;295,47,100;313,51,100;325,57,100;339,65,100;350,72,100;362,83,100;370,97,100;374,105,100;375,110,100;376,116,100;376,124,100;376,130,100;373,139,100;368,145,100;363,151,100;355,155,100;347,159,100;338,161,100;329,163,100;322,164,100;318,165,100;313,165,100;309,167,100;298,167,100;290,168,100;284,169,100;277,170,100;274,171,100;268,171,100;262,172,100;255,172,100;251,173,100;244,173,100;237,173,100;231,172,100;224,171,100;216,170,100;206,167,100;198,164,100;188,158,100;179,154,100;168,145,100;162,139,100;153,130,100;147,121,100;145,114,100;143,106,100;143,102,100;147,93,100;373,256,100;373,250,100;377,238,100;382,230,100;388,224,100;395,220,100;399,219,100;406,219,100;414,221,100;425,228,100;431,234,100;436,245,100;439,251,100;439,258,100;439,265,100;436,272,100;432,283,100;424,290,100;414,296,100;409,297,100;402,297,100;392,294,100;384,288,100;378,279,100;375,272,100;374,265,100;373,262,100;219,287,100;227,291,100;230,294,100;232,297,100;235,300,100;236,304,100;236,308,100;236,314,100;234,317,100;231,322,100;228,326,100;224,329,100;221,329,100;215,335,100;207,338,100;195,341,100;187,342,100;185,341,100;177,340,100;173,339,100;170,337,100;169,334,100;167,331,100;167,327,100;167,324,100;170,319,100;172,314,100;177,308,100;186,299,100;193,293,100;200,289,100;204,287,100;207,286,100;211,286,100;
162,111,150;254,54,150;356,111,150;254,163,150;162,107,150;164,98,150;168,91,150;174,82,150;183,75,150;193,68,150;203,64,150;213,60,150;227,57,150;239,55,150;243,54,150;251,54,150;258,54,150;269,54,150;283,56,150;295,59,150;306,63,150;318,67,150;330,75,150;338,82,150;348,91,150;353,100,150;356,110,150;356,119,150;354,127,150;349,137,150;340,144,150;331,149,150;316,154,150;308,156,150;299,157,150;292,159,150;283,160,150;277,162,150;270,162,150;263,163,150;253,163,150;244,163,150;238,164,150;230,163,150;223,162,150;214,160,150;200,154,150;194,151,150;187,147,150;182,143,150;178,139,150;171,131,150;165,115,150;162,111,150;161,109,150;
178,112,200;254,65,200;337,111,200;254,155,200;177,105,200;181,95,200;185,90,200;191,84,200;195,83,200;200,79,200;208,74,200;219,70,200;227,67,200;233,66,200;240,65,200;250,65,200;260,65,200;273,65,200;280,66,200;290,69,200;305,75,200;314,79,200;322,84,200;330,94,200;334,100,200;337,109,200;338,114,200;338,117,200;336,124,200;329,133,200;318,140,200;306,146,200;293,150,200;288,151,200;272,154,200;266,155,200;246,155,200;237,155,200;230,154,200;218,150,200;208,147,200;198,141,200;190,136,200;184,129,200;179,118,200;178,111,200;177,109,200;
193,112,250;254,75,250;320,111,250;254,146,250;193,108,250;194,104,250;197,99,250;203,92,250;209,88,250;214,84,250;225,80,250;234,77,250;240,76,250;245,76,250;250,75,250;256,75,250;263,75,250;269,76,250;277,77,250;292,82,250;304,88,250;310,94,250;319,104,250;320,108,250;320,117,250;319,120,250;315,126,250;307,133,250;297,138,250;287,141,250;275,144,250;267,145,250;259,146,250;251,146,250;236,145,250;231,144,250;219,141,250;208,135,250;198,126,250;196,121,250;194,117,250;193,115,250;193,111,250;
211,112,300;254,86,300;300,111,300;254,137,300;211,111,300;214,104,300;219,98,300;227,94,300;236,89,300;244,87,300;250,86,300;257,86,300;263,86,300;268,87,300;281,91,300;291,98,300;297,102,300;299,108,300;300,112,300;298,117,300;293,125,300;269,135,300;262,136,300;256,137,300;216,122,300;212,117,300;211,113,300;294,124,300;289,128,300;285,130,300;280,132,300;268,136,300;264,136,300;249,137,300;245,136,300;240,136,300;235,134,300;232,134,300;229,132,300;225,130,300;221,127,300;217,124,300;215,121,300;212,118,300;211,114,300;
242,113,350;254,104,350;268,112,350;254,119,350;242,112,350;245,107,350;248,106,350;252,104,350;256,104,350;262,105,350;265,107,350;267,109,350;268,111,350;268,114,350;264,117,350;261,119,350;257,120,350;254,119,350;250,119,350;246,118,350;243,105,350;242,113,350;248,105,350];

x=A(:,1);y=A(:,2);z=A(:,3);
scatter(x,y,5,z)    %绘制气泡散点图（点用圆形表示），5确定圆的面积，z确定圆的颜色

%% griddata：对二维或三维散点数据进行插值处理
figure('color',[1,1,1])                                       %图形背景设置为白色
[X,Y,Z]=griddata(x,y,z,linspace(1,512)',linspace(1,512),'v4');%三维数据插值，linespce函数默认分成100份
n1=size(Y);
for i=1:n1(1,1)             
    for j=1:n1(1,2)         
        Y(i,j)=512-Y(i,j); %调整y轴朝向
    end
end


n=size(Z);
for i=1:n(1,1)         
    for j=1:n(1,2)      
        if Z(i,j)<=0        %高度小于0的位置填充为0
            Z(i,j)=0;
        end
    end
end
pcolor(X,Y,Z);              %伪彩色图。在（X,Y)的网格中按Z填充颜色
shading interp              %消除网格线

%%绘制等高线图和三维曲面
figure,
contourf(X,Y,Z)     %等高线图
figure('color',[1,1,1]),
surf(X,Y,Z)         %三维曲面

 

 

六、曲面面积求解——微分法

　　为求解曲面的面积，利用微分法抽取其中三维曲面的一个小面积块来分析，绘制相应的小块图形并计算其面积，程序如下：

　　plot3——绘制3维点或线。

%% 得到曲面上所以点的坐标

clc,clear,close all

A=[99,110,0;433,111,0;254,196,0;330,256,0;408,69,0;501,257,0;412,345,0;112,354,0;223,232,0;276,306,0;206,359,0;122,53,0;171,25,0;204,14,0;319,16,0;354,29,0;393,54,0;435,114,0;463,171,0;489,209,0;500,241,0;492,304,0;458,341,0;405,343,0;350,317,0;334,228,0;331,204,0;286,191,0;250,197,0;219,201,0;191,186,0;163,168,0;126,144,0;103,118,0;130,321,0;166,281,0;194,249,0;246,246,0;271,283,0;264,326,0;233,347,0;179,370,0;131,375,0;104,76,0;115,60,0;126,50,0;143,38,0;152,33,0;167,26,0;178,22,0;199,15,0;216,12,0;229,10,0;234,10,0;239,10,0;243,10,0;245,9,0;250,9,0;257,9,0;263,9,0;269,10,0;277,10,0;285,10,0;300,13,0;314,15,0;328,19,0;343,25,0;358,32,0;375,41,0;390,51,0;398,58,0;404,65,0;411,77,0;418,81,0;425,91,0;432,103,0;435,115,0;439,126,0;445,139,0;449,150,0;456,161,0;464,172,0;475,187,0;483,198,0;489,210,0;493,216,0;496,228,0;500,239,0;501,247,0;501,253,0;501,260,0;501,270,0;500,282,0;496,292,0;494,299,0;489,308,0;484,319,0;475,328,0;466,336,0;458,341,0;447,345,0;436,347,0;419,346,0;405,343,0;394,340,0;383,336,0;374,332,0;351,318,0;344,311,0;336,299,0;333,290,0;331,284,0;330,279,0;330,273,0;330,263,0;330,253,0;331,247,0;331,243,0;333,232,0;334,227,0;334,220,0;334,214,0;333,210,0;331,206,0;329,201,0;326,198,0;321,195,0;317,193,0;313,192,0;306,191,0;298,191,0;290,191,0;282,191,0;277,192,0;273,193,0;266,193,0;259,195,0;252,196,0;248,198,0;240,199,0;234,201,0;227,201,0;219,201,0;214,198,0;206,194,0;195,189,0;181,180,0;174,175,0;168,173,0;158,166,0;151,161,0;142,156,0;135,151,0;126,144,0;120,138,0;108,126,0;102,117,0;99,109,0;98,102,0;98,95,0;99,91,0;101,82,0;107,71,0;114,62,0;122,54,0;131,46,0;234,236,0;241,242,0;249,249,0;254,256,0;262,268,0;269,278,0;274,290,0;275,294,0;276,297,0;277,301,0;276,306,0;275,312,0;271,317,0;265,325,0;257,332,0;248,338,0;237,345,0;228,350,0;219,355,0;209,358,0;200,362,0;173,371,0;164,374,0;157,375,0;150,375,0;146,376,0;140,376,0;135,376,0;133,375,0;125,374,0;119,370,0;114,365,0;113,360,0;112,351,0;116,340,0;125,326,0;140,308,0;153,294,0;167,280,0;182,263,0;189,255,0;201,244,0;206,239,0;210,237,0;214,234,0;218,233,0;220,232,0;224,232,0;227,232,0;230,234,0;
126,111,50;254,28,50;400,111,50;254,182,50;352,256,50;408,166,50;468,258,50;411,323,50;143,339,50;218,263,50;256,307,50;206,350,50;133,80,50;149,63,50;171,47,50;188,41,50;203,36,50;216,32,50;240,29,50;287,31,50;310,36,50;328,42,50;344,48,50;354,54,50;362,60,50;371,68,50;382,76,50;390,90,50;397,105,50;401,118,50;403,129,50;403,148,50;405,163,50;416,179,50;426,187,50;438,196,50;449,209,50;456,220,50;463,234,50;468,249,50;467,275,50;461,290,50;457,300,50;451,307,50;439,317,50;452,212,50;462,228,50;468,249,50;467,275,50;458,297,50;446,311,50;432,319,50;420,323,50;398,322,50;387,319,50;379,314,50;370,308,50;361,299,50;356,289,50;354,277,50;352,268,50;351,251,50;353,237,50;356,223,50;361,210,50;362,197,50;362,193,50;361,189,50;357,186,50;353,183,50;348,181,50;340,179,50;333,177,50;324,177,50;314,177,50;300,177,50;293,178,50;286,178,50;280,179,50;275,180,50;265,181,50;253,182,50;242,183,50;229,183,50;219,181,50;208,178,50;198,174,50;191,172,50;184,167,50;175,162,50;166,157,50;160,154,50;156,151,50;149,144,50;142,138,50;134,130,50;132,125,50;128,118,50;127,113,50;126,109,50;126,99,50;128,89,50;132,82,50;135,77,50;222,263,50;227,264,50;235,268,50;241,274,50;246,281,50;251,287,50;254,293,50;255,299,50;256,307,50;255,311,50;254,315,50;253,318,50;248,323,50;244,328,50;240,332,50;223,343,50;213,347,50;206,350,50;195,354,50;188,356,50;182,357,50;174,357,50;171,358,50;165,358,50;161,357,50;156,357,50;152,355,50;146,350,50;143,345,50;143,340,50;143,334,50;147,323,50;150,319,50;153,314,50;158,308,50;164,302,50;170,295,50;174,290,50;181,283,50;187,278,50;194,272,50;200,268,50;204,266,50;207,265,50;211,264,50;213,263,50;218,263,50;
145,111,100;254,43,100;375,111,100;254,173,100;373,256,100;402,219,100;439,258,100;411,297,100;168,330,100;212,286,100;236,308,100;205,338,100;146,94,100;152,84,100;158,77,100;166,69,100;178,62,100;191,55,100;205,50,100;214,48,100;227,46,100;235,44,100;243,43,100;250,43,100;250,43,100;258,43,100;269,43,100;282,45,100;295,47,100;313,51,100;325,57,100;339,65,100;350,72,100;362,83,100;370,97,100;374,105,100;375,110,100;376,116,100;376,124,100;376,130,100;373,139,100;368,145,100;363,151,100;355,155,100;347,159,100;338,161,100;329,163,100;322,164,100;318,165,100;313,165,100;309,167,100;298,167,100;290,168,100;284,169,100;277,170,100;274,171,100;268,171,100;262,172,100;255,172,100;251,173,100;244,173,100;237,173,100;231,172,100;224,171,100;216,170,100;206,167,100;198,164,100;188,158,100;179,154,100;168,145,100;162,139,100;153,130,100;147,121,100;145,114,100;143,106,100;143,102,100;147,93,100;373,256,100;373,250,100;377,238,100;382,230,100;388,224,100;395,220,100;399,219,100;406,219,100;414,221,100;425,228,100;431,234,100;436,245,100;439,251,100;439,258,100;439,265,100;436,272,100;432,283,100;424,290,100;414,296,100;409,297,100;402,297,100;392,294,100;384,288,100;378,279,100;375,272,100;374,265,100;373,262,100;219,287,100;227,291,100;230,294,100;232,297,100;235,300,100;236,304,100;236,308,100;236,314,100;234,317,100;231,322,100;228,326,100;224,329,100;221,329,100;215,335,100;207,338,100;195,341,100;187,342,100;185,341,100;177,340,100;173,339,100;170,337,100;169,334,100;167,331,100;167,327,100;167,324,100;170,319,100;172,314,100;177,308,100;186,299,100;193,293,100;200,289,100;204,287,100;207,286,100;211,286,100;
162,111,150;254,54,150;356,111,150;254,163,150;162,107,150;164,98,150;168,91,150;174,82,150;183,75,150;193,68,150;203,64,150;213,60,150;227,57,150;239,55,150;243,54,150;251,54,150;258,54,150;269,54,150;283,56,150;295,59,150;306,63,150;318,67,150;330,75,150;338,82,150;348,91,150;353,100,150;356,110,150;356,119,150;354,127,150;349,137,150;340,144,150;331,149,150;316,154,150;308,156,150;299,157,150;292,159,150;283,160,150;277,162,150;270,162,150;263,163,150;253,163,150;244,163,150;238,164,150;230,163,150;223,162,150;214,160,150;200,154,150;194,151,150;187,147,150;182,143,150;178,139,150;171,131,150;165,115,150;162,111,150;161,109,150;
178,112,200;254,65,200;337,111,200;254,155,200;177,105,200;181,95,200;185,90,200;191,84,200;195,83,200;200,79,200;208,74,200;219,70,200;227,67,200;233,66,200;240,65,200;250,65,200;260,65,200;273,65,200;280,66,200;290,69,200;305,75,200;314,79,200;322,84,200;330,94,200;334,100,200;337,109,200;338,114,200;338,117,200;336,124,200;329,133,200;318,140,200;306,146,200;293,150,200;288,151,200;272,154,200;266,155,200;246,155,200;237,155,200;230,154,200;218,150,200;208,147,200;198,141,200;190,136,200;184,129,200;179,118,200;178,111,200;177,109,200;
193,112,250;254,75,250;320,111,250;254,146,250;193,108,250;194,104,250;197,99,250;203,92,250;209,88,250;214,84,250;225,80,250;234,77,250;240,76,250;245,76,250;250,75,250;256,75,250;263,75,250;269,76,250;277,77,250;292,82,250;304,88,250;310,94,250;319,104,250;320,108,250;320,117,250;319,120,250;315,126,250;307,133,250;297,138,250;287,141,250;275,144,250;267,145,250;259,146,250;251,146,250;236,145,250;231,144,250;219,141,250;208,135,250;198,126,250;196,121,250;194,117,250;193,115,250;193,111,250;
211,112,300;254,86,300;300,111,300;254,137,300;211,111,300;214,104,300;219,98,300;227,94,300;236,89,300;244,87,300;250,86,300;257,86,300;263,86,300;268,87,300;281,91,300;291,98,300;297,102,300;299,108,300;300,112,300;298,117,300;293,125,300;269,135,300;262,136,300;256,137,300;216,122,300;212,117,300;211,113,300;294,124,300;289,128,300;285,130,300;280,132,300;268,136,300;264,136,300;249,137,300;245,136,300;240,136,300;235,134,300;232,134,300;229,132,300;225,130,300;221,127,300;217,124,300;215,121,300;212,118,300;211,114,300;
242,113,350;254,104,350;268,112,350;254,119,350;242,112,350;245,107,350;248,106,350;252,104,350;256,104,350;262,105,350;265,107,350;267,109,350;268,111,350;268,114,350;264,117,350;261,119,350;257,120,350;254,119,350;250,119,350;246,118,350;243,105,350;242,113,350;248,105,350];

x=A(:,1);y=A(:,2);z=A(:,3);

[X,Y,Z]=griddata(x,y,z,linspace(1,512)',linspace(1,512),'v4');%插值

n1=size(Y);

for i=1:n1(1,1)

　　for j=1:n1(1,2)

　　　　Y(i,j)=450-Y(i,j);

　　end

end

n=size(Z);

for i=1:n(1,1)

　　for j=1:n(1,2)

　　　　if Z(i,j)<=0

　　　　　　Z(i,j)=0;

　　　　end

　　end

end

figure('color',[1,1,1]),

surf(X,Y,Z)%三维曲面

xlabel('X');ylabel('Y');zlabel('Z')

%% 计算小立面格子面积
% 提取三维曲面的一个小面积块
figure('color',[1,1,1]),
x1 = 238.4; y1 = 314.8; z1 = 300.9;         %找点，二横纵坐标自由选取（最好根据图像大小选点构成正方形），z由插值的曲面函数求出。
x2 = 238.4; y2 = 309.6; z2 = 277.4;
x3 = 243.6; y3 = 314.8; z3 = 303.2;
x4 = 243.6; y4 = 309.6; z4 = 280.2;
plot3(x1,y1,z1,'ro');
hold on
plot3(x2,y2,z2,'ro');                       %绘点
plot3(x3,y3,z3,'ro');
plot3(x4,y4,z4,'ro');
plot3([x2,x4],[y2,y4],[z2,z4],'r-','linewidth',2);  %连线
plot3([x1,x2],[y1,y2],[z1,z2],'r-','linewidth',2);
plot3([x1,x2],[y1,y2],[z1,z2],'r-','linewidth',2);
plot3([x1,x3],[y1,y3],[z1,z3],'r-','linewidth',2);
plot3([x4,x3],[y4,y3],[z4,z3],'r-','linewidth',2);
fill3([x1,x2,x3,x4],[y1,y2,y3,y4],[z1,z2,z3,z4],'b') % 填充蓝色
fill3([x1,x3,x2,x4],[y1,y3,y2,y4],[z1,z3,z2,z4],'b') % 填充蓝色
%计算小面积块面积
a = sqrt((y1-y2)^2+(z1-z2)^2); % 边长a
b = sqrt((x2-x4)^2+(z2-z4)^2); % 边长b
S = a*b;  % 立面面积

得到图形：

 

 

　　统计图像中高度大于0的点数即可计算相应的地表面积，代码如下：

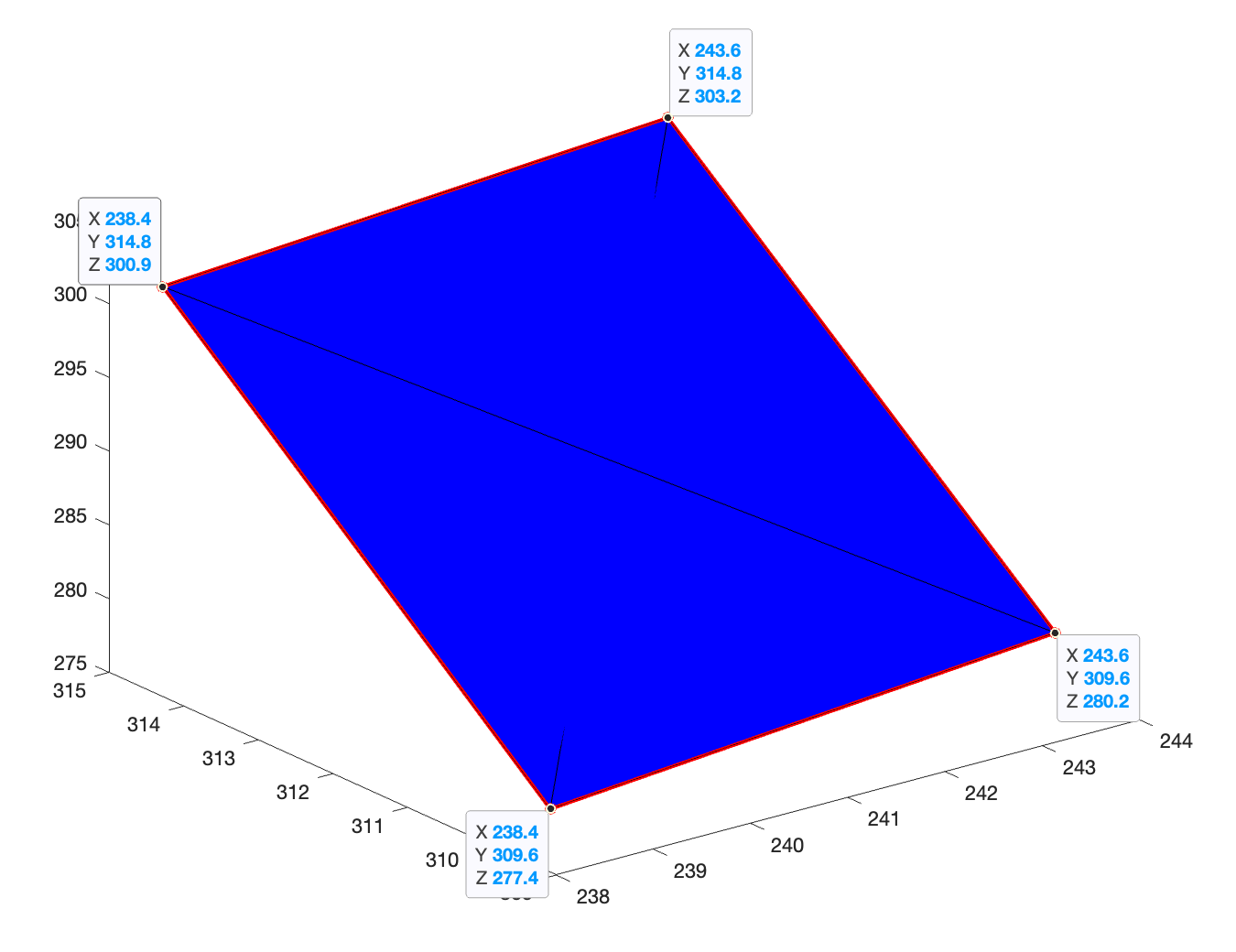
%% 统计点数（小面积块个数），计算表面积
num =0 ; % 计数器
n = size(X);
for i=1:n(1,1)
    for j=1:n(1,2)          
        if Z(i,j)>0         %高度大于0的点数
            num = num +1;   %统计个数
        end
    end
end
Ss = S*num/2   % 总的地表面积

 

七、最短路径问题

　　最短路径问题可以转化为已知函数某点，按最快速度下降原理求解函数的最小值的迭代问题，记录下每次迭代下点的值，则有这些点构成的路径就是最佳灭火路线。

　　最短路径函数代码：

function [r_path, r_cost] = dijkstra(pathS, pathE, transmat)
%  The Implemented Dijkstra's algorithm
%   pathS: 所求最短路径的起点
%   pathE :所求最短路径的终点
%   transmat: 图的转移矩阵或者邻接矩阵，应为方阵
if ( size(transmat,1) ~= size(transmat,2) )
  error( 'detect_cycles:Dijkstra_SC', ...
         'transmat has different width and heights' );
end

% 初始化:
%  noOfNode-图中的顶点数
%  parent(i)-节点i的父节点
%  distance(i)-从起点pathS的最短路径的长度
%  queue-图的广度遍历
noOfNode = size(transmat, 1);
 
for i = 1:noOfNode
  parent(i) = 0;
  distance(i) = Inf;
end
queue = [];

% Start from pathS
%
for i=1:noOfNode
  if transmat(pathS, i)~=Inf 
    distance(i) = transmat(pathS, i);
    parent(i)   = pathS;
    queue       = [queue i];
  end
end

% 对图进行广度遍历
while length(queue) ~= 0
  hopS  = queue(1);
  queue = queue(2:end);
  
  for hopE = 1:noOfNode
    if distance(hopE) > distance(hopS) + transmat(hopS,hopE)
      distance(hopE) = distance(hopS) + transmat(hopS,hopE);
      parent(hopE)   = hopS;
      queue          = [queue hopE];
    end
  end
  
end

% 回溯进行最短路径的查找
r_path = [pathE];    
i = parent(pathE);

while i~=pathS && i~=0
  r_path = [i r_path];
  i      = parent(i);
end
 
if i==pathS
  r_path = [i r_path];
else
  r_path = []
end

% 返回最短路径的权和
r_cost = distance(pathE);

应用到本题中的相关代码如下：

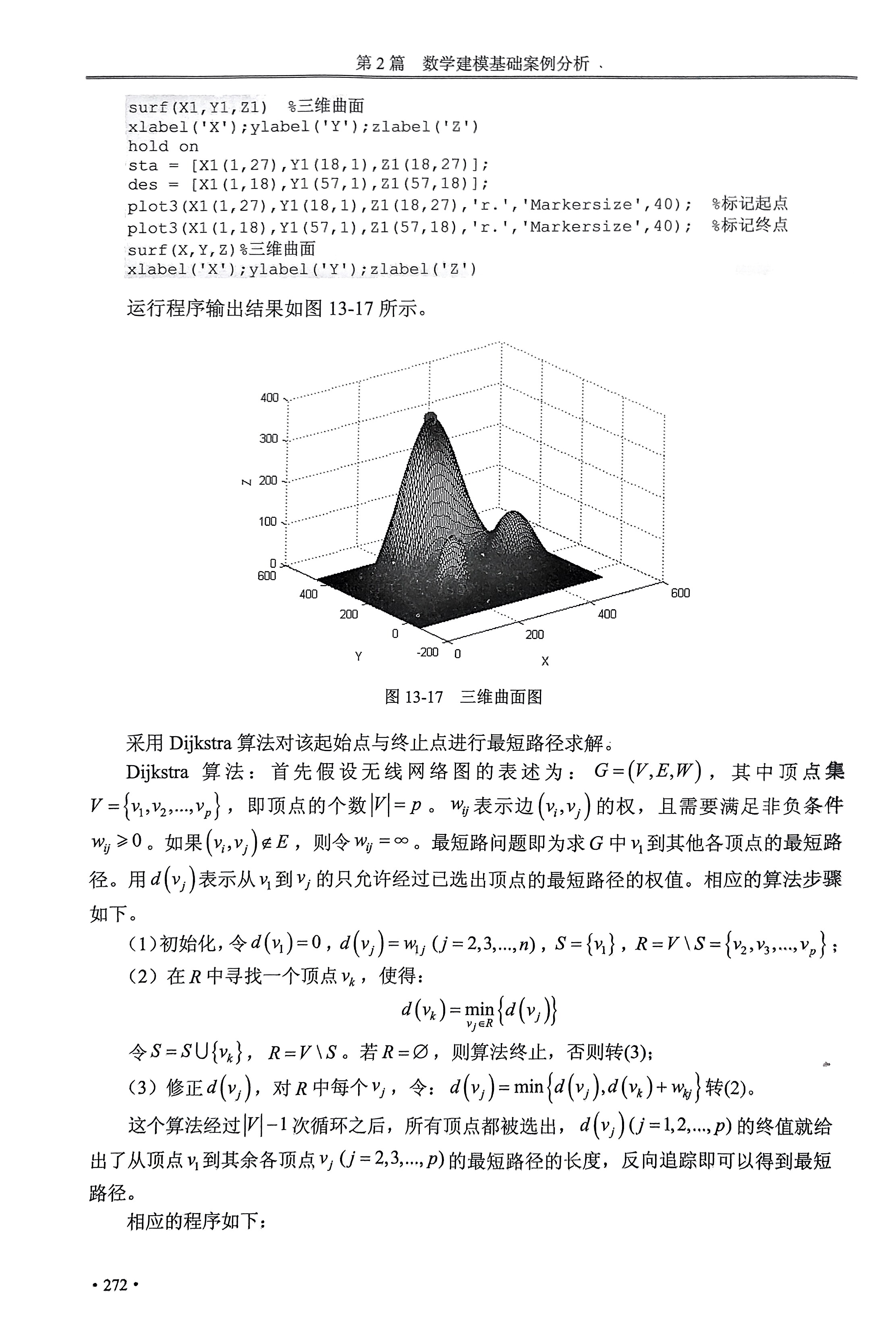
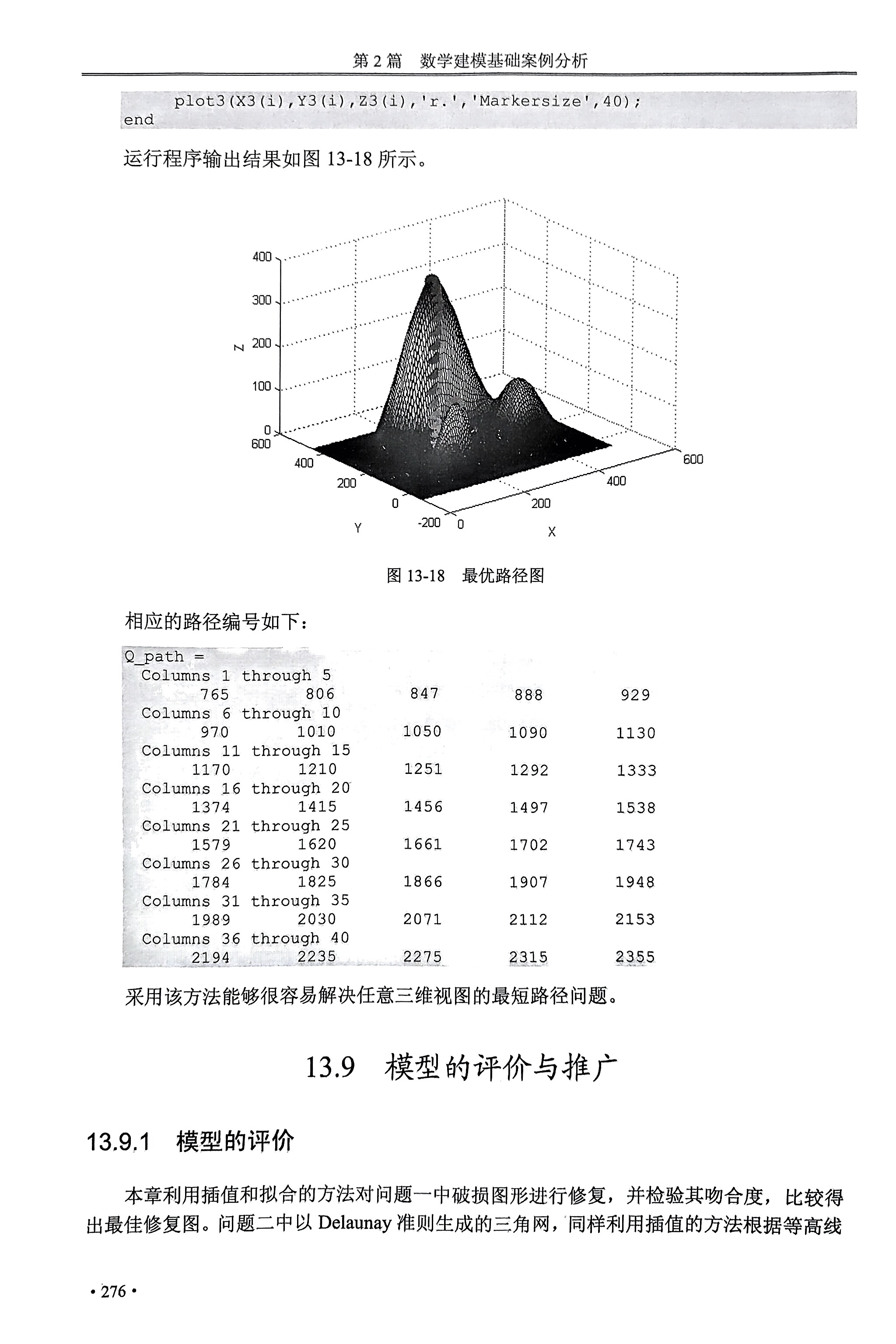
%% 最优路径
clc,clear,close all
A=[99,110,0;433,111,0;254,196,0;330,256,0;408,69,0;501,257,0;412,345,0;112,354,0;223,232,0;276,306,0;206,359,0;122,53,0;171,25,0;204,14,0;319,16,0;354,29,0;393,54,0;435,114,0;463,171,0;489,209,0;500,241,0;492,304,0;458,341,0;405,343,0;350,317,0;334,228,0;331,204,0;286,191,0;250,197,0;219,201,0;191,186,0;163,168,0;126,144,0;103,118,0;130,321,0;166,281,0;194,249,0;246,246,0;271,283,0;264,326,0;233,347,0;179,370,0;131,375,0;104,76,0;115,60,0;126,50,0;143,38,0;152,33,0;167,26,0;178,22,0;199,15,0;216,12,0;229,10,0;234,10,0;239,10,0;243,10,0;245,9,0;250,9,0;257,9,0;263,9,0;269,10,0;277,10,0;285,10,0;300,13,0;314,15,0;328,19,0;343,25,0;358,32,0;375,41,0;390,51,0;398,58,0;404,65,0;411,77,0;418,81,0;425,91,0;432,103,0;435,115,0;439,126,0;445,139,0;449,150,0;456,161,0;464,172,0;475,187,0;483,198,0;489,210,0;493,216,0;496,228,0;500,239,0;501,247,0;501,253,0;501,260,0;501,270,0;500,282,0;496,292,0;494,299,0;489,308,0;484,319,0;475,328,0;466,336,0;458,341,0;447,345,0;436,347,0;419,346,0;405,343,0;394,340,0;383,336,0;374,332,0;351,318,0;344,311,0;336,299,0;333,290,0;331,284,0;330,279,0;330,273,0;330,263,0;330,253,0;331,247,0;331,243,0;333,232,0;334,227,0;334,220,0;334,214,0;333,210,0;331,206,0;329,201,0;326,198,0;321,195,0;317,193,0;313,192,0;306,191,0;298,191,0;290,191,0;282,191,0;277,192,0;273,193,0;266,193,0;259,195,0;252,196,0;248,198,0;240,199,0;234,201,0;227,201,0;219,201,0;214,198,0;206,194,0;195,189,0;181,180,0;174,175,0;168,173,0;158,166,0;151,161,0;142,156,0;135,151,0;126,144,0;120,138,0;108,126,0;102,117,0;99,109,0;98,102,0;98,95,0;99,91,0;101,82,0;107,71,0;114,62,0;122,54,0;131,46,0;234,236,0;241,242,0;249,249,0;254,256,0;262,268,0;269,278,0;274,290,0;275,294,0;276,297,0;277,301,0;276,306,0;275,312,0;271,317,0;265,325,0;257,332,0;248,338,0;237,345,0;228,350,0;219,355,0;209,358,0;200,362,0;173,371,0;164,374,0;157,375,0;150,375,0;146,376,0;140,376,0;135,376,0;133,375,0;125,374,0;119,370,0;114,365,0;113,360,0;112,351,0;116,340,0;125,326,0;140,308,0;153,294,0;167,280,0;182,263,0;189,255,0;201,244,0;206,239,0;210,237,0;214,234,0;218,233,0;220,232,0;224,232,0;227,232,0;230,234,0;
126,111,50;254,28,50;400,111,50;254,182,50;352,256,50;408,166,50;468,258,50;411,323,50;143,339,50;218,263,50;256,307,50;206,350,50;133,80,50;149,63,50;171,47,50;188,41,50;203,36,50;216,32,50;240,29,50;287,31,50;310,36,50;328,42,50;344,48,50;354,54,50;362,60,50;371,68,50;382,76,50;390,90,50;397,105,50;401,118,50;403,129,50;403,148,50;405,163,50;416,179,50;426,187,50;438,196,50;449,209,50;456,220,50;463,234,50;468,249,50;467,275,50;461,290,50;457,300,50;451,307,50;439,317,50;452,212,50;462,228,50;468,249,50;467,275,50;458,297,50;446,311,50;432,319,50;420,323,50;398,322,50;387,319,50;379,314,50;370,308,50;361,299,50;356,289,50;354,277,50;352,268,50;351,251,50;353,237,50;356,223,50;361,210,50;362,197,50;362,193,50;361,189,50;357,186,50;353,183,50;348,181,50;340,179,50;333,177,50;324,177,50;314,177,50;300,177,50;293,178,50;286,178,50;280,179,50;275,180,50;265,181,50;253,182,50;242,183,50;229,183,50;219,181,50;208,178,50;198,174,50;191,172,50;184,167,50;175,162,50;166,157,50;160,154,50;156,151,50;149,144,50;142,138,50;134,130,50;132,125,50;128,118,50;127,113,50;126,109,50;126,99,50;128,89,50;132,82,50;135,77,50;222,263,50;227,264,50;235,268,50;241,274,50;246,281,50;251,287,50;254,293,50;255,299,50;256,307,50;255,311,50;254,315,50;253,318,50;248,323,50;244,328,50;240,332,50;223,343,50;213,347,50;206,350,50;195,354,50;188,356,50;182,357,50;174,357,50;171,358,50;165,358,50;161,357,50;156,357,50;152,355,50;146,350,50;143,345,50;143,340,50;143,334,50;147,323,50;150,319,50;153,314,50;158,308,50;164,302,50;170,295,50;174,290,50;181,283,50;187,278,50;194,272,50;200,268,50;204,266,50;207,265,50;211,264,50;213,263,50;218,263,50;
145,111,100;254,43,100;375,111,100;254,173,100;373,256,100;402,219,100;439,258,100;411,297,100;168,330,100;212,286,100;236,308,100;205,338,100;146,94,100;152,84,100;158,77,100;166,69,100;178,62,100;191,55,100;205,50,100;214,48,100;227,46,100;235,44,100;243,43,100;250,43,100;250,43,100;258,43,100;269,43,100;282,45,100;295,47,100;313,51,100;325,57,100;339,65,100;350,72,100;362,83,100;370,97,100;374,105,100;375,110,100;376,116,100;376,124,100;376,130,100;373,139,100;368,145,100;363,151,100;355,155,100;347,159,100;338,161,100;329,163,100;322,164,100;318,165,100;313,165,100;309,167,100;298,167,100;290,168,100;284,169,100;277,170,100;274,171,100;268,171,100;262,172,100;255,172,100;251,173,100;244,173,100;237,173,100;231,172,100;224,171,100;216,170,100;206,167,100;198,164,100;188,158,100;179,154,100;168,145,100;162,139,100;153,130,100;147,121,100;145,114,100;143,106,100;143,102,100;147,93,100;373,256,100;373,250,100;377,238,100;382,230,100;388,224,100;395,220,100;399,219,100;406,219,100;414,221,100;425,228,100;431,234,100;436,245,100;439,251,100;439,258,100;439,265,100;436,272,100;432,283,100;424,290,100;414,296,100;409,297,100;402,297,100;392,294,100;384,288,100;378,279,100;375,272,100;374,265,100;373,262,100;219,287,100;227,291,100;230,294,100;232,297,100;235,300,100;236,304,100;236,308,100;236,314,100;234,317,100;231,322,100;228,326,100;224,329,100;221,329,100;215,335,100;207,338,100;195,341,100;187,342,100;185,341,100;177,340,100;173,339,100;170,337,100;169,334,100;167,331,100;167,327,100;167,324,100;170,319,100;172,314,100;177,308,100;186,299,100;193,293,100;200,289,100;204,287,100;207,286,100;211,286,100;
162,111,150;254,54,150;356,111,150;254,163,150;162,107,150;164,98,150;168,91,150;174,82,150;183,75,150;193,68,150;203,64,150;213,60,150;227,57,150;239,55,150;243,54,150;251,54,150;258,54,150;269,54,150;283,56,150;295,59,150;306,63,150;318,67,150;330,75,150;338,82,150;348,91,150;353,100,150;356,110,150;356,119,150;354,127,150;349,137,150;340,144,150;331,149,150;316,154,150;308,156,150;299,157,150;292,159,150;283,160,150;277,162,150;270,162,150;263,163,150;253,163,150;244,163,150;238,164,150;230,163,150;223,162,150;214,160,150;200,154,150;194,151,150;187,147,150;182,143,150;178,139,150;171,131,150;165,115,150;162,111,150;161,109,150;
178,112,200;254,65,200;337,111,200;254,155,200;177,105,200;181,95,200;185,90,200;191,84,200;195,83,200;200,79,200;208,74,200;219,70,200;227,67,200;233,66,200;240,65,200;250,65,200;260,65,200;273,65,200;280,66,200;290,69,200;305,75,200;314,79,200;322,84,200;330,94,200;334,100,200;337,109,200;338,114,200;338,117,200;336,124,200;329,133,200;318,140,200;306,146,200;293,150,200;288,151,200;272,154,200;266,155,200;246,155,200;237,155,200;230,154,200;218,150,200;208,147,200;198,141,200;190,136,200;184,129,200;179,118,200;178,111,200;177,109,200;
193,112,250;254,75,250;320,111,250;254,146,250;193,108,250;194,104,250;197,99,250;203,92,250;209,88,250;214,84,250;225,80,250;234,77,250;240,76,250;245,76,250;250,75,250;256,75,250;263,75,250;269,76,250;277,77,250;292,82,250;304,88,250;310,94,250;319,104,250;320,108,250;320,117,250;319,120,250;315,126,250;307,133,250;297,138,250;287,141,250;275,144,250;267,145,250;259,146,250;251,146,250;236,145,250;231,144,250;219,141,250;208,135,250;198,126,250;196,121,250;194,117,250;193,115,250;193,111,250;
211,112,300;254,86,300;300,111,300;254,137,300;211,111,300;214,104,300;219,98,300;227,94,300;236,89,300;244,87,300;250,86,300;257,86,300;263,86,300;268,87,300;281,91,300;291,98,300;297,102,300;299,108,300;300,112,300;298,117,300;293,125,300;269,135,300;262,136,300;256,137,300;216,122,300;212,117,300;211,113,300;294,124,300;289,128,300;285,130,300;280,132,300;268,136,300;264,136,300;249,137,300;245,136,300;240,136,300;235,134,300;232,134,300;229,132,300;225,130,300;221,127,300;217,124,300;215,121,300;212,118,300;211,114,300;
242,113,350;254,104,350;268,112,350;254,119,350;242,112,350;245,107,350;248,106,350;252,104,350;256,104,350;262,105,350;265,107,350;267,109,350;268,111,350;268,114,350;264,117,350;261,119,350;257,120,350;254,119,350;250,119,350;246,118,350;243,105,350;242,113,350;248,105,350];
x=A(:,1);y=A(:,2);z=A(:,3);
[X,Y,Z]=griddata(x,y,z,linspace(1,512)',linspace(1,512),'v4');%插值
n1=size(Y);
for i=1:n1(1,1)
    for j=1:n1(1,2)
        Y(i,j)=450-Y(i,j);
    end
end
n=size(Z);
for i=1:n(1,1)
    for j=1:n(1,2)
        if Z(i,j)<=0
            Z(i,j)=0;
        end
    end
end
figure('color',[1,1,1]),
surf(X,Y,Z)%三维曲面
xlabel('X');ylabel('Y');zlabel('Z')

%% 裁剪图形
x1 = 119.7; y1 = 371.6; z1 = 23.78;
x2 = 331.3; y2 = 98.01; z2 = 0;
nX = size(X);
m=1;
for i=1:nX(1,1)
    m=1;
    for j=1:nX(1,2)
        if X(i,j)>=x1&&X(i,j)<=x2   % 提取裁剪范围内的点
            X1(i,m) = X(i,j);
            Y1(i,m) = Y(i,j);
            Z1(i,m) = Z(i,j);
            m=m+1;
        end 
    end
end
X1 = X1(5:70,:);                    % 再次裁剪
Y1 = Y1(5:70,:);
Z1 = Z1(5:70,:);
figure('color',[1,1,1]),            % 设置图像背景为白色
surf(X1,Y1,Z1)                      % 三维曲面
xlabel('X');ylabel('Y');zlabel('Z')
hold on

%% 标记起点和终点
sta = [X1(1,27),Y1(18,1),Z1(18,27)];    %起点坐标
des = [X1(1,18),Y1(57,1),Z1(57,18)];    %终点坐标
plot3(X1(1,27),Y1(18,1),Z1(18,27),'r.','Markersize',40);%在图形上标点
plot3(X1(1,18),Y1(57,1),Z1(57,18),'r.','Markersize',40);

%% 寻找最优路径
% 将图形的行列转换为一行，每一个坐标对应一个点
sta = [253.9,340.6,353.2];  % 起点
sta = [X1(1,27),Y1(18,1),Z1(18,27)];  % 起点
des = [207.5,139.3,126.4];  % 终点
des = [X1(1,18),Y1(57,1),Z1(57,18)];  % 终点
nX1 = size(X1);
kk=1;
for i=1:nX1(1,1)
    for j=1:nX1(1,2)
        X2(1,kk) = X1(i,j);  % 化成点
        Y2(1,kk) = Y1(i,j);
        Z2(1,kk) = Z1(i,j);
        kk=kk+1;
    end
end
%% 求解每个图形点的距离值
for i=1:length(X2)
    for j=1:length(X2)
        Distance(i,j)=sqrt( (X2(i)-X2(j))^2 + (Y2(i)-Y2(j))^2 + (Z2(i)-Z2(j))^2 );
        Distance(j,i)=Distance(i,j);
    end
end
%% 求解邻接矩阵，相邻点之间置1，其余不相邻点置0
A=zeros(length(X2),length(X2)); % 构建邻接矩阵
% 第一行数据第一列到倒数第二列
for i = 1:nX1(1,2)-1
    A(i,i+1)=1;
    A(i,nX1(1,2)+i)=1;
    A(i,nX1(1,2)+i+1)=1; 
end
for i=2:nX1(1,1)-1 % 第二行到倒数第二行
    for j=2:nX1(1,2)-1 % 第二列到倒数第二列
        A( (i-1)*nX1(1,2)+j, (i-2)*nX1(1,2)+j ) = 1;    % 该点正上方点
        A( (i-1)*nX1(1,2)+j, (i-2)*nX1(1,2)+j-1 ) = 1;  % 该点正上方点，向左移一位
        A( (i-1)*nX1(1,2)+j, (i-2)*nX1(1,2)+j+1 ) = 1;  % 该点正上方点，向右移一位
        A( (i-1)*nX1(1,2)+j, (i-1)*nX1(1,2)+j-1 ) = 1;  % 该点行上，向左移一位
        A( (i-1)*nX1(1,2)+j, (i-1)*nX1(1,2)+j+1 ) = 1;  % 该点行上，向右移一位
        A( (i-1)*nX1(1,2)+j, (i)*nX1(1,2)+j ) = 1;      % 该点正下方点
        A( (i-1)*nX1(1,2)+j, (i)*nX1(1,2)+j-1 ) = 1;    % 该点正下方点，向左移一位
        A( (i-1)*nX1(1,2)+j, (i)*nX1(1,2)+j+1 ) = 1;    % 该点正下方点，向右移一位
    end
end
for i=1:length(X2)
    for j=1:length(X2)
        A(j,i)=A(i,j); %补全下半部分邻接矩阵
    end
end
%% 求最短路径
D=Distance.*A;          % 相连节点计算距离
D(find(D==0))=99999;    % 两点无边相连时赋值为inf
sta = [253.9,340.6,353.2];  % 起点
sta = [X1(1,27),Y1(18,1),Z1(18,27)];  % 起点
des = [207.5,139.3,126.4];  % 终点
des = [X1(1,18),Y1(57,1),Z1(57,18)];  % 终点
[Q_path, dmin] = dijkstra( 18*nX1(1,2)+27,57*nX1(1,2)+18 ,D);

%% 绘制最优路径数据点
figure('color',[1,1,1]),
surf(X,Y,Z)   % 三维曲面
xlabel('X');ylabel('Y');zlabel('Z')
hold on
plot3(X1(1,27),Y1(18,1),Z1(18,27),'r.','Markersize',40);
plot3(X1(1,18),Y1(57,1),Z1(57,18),'r.','Markersize',40);
for i=1:length(Q_path)
    row = ( Q_path(i) - mod(Q_path(i), nX1(1,2)) )/nX1(1,2);
    column = mod(Q_path(i),nX1(1,2));
    X3(i) = X1(row,column);
    Y3(i) = Y1(row,column);
    Z3(i) = Z1(row,column);
    plot3(X3(i),Y3(i),Z3(i),'r.','Markersize',40);
end