确定性时间序列分析方法

一、时间序列特点

　　时间序列数据的变化趋势有以下4种:

　　一个时间序列往往是以上几种变化趋势叠加或耦合形成的：

二、确定性时间序列分析

　　确定性时间序列分析方法将时间序列看做主要是由长期趋势、季节变动、循环变动和随机变动综合作用的结果。确定性数时间序列分析就是设法消除随机型波动，拟合确定性趋势。因而形成了长期趋势分析、季节变动分析、循环变动测得等一系列确定性时间序列分析方法。

（1）趋势性分析

（2）趋势性的提取方法

　　如果在预测时间范围以内，无突然变动且随机变动的方差σ2较小，并且过去和现在的演变趋势将继续发展到未来时，可用一些经验方法进行预测。主要方法有移动平均法、指数平滑法、趋势外推法，下面介绍具体方法。

三、移动平均法——提取长期趋势

3.1 概述　　

　　移动平均法是根据时间序列数据逐渐推移，依次计算包含一定项数的时序平均数，以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响，起伏较大，不易显示出发展趋势时，可用移动平均法，消除这些因素的影响，分析、预测序列的长期趋势。移动平均法有简单移动平均法（一次移动平均法），加权移动平均法，趋势移动平均法（二次移动平均法）等。

3.2 简单移动平均法（一次移动平均法）——基本趋势在某一水平上下波动

　　例子：

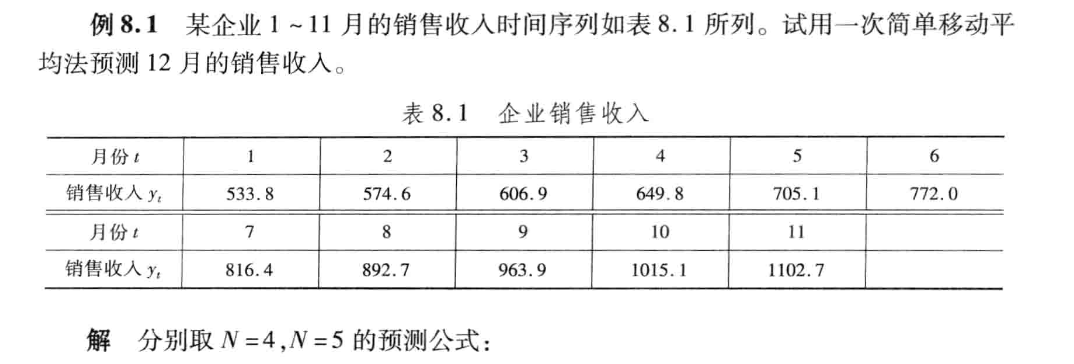
　　相关代码如下：

3.3 加权移动平均法

　　在简单移动平均公式中，每期数据在求平均时的作用是等同的。但是，每期数据所包含的信息量不一样，近期数据包含着更多关于未来情况的信心。因此，把各期数据等同看待是不尽合理的，应考虑各期数据的重要性，对近期数据给予较大的权重，这就是加权移动平均法的基本思想。

　　例子：

　　总结：在加权移动平均法中, 权重的选择同样具有一定的经验性。一般的原则是：近期数据的权数大，远期数据的权数小。至于大到什么程度和小到什么程度，则需要按照预测者对序列的了解和分析来确定。

3.4 趋势移动平均（二次移动平均法）——基本趋势与某一线性模型相吻合

　　简单移动平均法和加权移动平均法，在时间序列没有明显的趋势变动时，能够准确反映实际情况。但当时间序列出现直线增加或减少的变动趋势时，用简单移动平均法和加权移动平均法来预测就会出现滞后偏差。因此，需要进行修正，修正的方法是作二次移动平均，利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。

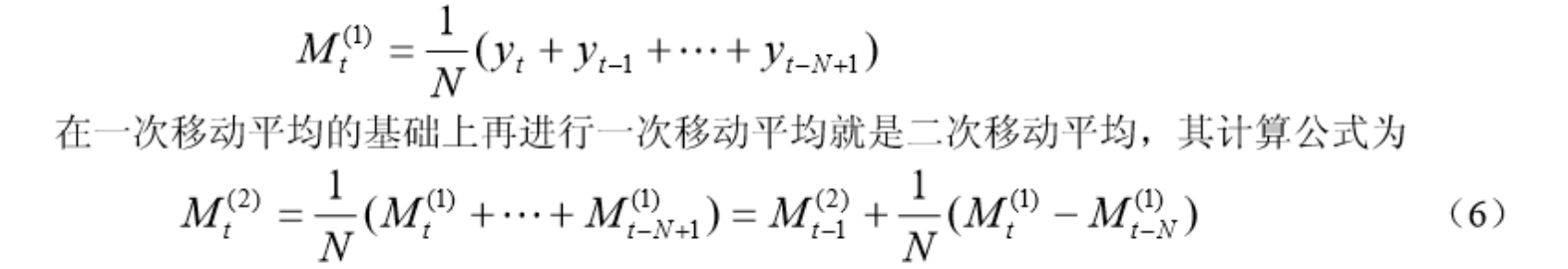
　　例子：

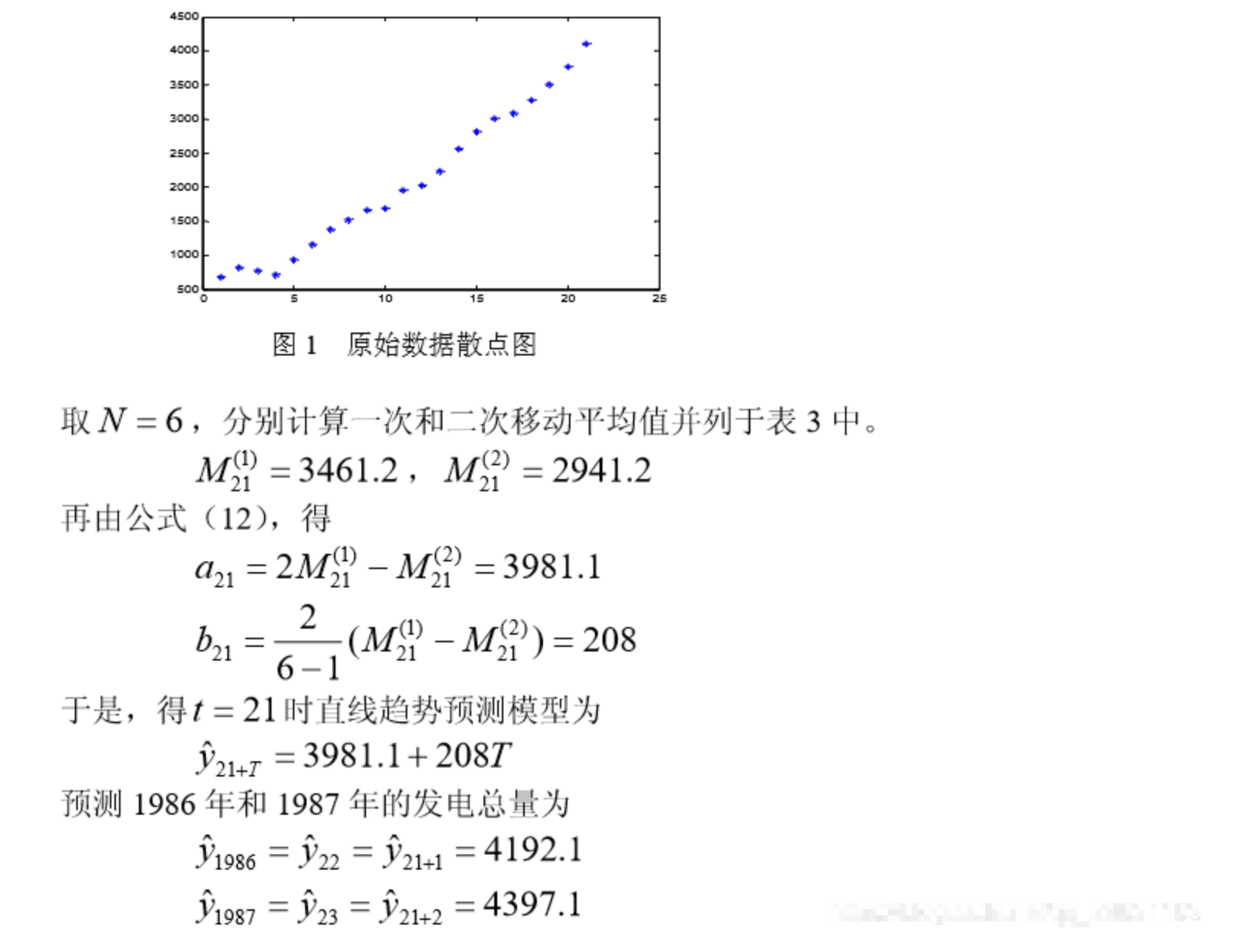
　　总结：趋势移动平均法对于同时存在直线趋势与周期波动的序列，是一种既能反映趋势变化，又可以有效地分离出来周期变动的方法。

2.5 移动平均法的不足

　　移动平均法只适合做近期预测，而且是预测目标的发展趋势变化不大的情况。如果目标的发展趋势存在其他的变化, 采用简单移动平均法就会产生较大的预测偏差和滞后。

　　一次移动平均实际上认为近 N 期数据对未来值影响相同，都加权1/N；而 N 期以前的数据对未来值没有影响，加权为 0。但是，二次及更高次移动平均数的权数却不是1/N，且次数越高，权数的结构越复杂，但永远保持对称的权数，即两端项权数小，中间项权数大，不符合一般系统的动态性。

四、指数平滑法——提取长期趋势

　　一般说来,历史数据对未来值的影响是随时间间隔的增长而递减的。所以,更切合实际的方法应是对各期观测值依时间顺序进行加权平均作为预测值。指数平滑法可满足这一要求,而且具有简单的递推形式。　　

　　指数平滑法根据平滑次数的不同,又分为一次指数平滑法、二次指数平滑法和三次指数平滑法等,下面分别介绍。

4.1 一次指数平滑法——基本趋势在某一水平上下波动

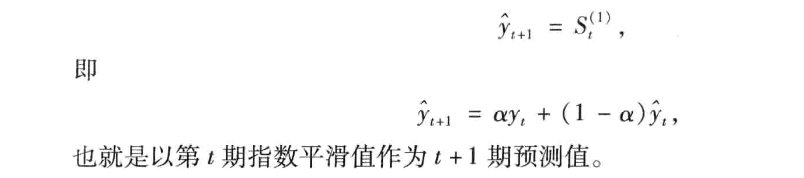
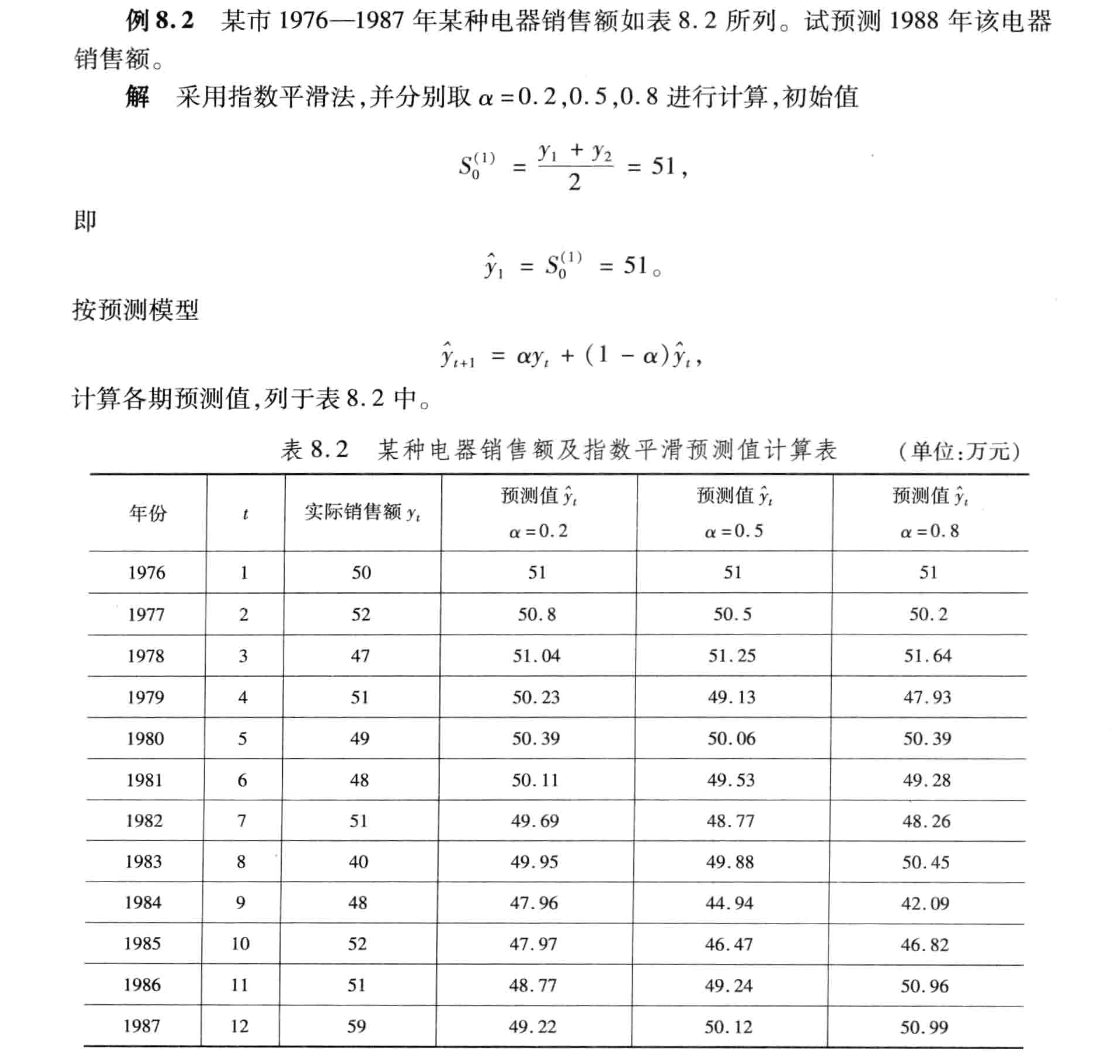
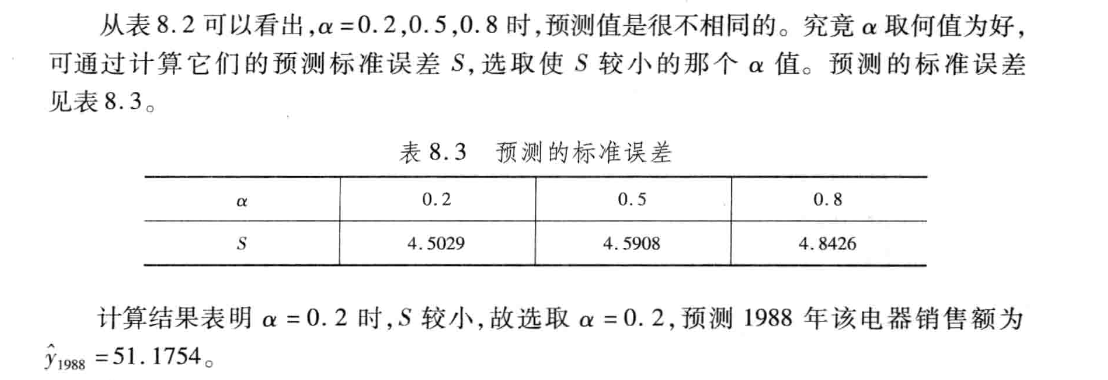
　　例子：

　　相关代码如下：

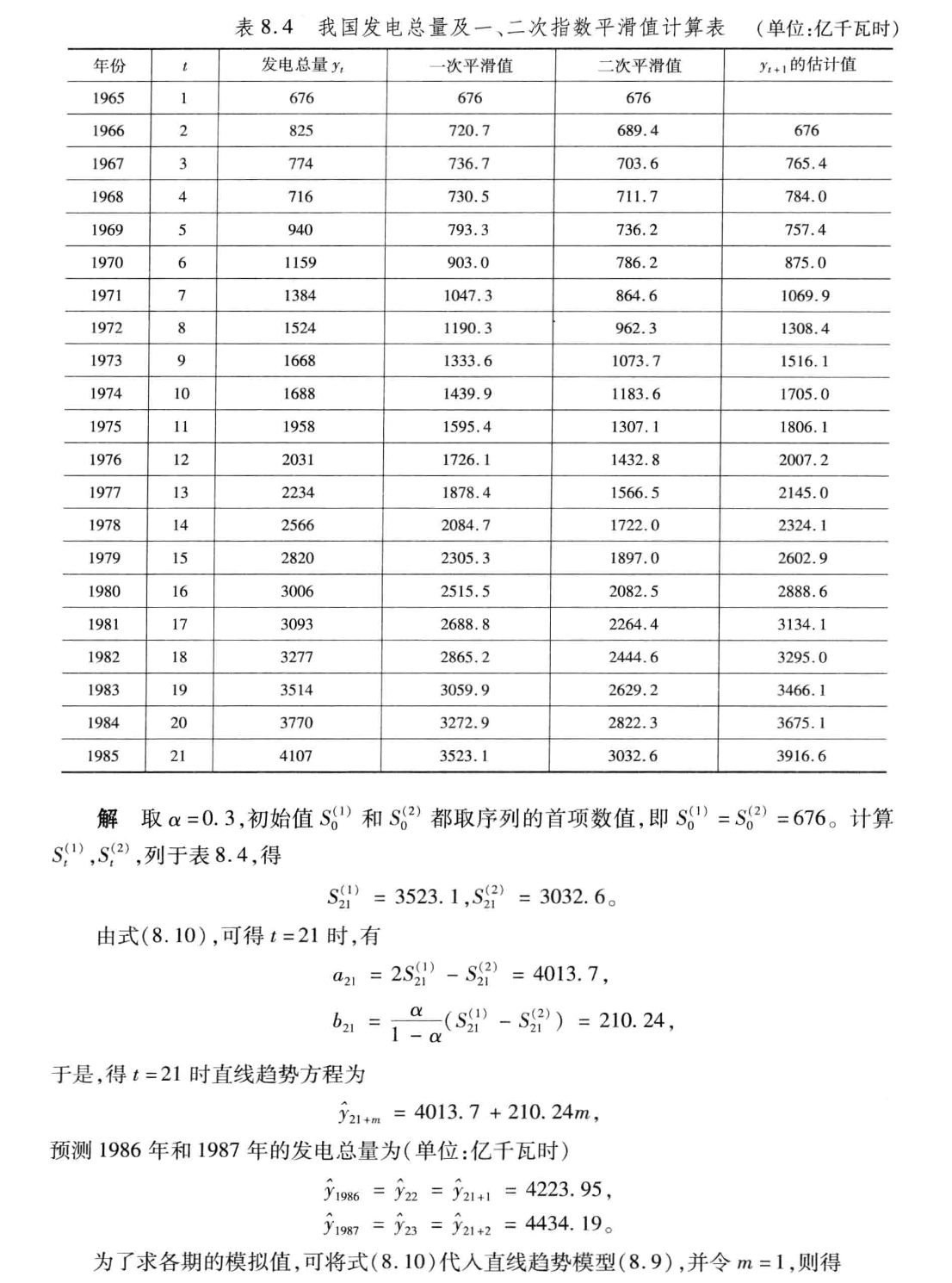
4.2 二次指数平滑法——基本趋势与某一线性模型相吻合

　　当时间序列的变动出现直线趋势时，适合用二次指数平滑法。

　　例子：

　　相关代码如下：

4.3 三次指数平滑法——基本趋势表现为二次曲线趋势

　　当时间序列出行二次趋势时，适合用三次指数平滑法。

　　例子：

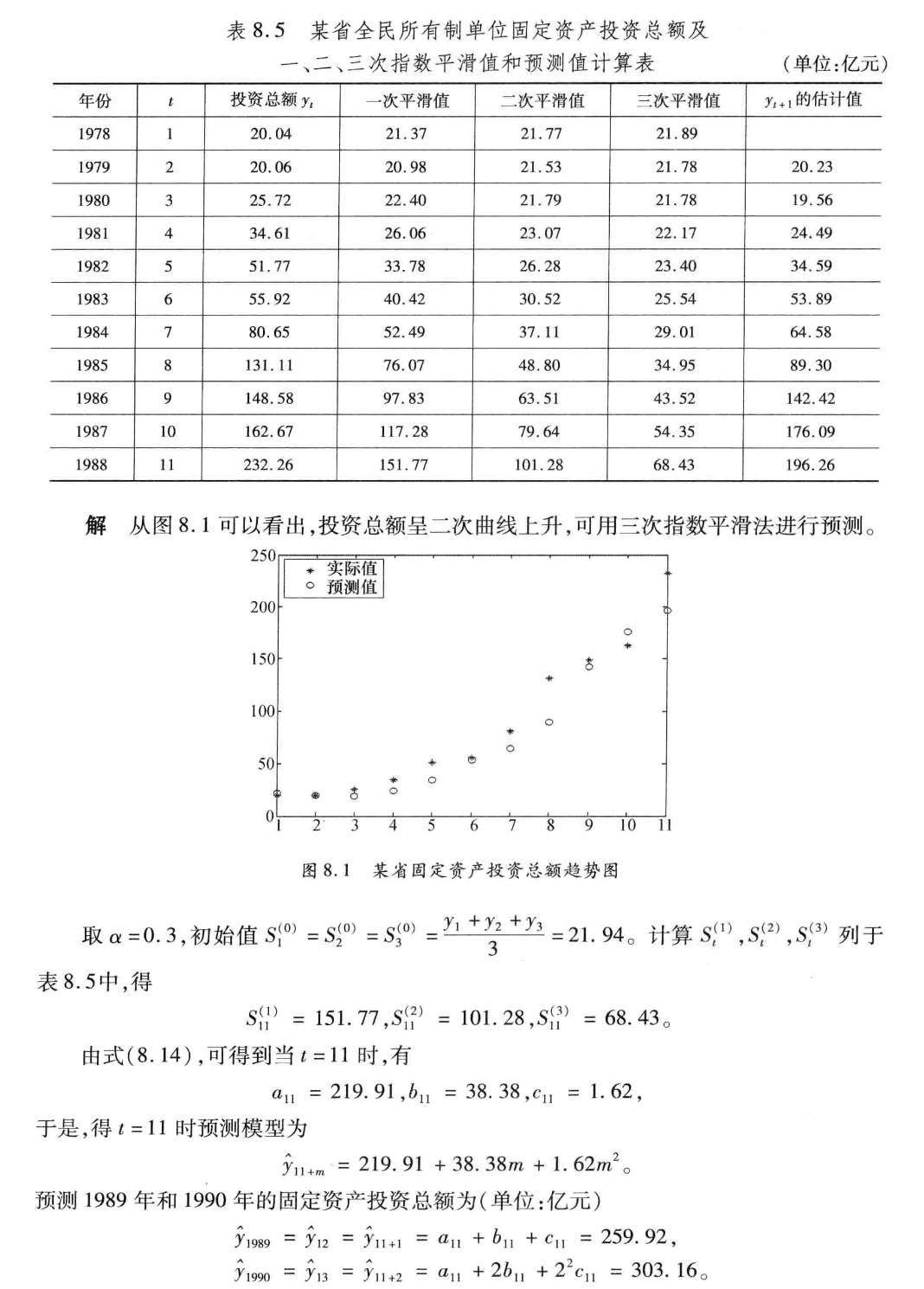
　　相关代码如下：

4.4 总结

五、差分指数平滑法——提取长期趋势

　　当时间序列的变动出现直线趋势，用一次指数平滑法会出现滞后偏差，其原因在于数据不满足模型要求。除了使用二次指数平滑法外，还可以从数据变换的角度来考虑改进措施，即在指数平滑前先对数据做一些技术上的处理，使之能适合于一次指数平滑模型，然后再对输出结果做技术上的返回处理，使之恢复为原变量的形态。

　　差分方法是改变数据变动趋势的简易方法。下面讨论如何用差分方法来进行指数平滑。

5.1 一阶差分指数平滑法——直线趋势

　　当时间序列呈直线增加时，可运用一阶差分指数平滑模型来预测。其公式如下：

即

　　指数平滑值实际上是一种加权平均数。因此,把序列中逐期增量的加权平均数( 指数平滑值)加上当前值的实际数进行预测，比一次指数平滑法只用变量以往取值的加权平均数作为下一期的预测更合理,从而使预测值始终围绕实际值上下波动，从根本上解决了在有直线增长趋势的情况下，用一次指数平滑法所得出的结果始终落后于实际值的问题。