城市居民食品分类及零售价格预测——聚类分析,灰色关联度分析以及时间序列预测模型
城市居民食品分类及零售价格预测










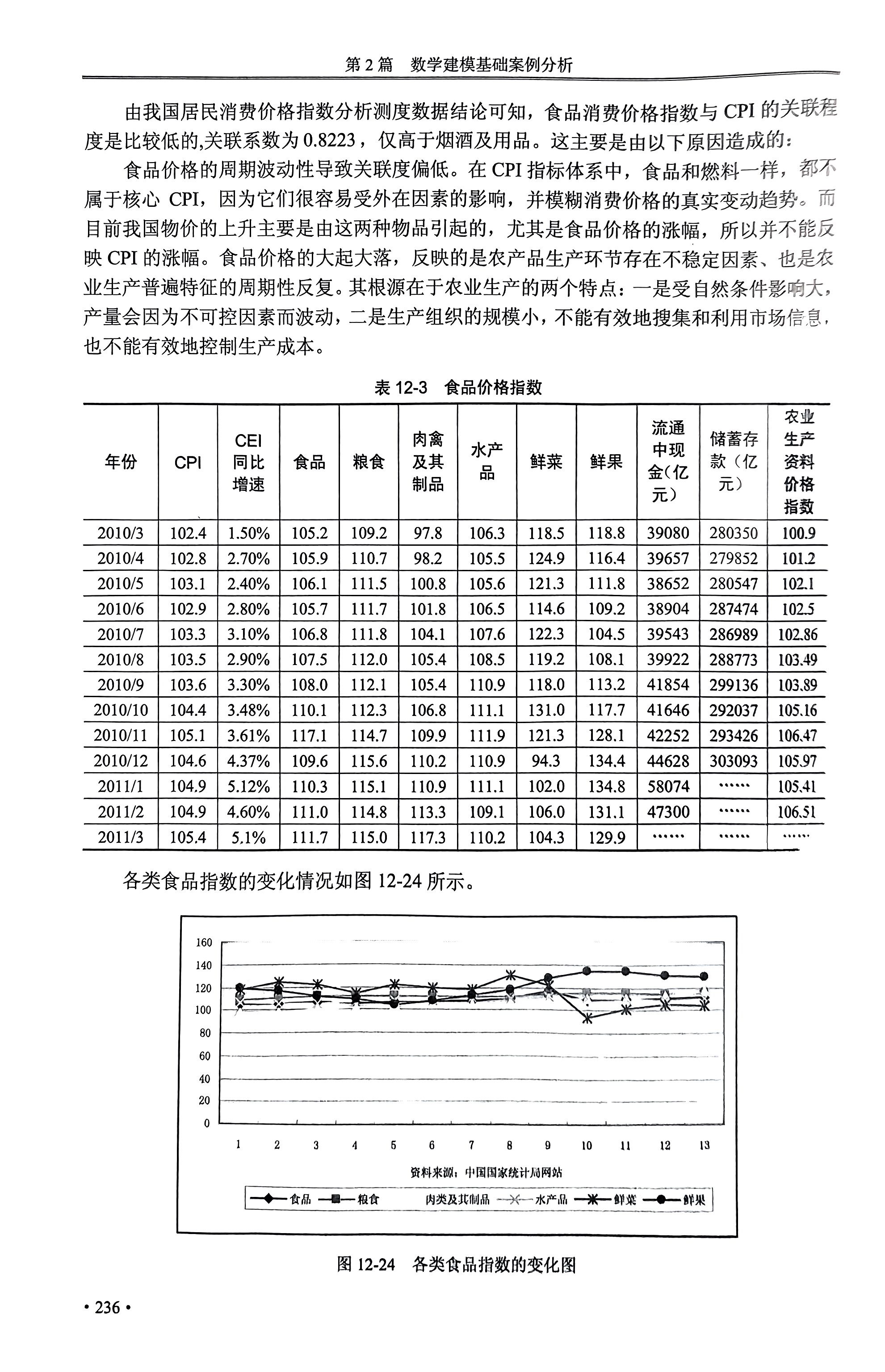






代码有问题,在后文修改




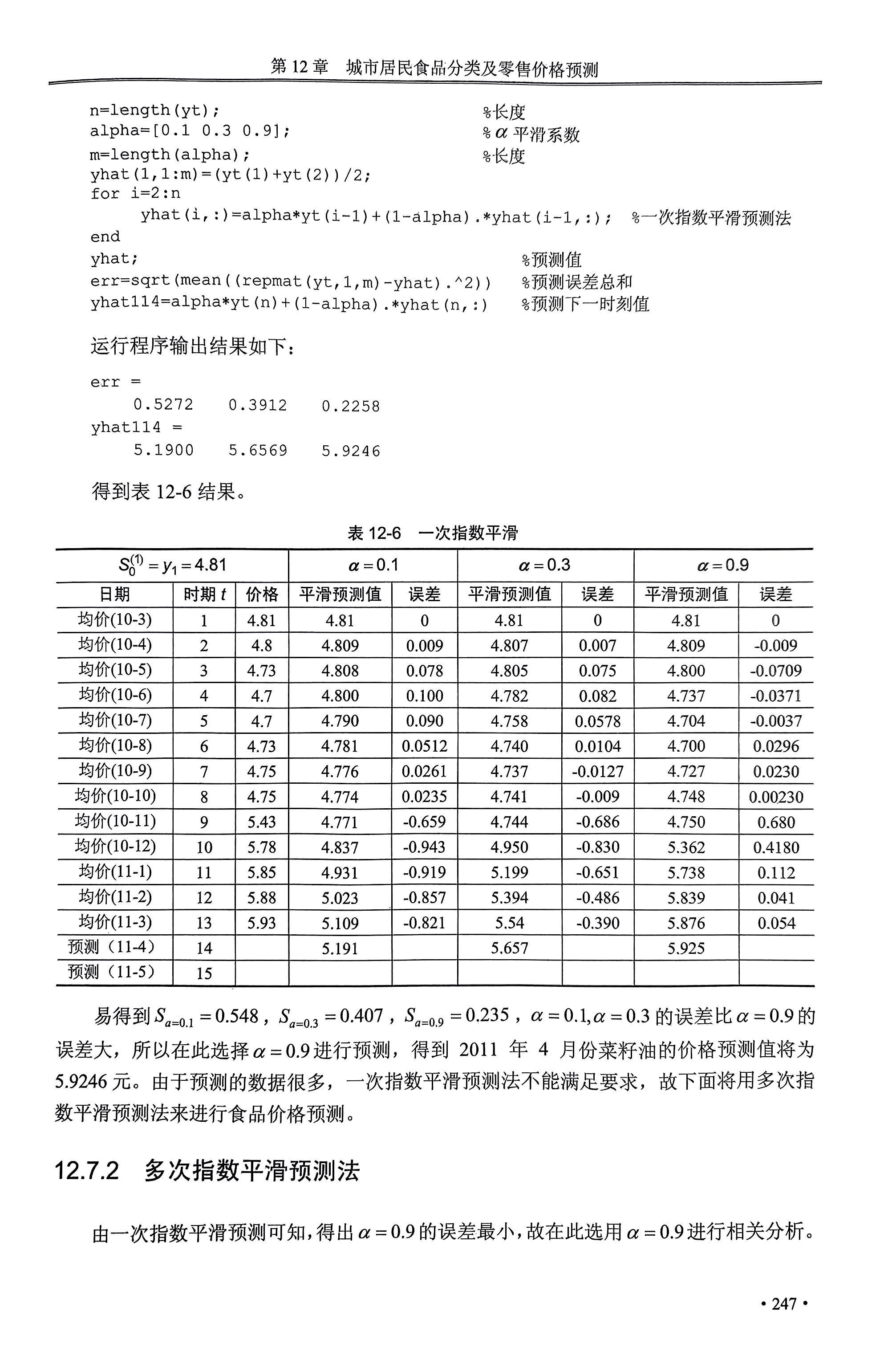

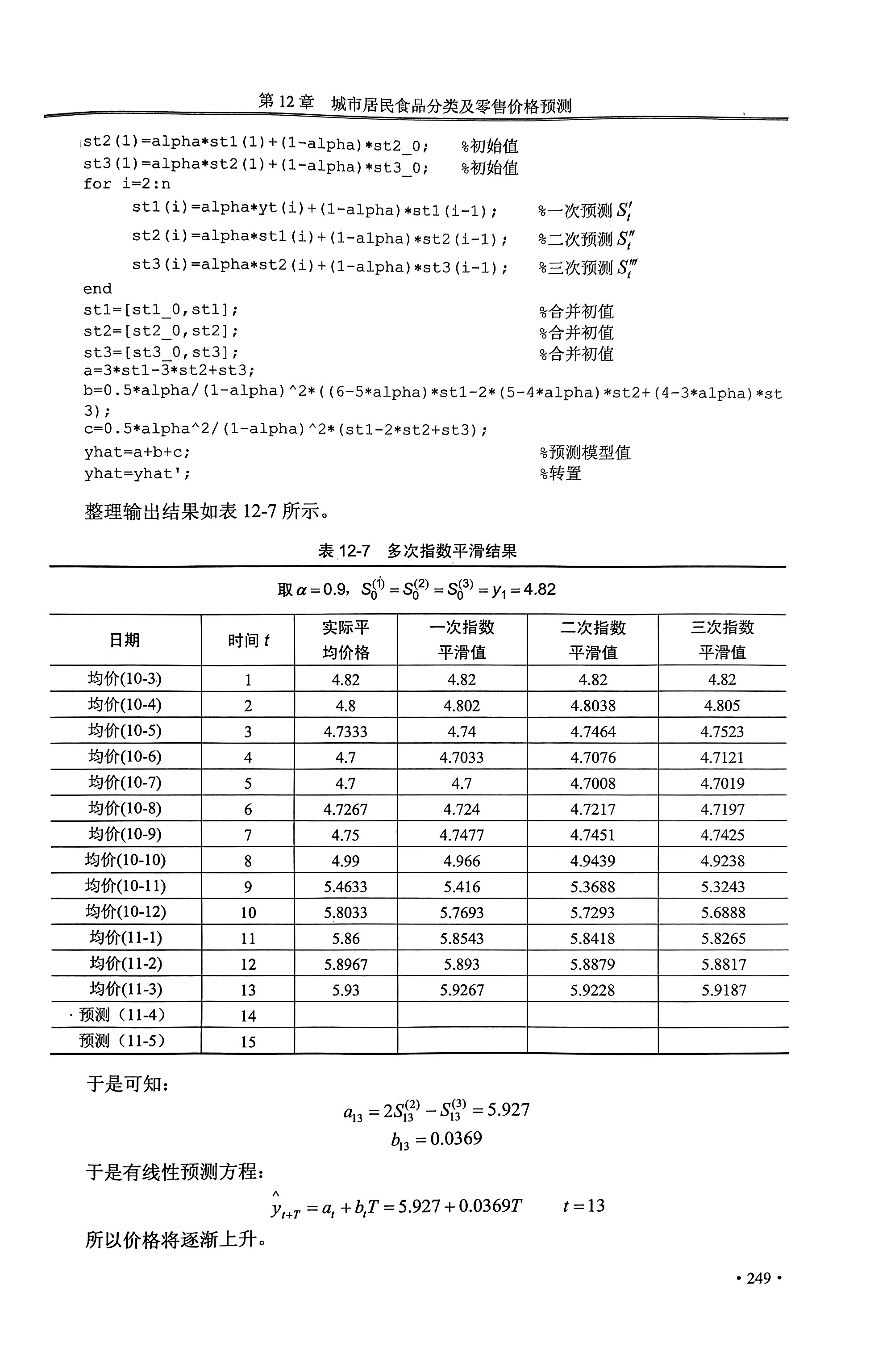



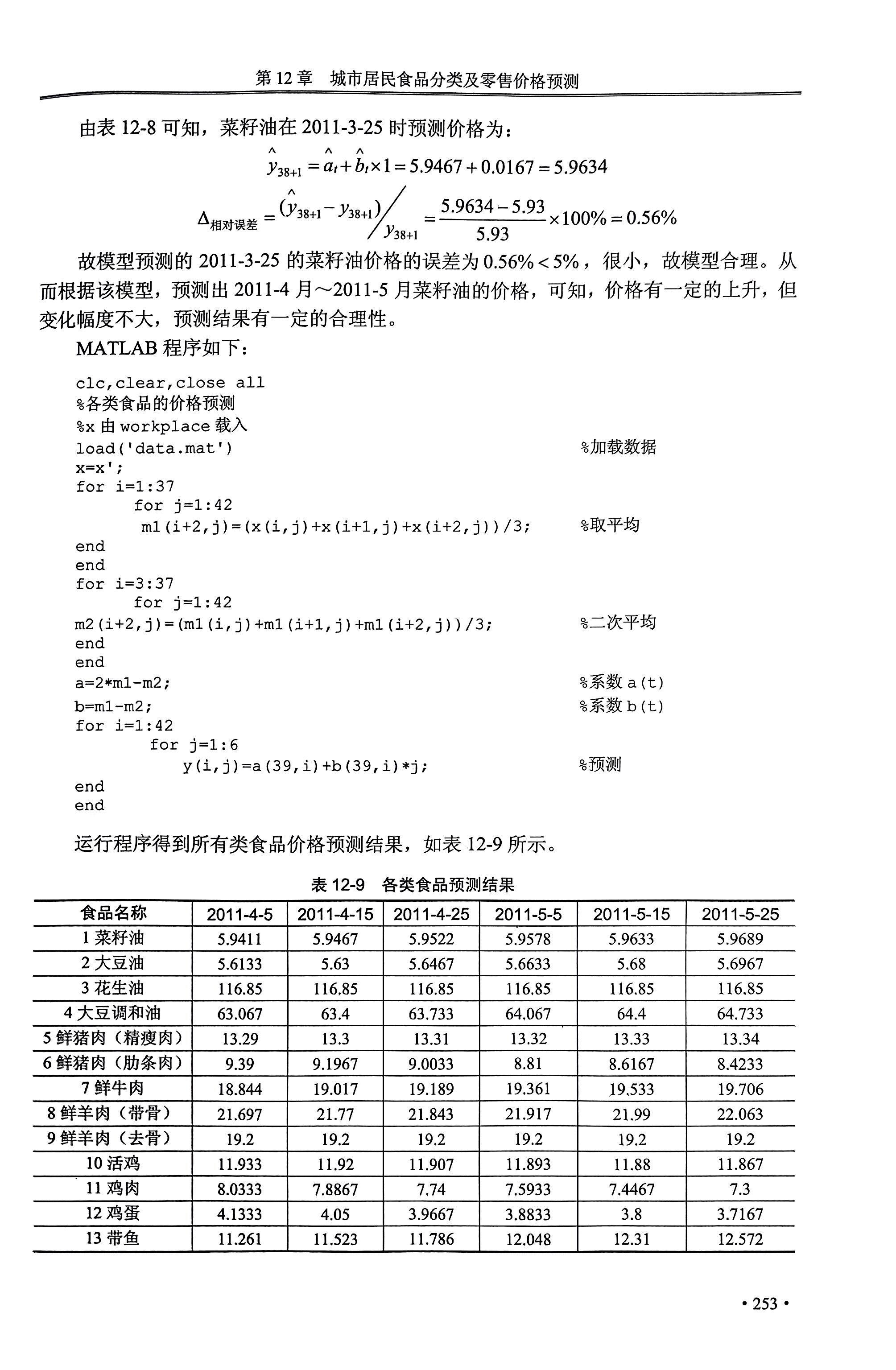
总结
一、价格特点描述
价格特点可从数值和增长率两个方面进行描述。
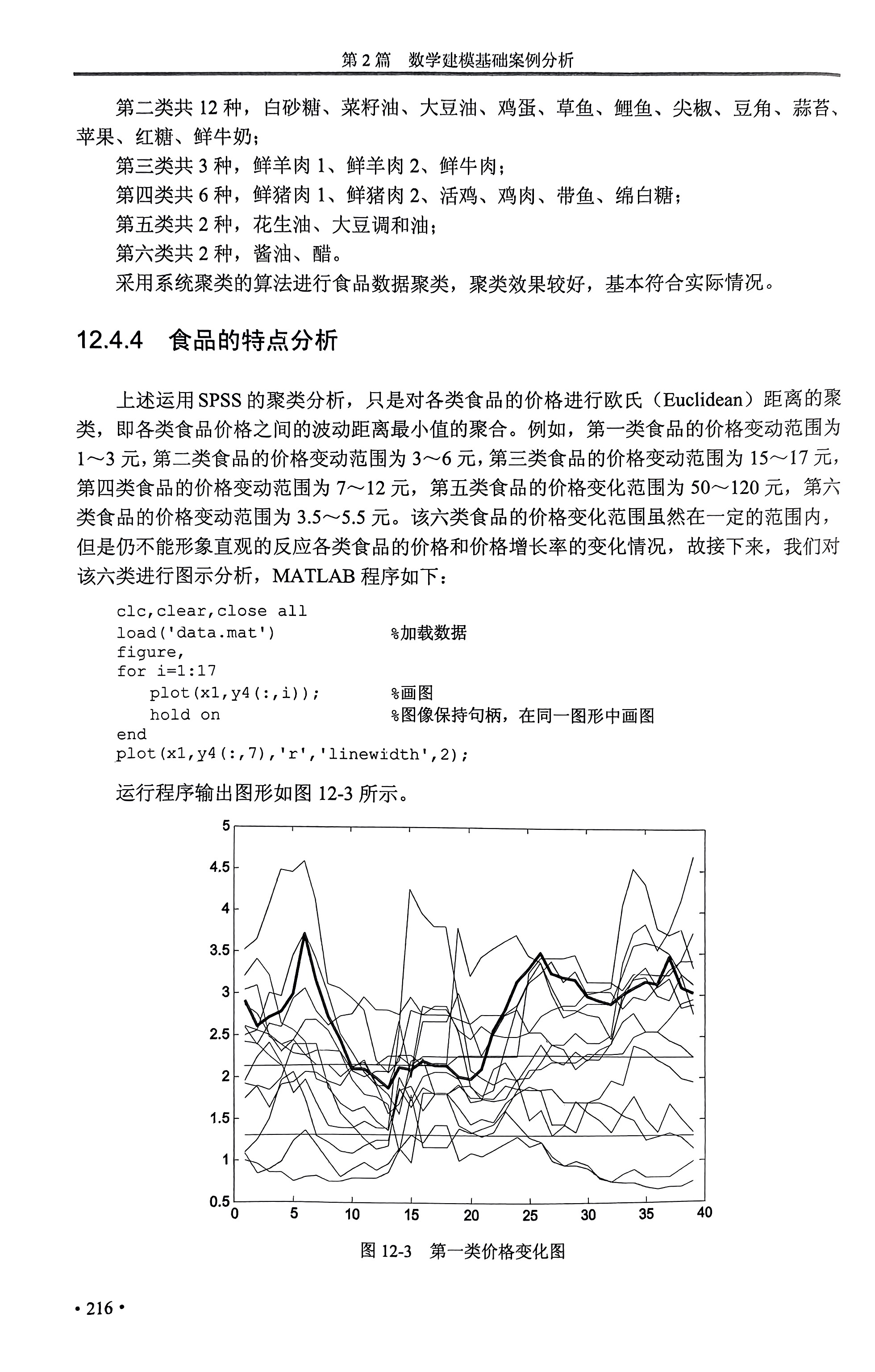
(1)数值描述法:直接用价格增长为描述对象,绘制价格——时间曲线。数值描述法可以直观地描述价格的变动趋势,但是由于各种食品的价格下相差较大且数据量很大,致使无法提现食品价格的变化的整体趋势。
总结价格数值的变化范围等。
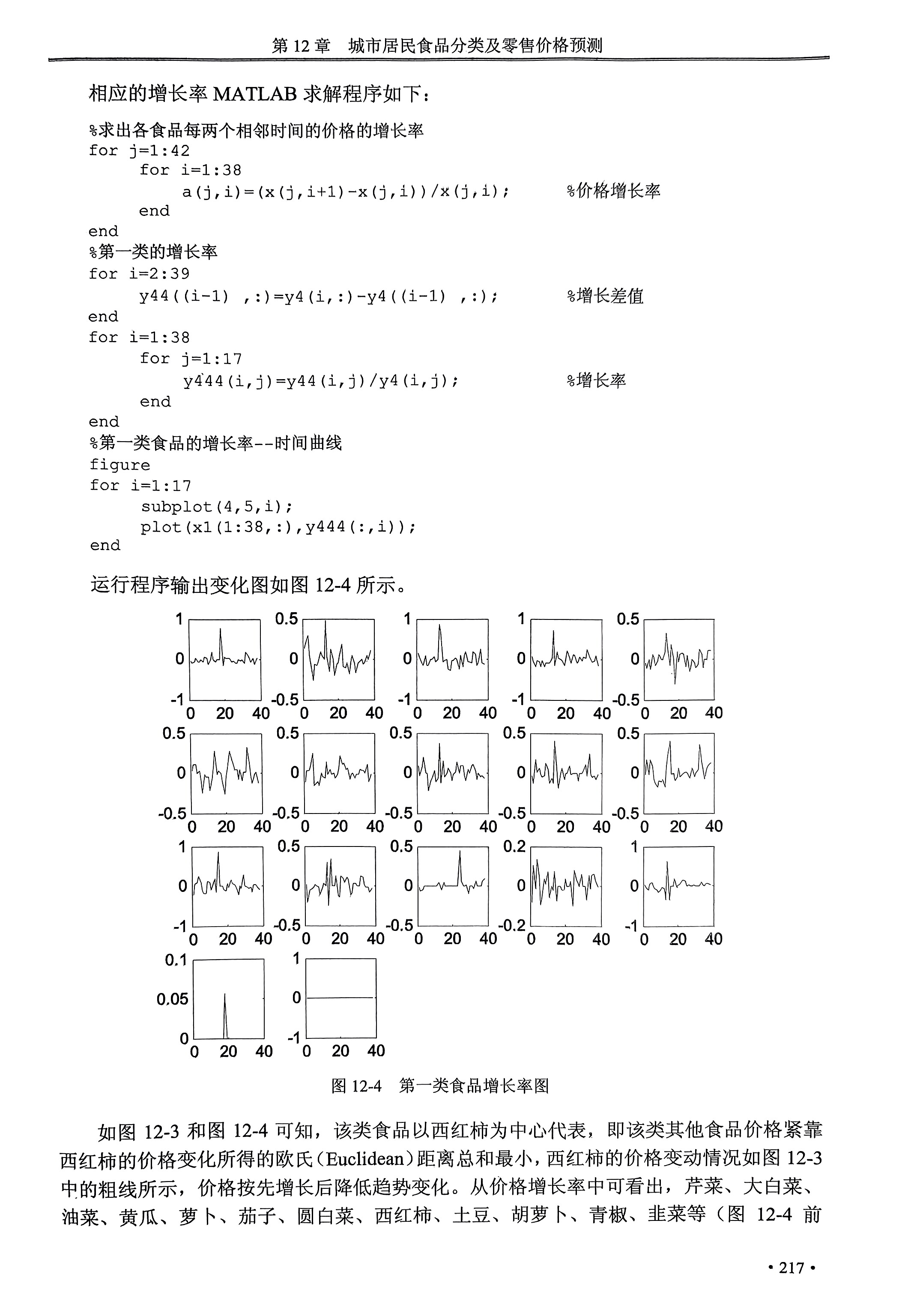
(2)增长率描述法:计算同种食品相邻时间点的价格增长率,绘制不同食品的增长率-时间曲线。增长率描述法依次计算相邻时期各食品价格的增长率,虽不能直接地反映价格值的变化,但可以直观地反映价格水平的变化。
总结增长率的变化区间,变化趋势(保持稳定或上涨或下降),持续时间,较大变化处等。在确定其变化幅度时,可设定一个标准,比如本题中将0.03和0.05设为变化幅度大小的评判标准。
二、聚类分析
聚类分析前需对数据进行处理:无量纲标准化
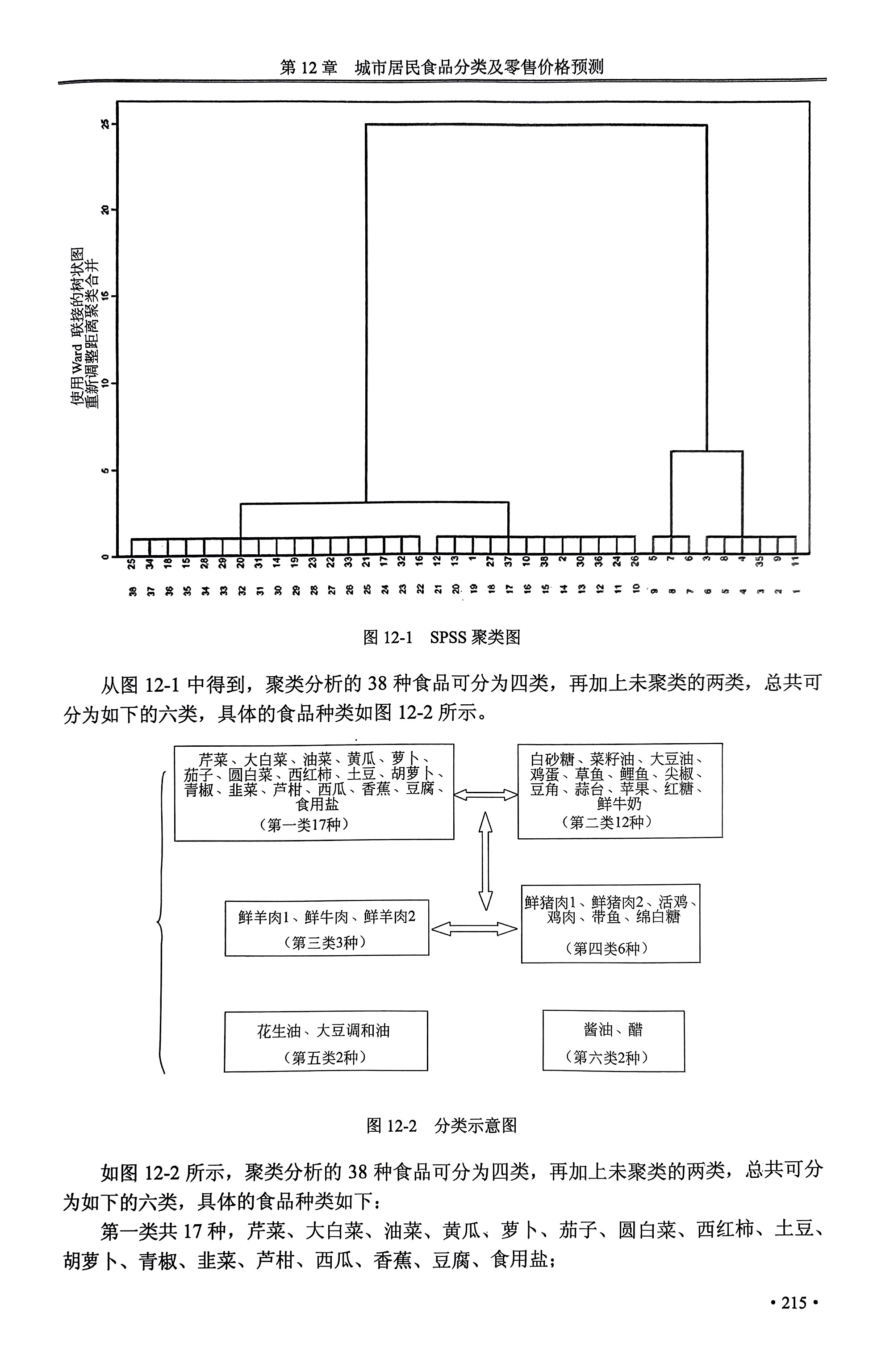
使用SPSS进行聚类分析。聚类结果中,每种类别都有一个聚类中心,以该聚类中心为代表比较其他食品价格值的变化及其增长率的变化。
三、灰色关联分析法
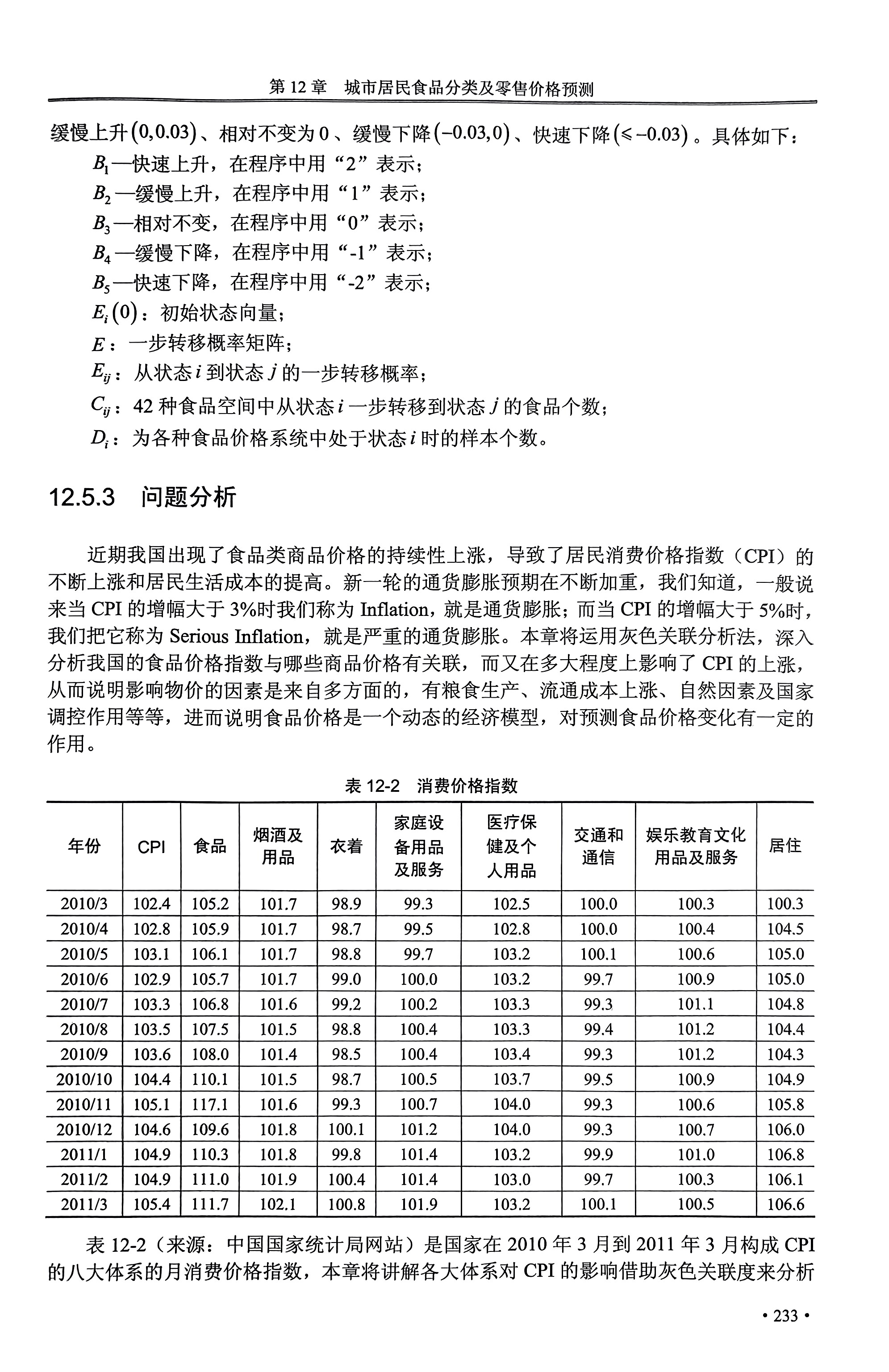
运用灰色关联分析法分析我国的食品价格指数与那些商品的价格有关,关联度有多大。
要分析两者之间的关系,先绘制两者的变化曲线进行比较,查看是否有关联度(变化趋势,变化幅度)
计算灰色关联度,相关代码如下
%%灰色关联度计算 clc,clear,close all %每一行为一个指标 y=[ 102.4 102.8 103.1 102.9 103.3 103.5 103.6 104.4 105.1 104.6 104.9 104.9 105.4 105.2 105.9 106.1 105.7 106.8 107.5 108 110.1 117.1 109.6 110.3 111 111.7 101.7 101.7 101.7 101.7 101.6 101.5 101.4 101.5 101.6 101.8 101.8 101.9 102.1 98.9 98.7 98.8 99 99.2 98.8 98.5 98.7 99.3 100.1 99.8 100.4 100.8 99.3 99.5 99.7 100 100.2 100.4 100.4 100.5 100.7 101.2 101.4 101.4 101.9 102.5 102.8 103.2 103.2 103.3 103.3 103.4 103.7 104 104 103.2 103 103.2 100 100 100.1 99.7 99.3 99.4 99.3 99.5 99.3 99.3 99.9 99.7 100.1 100.3 100.4 100.6 100.9 101.1 101.2 101.2 100.9 100.6 100.7 101 100.3 100.5 100.3 104.5 105 105 104.8 104.4 104.3 104.9 105.8 106 106.8 106.1 106.6]; y1=mean(y'); %求均值 y1=y1'; for i=1:9 for j=1:13 y2(i,j)=y(i,j)/y1(i); %初值像矩阵 end end for i=2:9 for j=1:13 y3(i-1,j)=abs(y2(i,j)-y2((i-1) ,j)); %差序列 end end a=1;b=0; %赋值是极大值和极小值 for i=1:8 for j=1:13 if(y3(i,j)<=a) a=y3(i,j); %计算minmin() elseif(y3(i,j)>=b) b=y3(i,j); %计算maxmax() end end end for i=1:8 for j=1:13 y4(i,j)=(a+0.5*b)/(y3(i,j)+0.5*b); %计算关联系数 end end y5=sum(y4')/12 %灰色关联度
四、马克立夫模型
为预测4和5月份的价格增长趋势的大致形式(快速上升、缓慢上升、相对不变、缓慢下降或快速下降),使用动态经济学模型中的马克立夫链。
数据预处理:将原始数据根据不同范围分类,在本题中快速上升(≥0.03),在程序中用“2”表示;缓慢上升(0,0.03),在程序中用“1”表示;相对不变0,在程序中用“0”表示;缓慢下降(-0.03,0),在程序中用“-1”表示;快速下降(≤-0.03),在程序中用“-2”表示;得到各类食品在不同时期的Bᵢ。
划分训练集和验证集:本文中总共有38组随时间变化的数据,将前37组作为训练集,第38组作为测试集。
马克立夫预测相关代码:
%% 马克立夫预测模型(概率预测) clc,clear,close all %% 加载数据 load('data.mat') %% 数据预处理(对数据进行分类) % 求增长率 for j=1:42 %42组样本 for i=1:38 %每组样本随时间变化有38组数据 a(j,i)=(x(j,i+1)-x(j,i))/x(j,i); end end % 分别为不同增长率赋值(分类) b=zeros(42,38); for j=1:42 for i=1:38 if a(j,i)>=0.03 b(j,i)=2; %2表示快速增长 elseif (a(j,i)<0.03)&&(a(j,i)>0) b(j,i)=1; %1表示缓慢增长 elseif a(j,i)==0 b(j,i)=0; %0表示相对稳定 elseif a(j,i)>-0.03 && a(j,i)<0 b(j,i)=-1; %-1表示缓慢下降 elseif a(j,i)<-0.03 b(j,i)=-2; %-2表示快速下降 end end end %% 统计25种变化的数量(初始5种状态,下一步可能有5种状态,总共可能有25种变化过程) c=zeros(42,25); for j=1:42 %42组样本 for i=1:36 %37组训练集,36组过程 if (b(j,i)==2&&b(j,i+1)==2) c(j,1)=c(j,1)+1; %从快速增长到快速增长过程数量 elseif(b(j,i)==2&&b(j,i+1)==1) c(j,2)=c(j,2)+1; %从快速增长到缓慢增长过程数量 elseif(b(j,i)==2&&b(j,i+1)==0) c(j,3)=c(j,3)+1; %从快速增长到相对稳定过程数量 elseif(b(j,i)==2&&b(j,i+1)==-1) c(j,4)=c(j,4)+1; %从快速增长到缓慢下降过程数量 elseif(b(j,i)==2&&b(j,i+1)==-2) c(j,5)=c(j,5)+1; %从快速增长到快速下降过程数量 elseif(b(j,i)==1&&b(j,i+1)==2) c(j,6)=c(j,6)+1; %从缓慢增长到快速增长过程数量 elseif(b(j,i)==1&&b(j,i+1)==1) c(j,7)=c(j,7)+1; %从缓慢增长到缓慢增长过程数量 elseif(b(j,i)==1&&b(j,i+1)==0) c(j,8)=c(j,8)+1; %从缓慢增长到相对稳定过程数量 elseif(b(j,i)==1&&b(j,i+1)==-1) c(j,9)=c(j,9)+1; %从缓慢增长到缓慢下降过程数量 elseif(b(j,i)==1&&b(j,i+1)==-2) c(j,10)=c(j,10)+1; %从缓慢增长到快速下降过程数量 elseif(b(j,i)==0&&b(j,i+1)==2) c(j,11)=c(j,11)+1; %从相对稳定到快速增长过程数量 elseif(b(j,i)==0&&b(j,i+1)==1) c(j,12)=c(j,12)+1; %从相对稳定到缓慢增长过程数量 elseif(b(j,i)==0&&b(j,i+1)==0) c(j,13)=c(j,13)+1; %从相对稳定到相对稳定过程数量 elseif(b(j,i)==0&&b(j,i+1)==-1) c(j,14)=c(j,14)+1; %从相对稳定到缓慢下降过程数量 elseif(b(j,i)==0&&b(j,i+1)==-2) c(j,15)=c(j,15)+1; %从相对稳定到快速下降过程数量 elseif(b(j,i)==-1&&b(j,i+1)==2) c(j,16)=c(j,16)+1; %从缓慢下降到快速增长过程数量 elseif(b(j,i)==-1&&b(j,i+1)==1) c(j,17)=c(j,17)+1; %从缓慢下降到缓慢增长过程数量 elseif(b(j,i)==-1&&b(j,i+1)==0) c(j,18)=c(j,18)+1; %从缓慢下降到相对稳定过程数量 elseif(b(j,i)==-1&&b(j,i+1)==-1) c(j,19)=c(j,19)+1; %从缓慢下降到缓慢下降过程数量 elseif(b(j,i)==-1&&b(j,i+1)==-2) c(j,20)=c(j,20)+1; %从缓慢下降到快速下降过程数量 elseif(b(j,i)==-2&&b(j,i+1)==2) c(j,21)=c(j,21)+1; %从快速下降到快速增长过程数量 elseif(b(j,i)==-2&&b(j,i+1)==1) c(j,22)=c(j,22)+1; %从缓慢下降到缓慢增长过程数量 elseif(b(j,i)==-2&&b(j,i+1)==0) c(j,23)=c(j,23)+1; %从缓慢下降到相对稳定过程数量 elseif(b(j,i)==-2&&b(j,i+1)==-1) c(j,24)=c(j,24)+1; %从缓慢下降到缓慢下降过程数量 elseif(b(j,i)==-2&&b(j,i+1)==-2) c(j,25)=c(j,25)+1; %从缓慢下降到快速下降过程数量 end end end d=zeros(42,5); % 累加求和 for i=1:42 for j=1:25 if(j<6) d(i,1)=d(i,1)+c(i,j); %初始状态为快速上升数量 elseif(j>5&&j<11) d(i,2)=d(i,2)+c(i,j); %初始状态为缓慢上升数量 elseif(j>10&&j<16) d(i,3)=d(i,3)+c(i,j); %初始状态为相对稳定数量 elseif(j>15&&j<21) d(i,4)=d(i,4)+c(i,j); %初始状态为缓慢下降数量 else d(i,5)=d(i,5)+c(i,j); %初始状态为快速下降数量 end end end %% 一步转移概率矩阵; f=b(:,37); %37组训练集中最后1组数据,用于预测之后的状态 e= zeros(5,5); %计算每种变化的概率,即一步转移概率矩阵e。 %计算方式,在同一初始状态下,转换成其他状态的概率,即Dij/Di for i=1:42 %42组样本 for j=1:25 if(j<6) if(d(i,1)==0) e(1,j)=0; else e(1,j)=c(i,j)/d(i,1); end elseif(j>5&&j<11) if(d(i,2)==0) e(2,j-5)=0; else e(2,j-5)=c(i,j)/d(i,2); end elseif(j>10&&j<16) if(d(i,3)==0) e(3,j-10)=0; else e(3,j-10)=c(i,j)/d(i,3); end elseif(j>15&&j<21) if(d(i,4)==0) e(4,j-15)=0; else e(4,j-15)=c(i,j)/d(i,4); end else if(d(i,5)==0) e(5,j-20)=0; else e(5,j-20)=c(i,j)/d(i,5); end end end %预测4、5月的增长率 g=zeros(i,5); if(f(i,1)==2) %初始状态为快速增长 h=[1 0 0 0 0 ]*e %预测第38组数据 for k=1:6 h=h*e %预测4、5月的数据 end elseif(f(i,1)==1) g(i,:)=[0 1 0 0 0 ]; h=g(i,:)*e %预测第38组数据 for k=1:6 h=h*e %预测4、5月的数据 end elseif(f(i,1)==0) g(i,:)=[0 0 1 0 0 ]; h=g(i,:)*e %预测第38组数据 for k=1:6 h=h*e %预测4、5月的数据 end elseif(f(i,1)==-1) g(i,:)=[0 0 0 1 0 ]; h=g(i,:)*e %预测第38组数据 for k=1:6 h=h*e %预测4、5月的数据 end elseif(f(i,1)==-2) g(i,:)=[0 0 0 0 1 ]; h=g(i,:)*e %预测第38组数据 for k=1:6 h=h*e %预测4、5月的数据 end end end
得到的结果为下一步转变为5种不同状态的概率,按最大概率原则,选择其中最大者对应的状态为预测结果。
五、时间序列指数平滑预测法
马尔科夫链模型只能预测食品价格的大致增长情况,不能直接得到对应的价格数值。为了进一下得到更直观的反应物价的变化情况,本文使用了时间序列指数预测法。
1、一次指数预测法


预测的标准误差为:
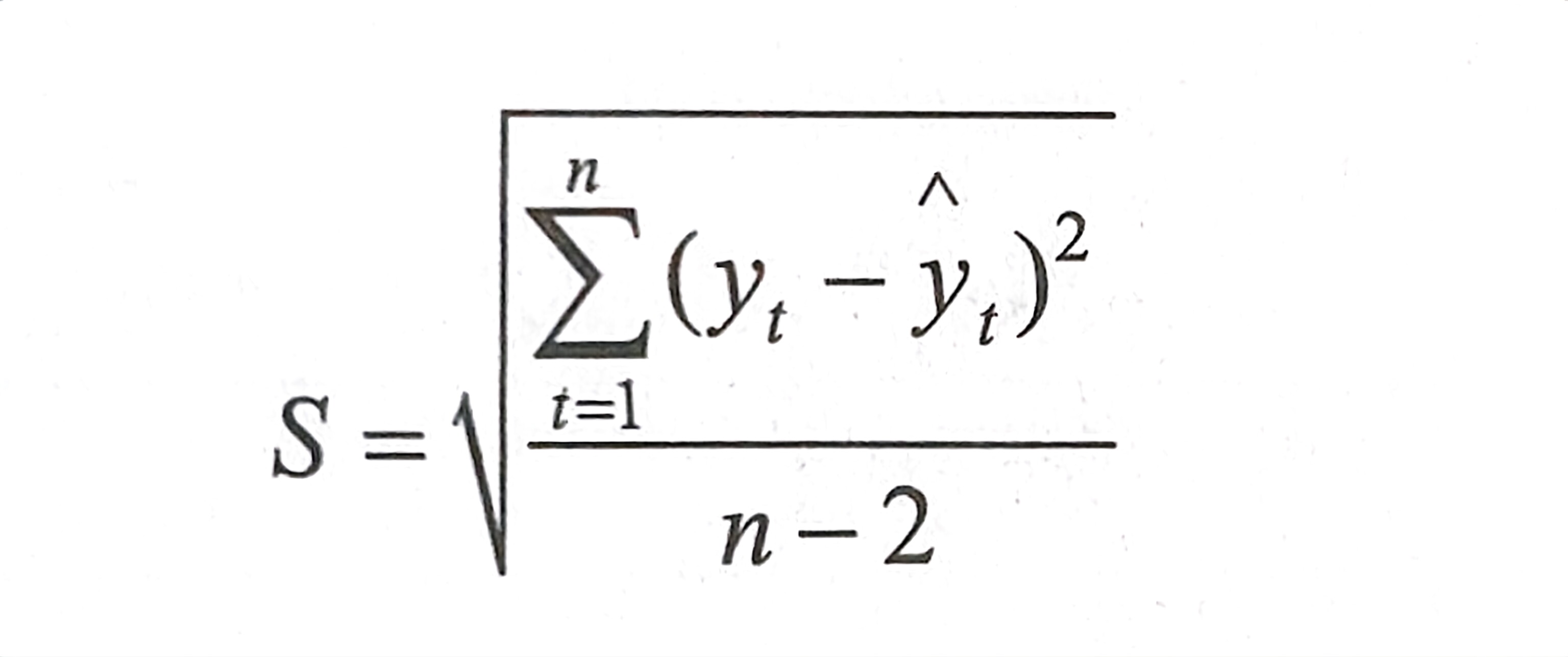
相关代码为:
%一次指数平滑预测 clc,clear %导入时间序列数据 yx =[4.81;4.8;4.73;4.7;4.7;4.73;4.75;4.75;5.43;5.78;5.85;5.88;5.93]; yt=yx; %yt n=length(yt); %长度 alpha=[0.1 0.3 0.9];%alpha平滑系数,可选取多个进行比较 m=length(alpha); yhat(1,1:m)=(yt(1)+yt(2))/2;%yhat初始值 for i=2:n yhat(i,:)=alpha*yt(i-1)+(1-alpha).*yhat(i-1,:);%一次指数平滑预测法 end yhat; % 预测值 err=sqrt(mean((repmat(yt,1,m)-yhat).^2)) % 预测误差总和 yhat114=alpha*yt(n)+(1-alpha).*yhat(n,:) % 预测下一时刻值
通过比较不同a平滑系数下的误差,选择使用误差最小的a平滑系数以及其对应的预测值。
2、多次指数平滑预测
当时间序列的变动出现直线趋势时,则需要使用二次指数平滑法,其计算公式为:

相应代码为:
%二次指数平滑法 clc,clear %导入时间序列数据 yx =[4.81;4.8;4.73;4.7;4.7;4.73;4.75;4.75;5.43;5.78;5.85;5.88;5.93]; yt=yx; %yt n=length(yt);%时间序列长度 alpha=0.9; %alpha平滑系数 st1(1)=yt(1); %初始值S1(0)=y1 st2(1)=yt(1); %初始值S2(0)=y1 for i=2:n st1(i)=alpha*yt(i)+(1-alpha)*st1(i-1); %一次预测S1 st2(i)=alpha*st1(i)+(1-alpha)*st2(i-1); %二次预测S2 end a=2*st1-st2; %计算系数a b=alpha/(1-alpha)*(st1-st2); %计算系数b yhat=a+b; %得到直线趋势方程(一步预测,m=1) yhat=yhat' str=char(['C',int2str(n+2)]); %字符型输出
3、三次指数平滑法
当时间序列的变化表现为二次曲线趋势时,则需要使用三次指数平滑法,其计算公式为:

相关代码为:
%% 三次指数平滑法 clc,clear %导入数据 yx =[4.81;4.8;4.73;4.7;4.7;4.73;4.75;4.75;5.43;5.78;5.85;5.88;5.93]; yt=yx;%yt n=length(yt);%时间序列长度 alpha=0.9; %alpha平滑系数 st1_0=mean(yt(1:3)); %初始值S1(0)=(y1+y2+y3)/3 st2_0=st1_0; %初始值S2(0)=(y1+y2+y3)/3 st3_0=st1_0; %初始值S3(0)=(y1+y2+y3)/3 st1(1)=alpha*yt(1)+(1-alpha)*st1_0; %初始值S1(1) st2(1)=alpha*st1(1)+(1-alpha)*st2_0;%初始值S2(1) st3(1)=alpha*st2(1)+(1-alpha)*st3_0;%初始值S3(1) for i=2:n st1(i)=alpha*yt(i)+(1-alpha)*st1(i-1); %一次预测 st2(i)=alpha*st1(i)+(1-alpha)*st2(i-1); %二次预测 st3(i)=alpha*st2(i)+(1-alpha)*st3(i-1); %三次预测 end st1=[st1_0,st1]; %合并初值 st2=[st2_0,st2]; %合并初值 st3=[st3_0,st3]; %合并初值 a=3*st1-3*st2+st3; %系数a b=0.5*alpha/(1-alpha)^2*((6-5*alpha)*st1-2*(5-4*alpha)*st2+(4-3*alpha)*st3);%系数b c=0.5*alpha^2/(1-alpha)^2*(st1-2*st2+st3);%系数c yhat=a+b+c;%二次曲线趋势方程(单步预测,m=1) yhat=yhat';
六、时间序列移动平均预测法
1、简单的一次移动平均法
当预测目标的基本趋势在某一水平上下波动时,可用一次移动平均法建立预测模型:
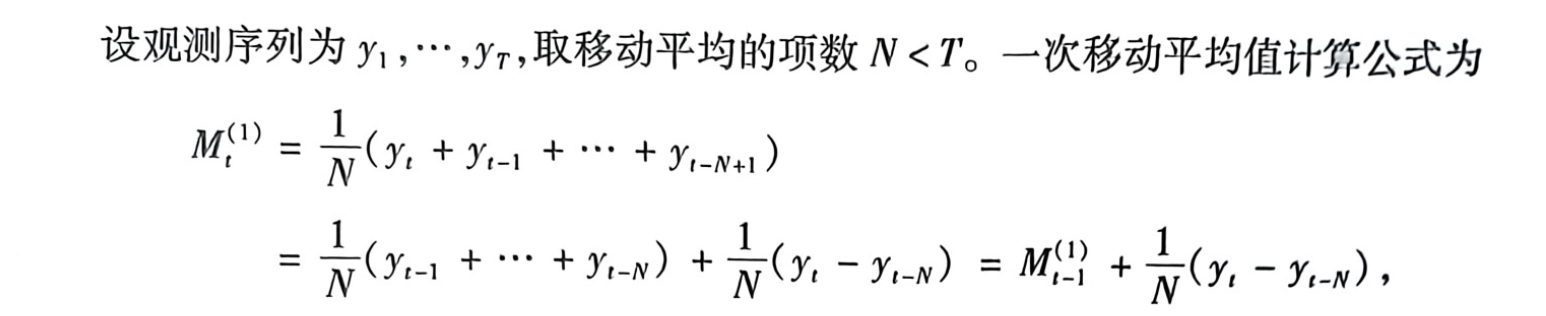
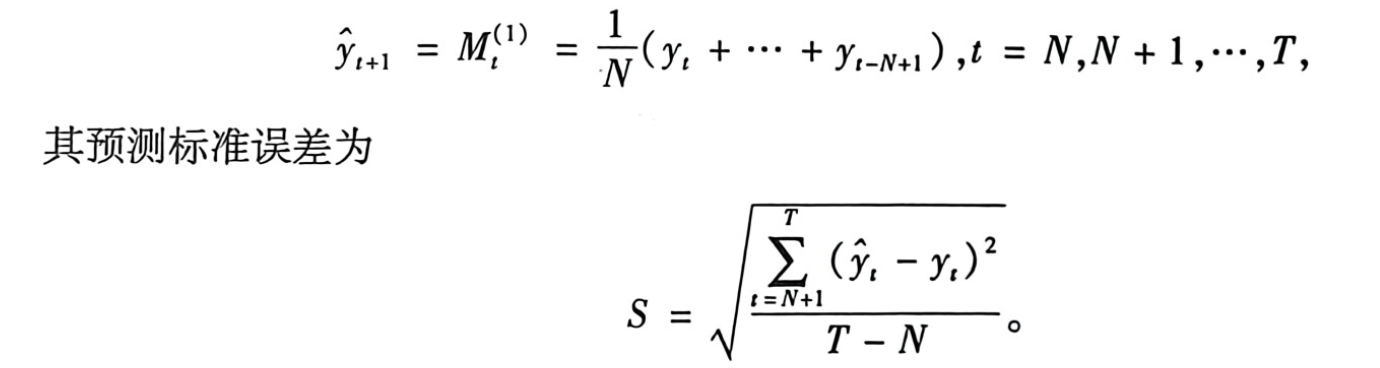

2、线性二次移动平均法
当预测目标的基本趋势与某一线性模型相吻合时,常使用二次移动平均法:

但序列同时存在线性趋势与周期波动时,可用趋势移动平均法建立预测模型:
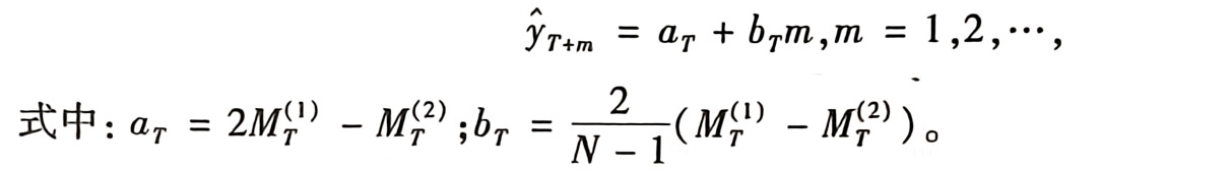
相关代码:
%移动平均法 clc,clear,close all %导入数据 x1=[4.83 4.83 4.8 4.8 4.8 4.8 4.8 4.7 4.7 4.7 4.7 4.7 4.7 4.7 4.7 4.7 4.74 4.74 4.75 4.75 4.75 4.75 4.92 5.3 5.43 5.48 5.48 5.78 5.78 5.85 5.85 5.85 5.88 5.88 5.88 5.93 5.93 5.93 5.93]; x1=x1'; for i=1:37 m1(i+2)=(x1(i)+x1(i+1)+x1(i+2))/3;%一次移动平均值,N=3 end for i=3:37 m2(i+2)=(m1(i)+m1(i+1)+m1(i+2))/3;%二次移动平均值,N=3 end m1=m1'; m2=m2'; a=2*m1-m2;%系数a(t) b=m1-m2;%系数b(t) for i=1:6 y(:,i)=a(39,1)+b(39,1)*i;%y=a+bm,预测之后6组数据 end y





