日报销售问题——最优化灵敏度分析

日报销售问题

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

总结

一、求解函数最优化解

　　先根据题意建立数学模型，即通过机理构建函数方程，带入数值，进行绘图。

　　求解最大最小值问题时,可根据函数的性质（定性分析）和函数求导等于0（定量分析）找到最佳解。

%%绘制函数图像
clc,clear,close all
p=1.5:0.001:1.70;  %确定自变量范围
Q=-50000*p.^2+155000*p-120000;  %方程
max(Q)  %最大值
plot(p,Q)   %绘图
hold on
plot([1.5,1.7],[0,0])   %画0X轴
xlabel('p') %坐标标记
ylabel('Q')

 

二、灵敏度分析

　　　　分析某参数对结果的影响，我们首先可以分析参数大致的波动范围（波动幅度小于10%，即风险率小于10%）。确定现有参数的取值是否合理。

 

 

 

　　在此基础上，用相对该变量衡量结果的敏感程度。建立数学模型：

 

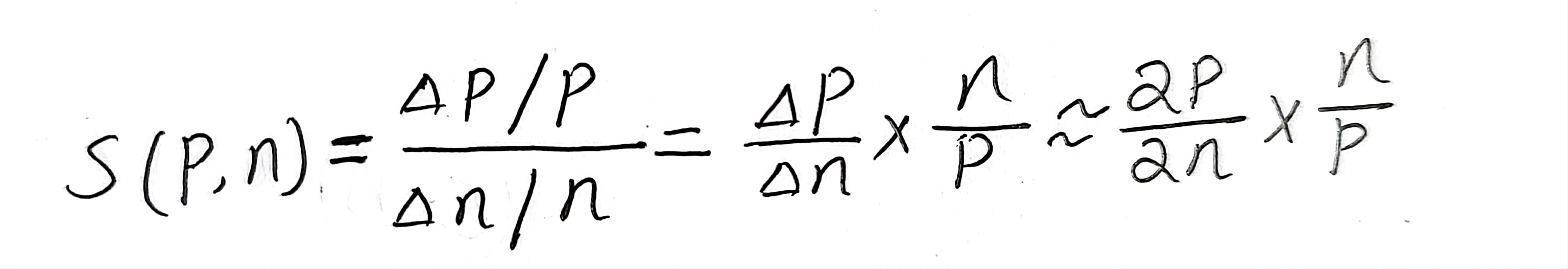
　　该模型表示当系数变化百分比时，相应的结果变化百分比。

 

三、参数改变对结果的影响

　　当考虑参数对结果的影响时，需要把参数也作为一个自变量建立函数关系，绘制出参数取不同值时对应的函数图像。

　　相关代码为：

%参数变化对函数图像的影响
clc,clear,close all
p=1.5:0.001:2.5;
n=3000;
Q=-10*n.*p.^2+(80000+15*n)*p-120000;
subplot(331)
plot(p,Q);
xlabel('n=3000')
n=4000;
Q=-10*n.*p.^2+(80000+15*n)*p-120000;
subplot(332)
plot(p,Q)
xlabel('n=4000')
n=5000;
Q=-10*n.*p.^2+(80000+15*n)*p-120000;
subplot(333)
plot(p,Q)
xlabel('n=5000')
n=6000;
Q=-10*n.*p.^2+(80000+15*n)*p-120000;
subplot(223)
plot(p,Q)
xlabel('n=6000')
n=7000;
Q=-10*n.*p.^2+(80000+15*n)*p-120000;
subplot(224)
plot(p,Q)
xlabel('n=7000')
n=3000:1000:7000;
p=(80000+15*n)./(20*n)