企业销售额问题——多元回归模型，DW检验

企业销售额问题

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

总结

一、回归分析

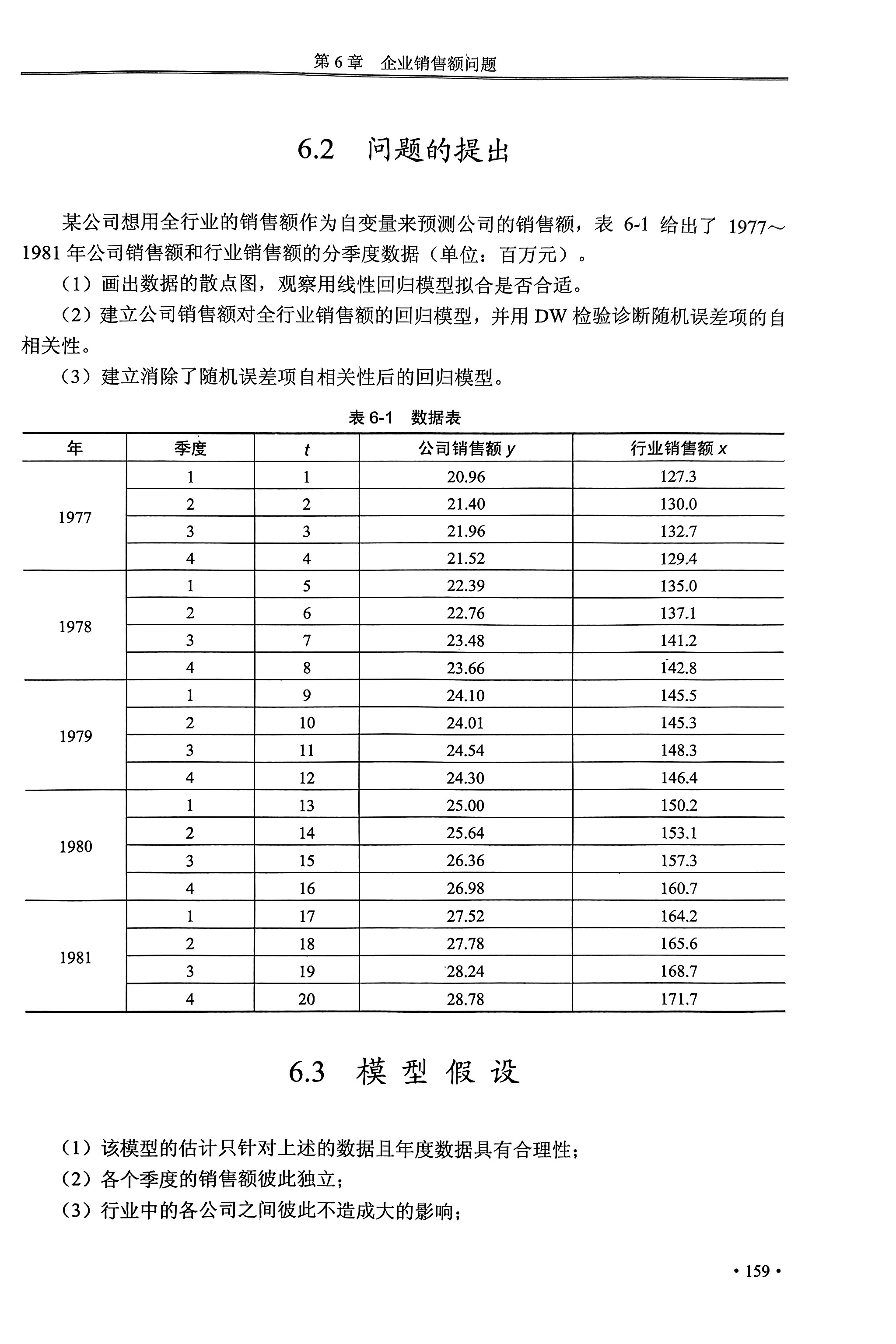
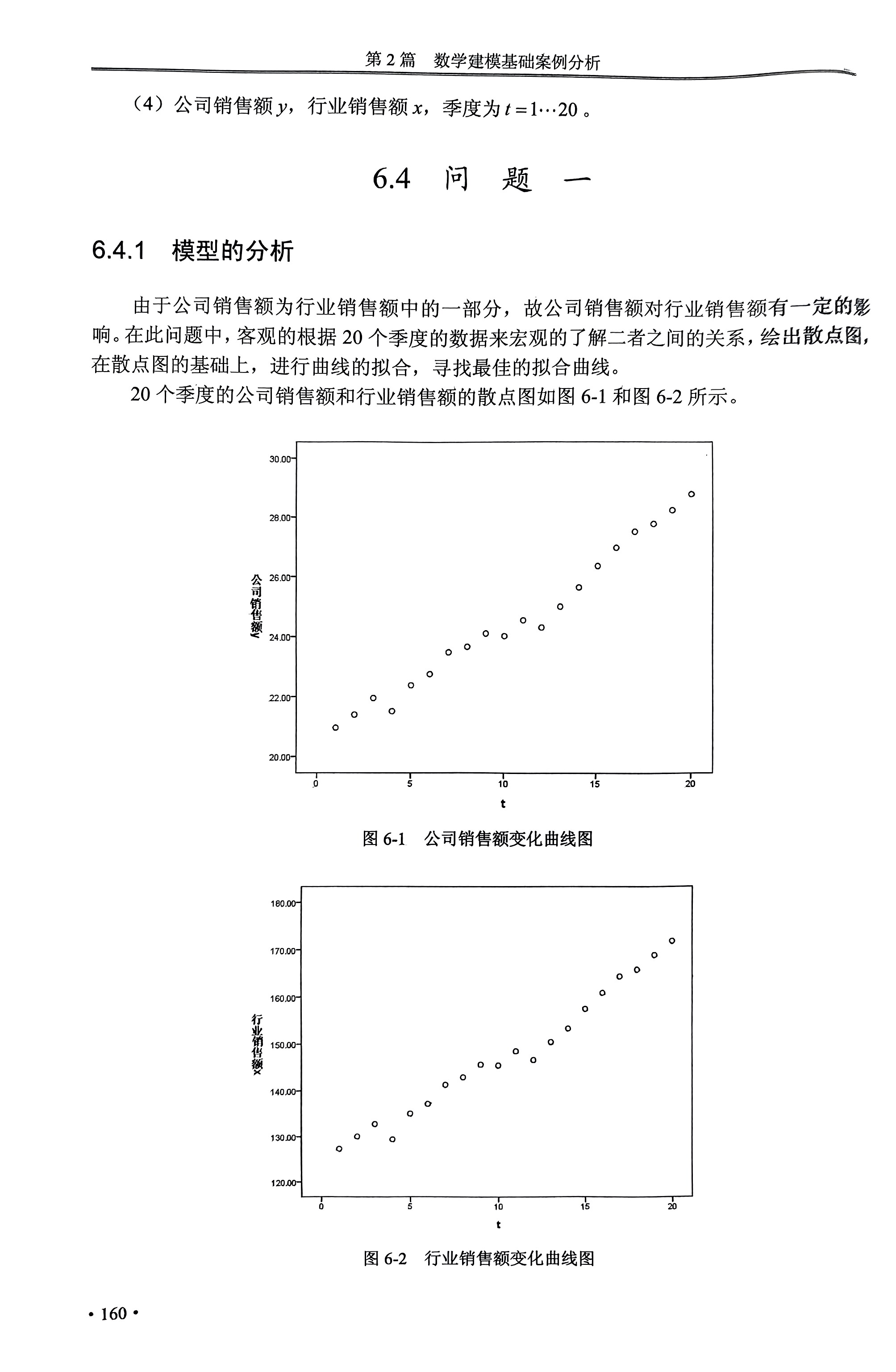
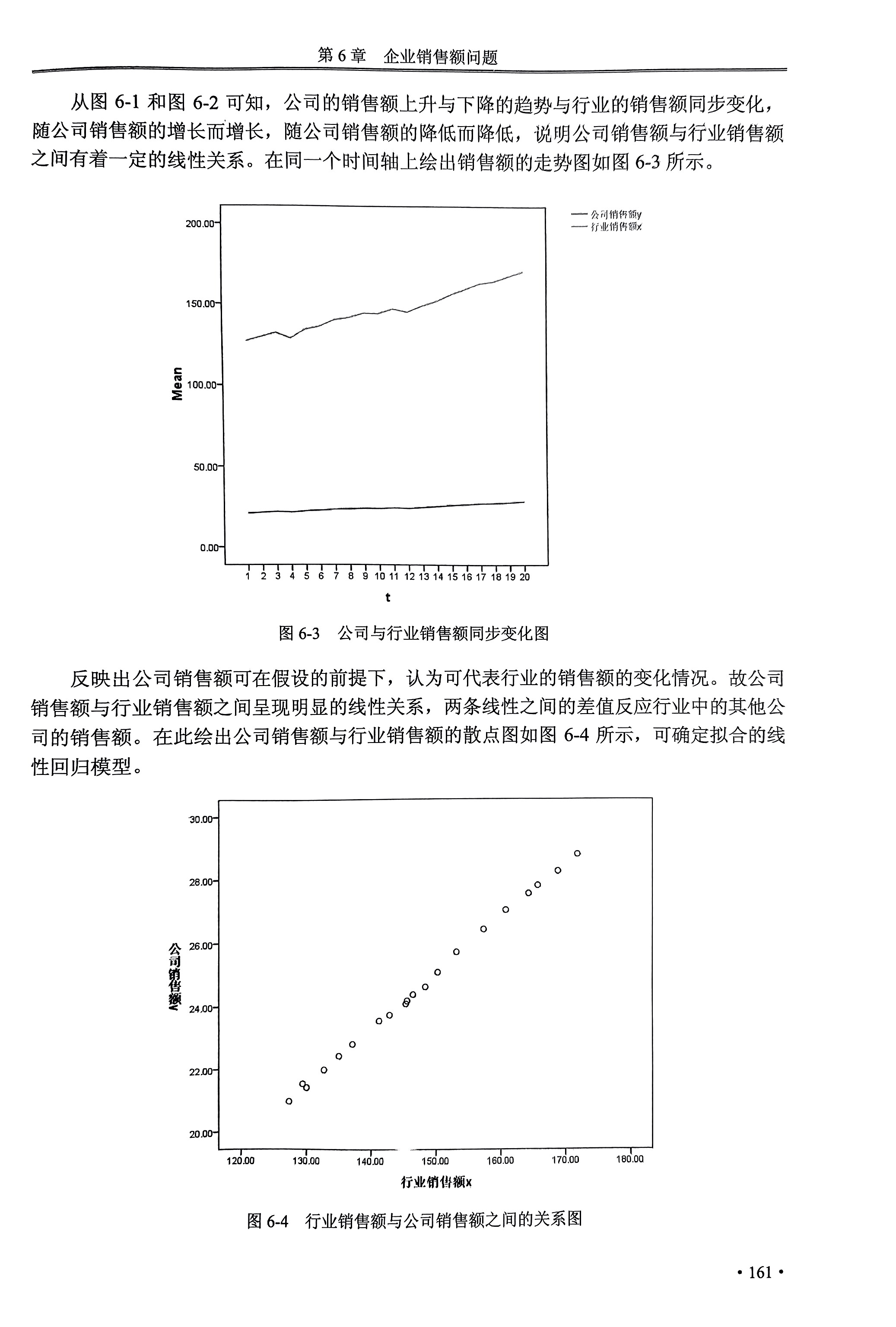
　　先绘制两个变量各自的散点图和相对散点图，找到单变量的变化规律以及变量间的相对关系（正相关，负相关或其他）。

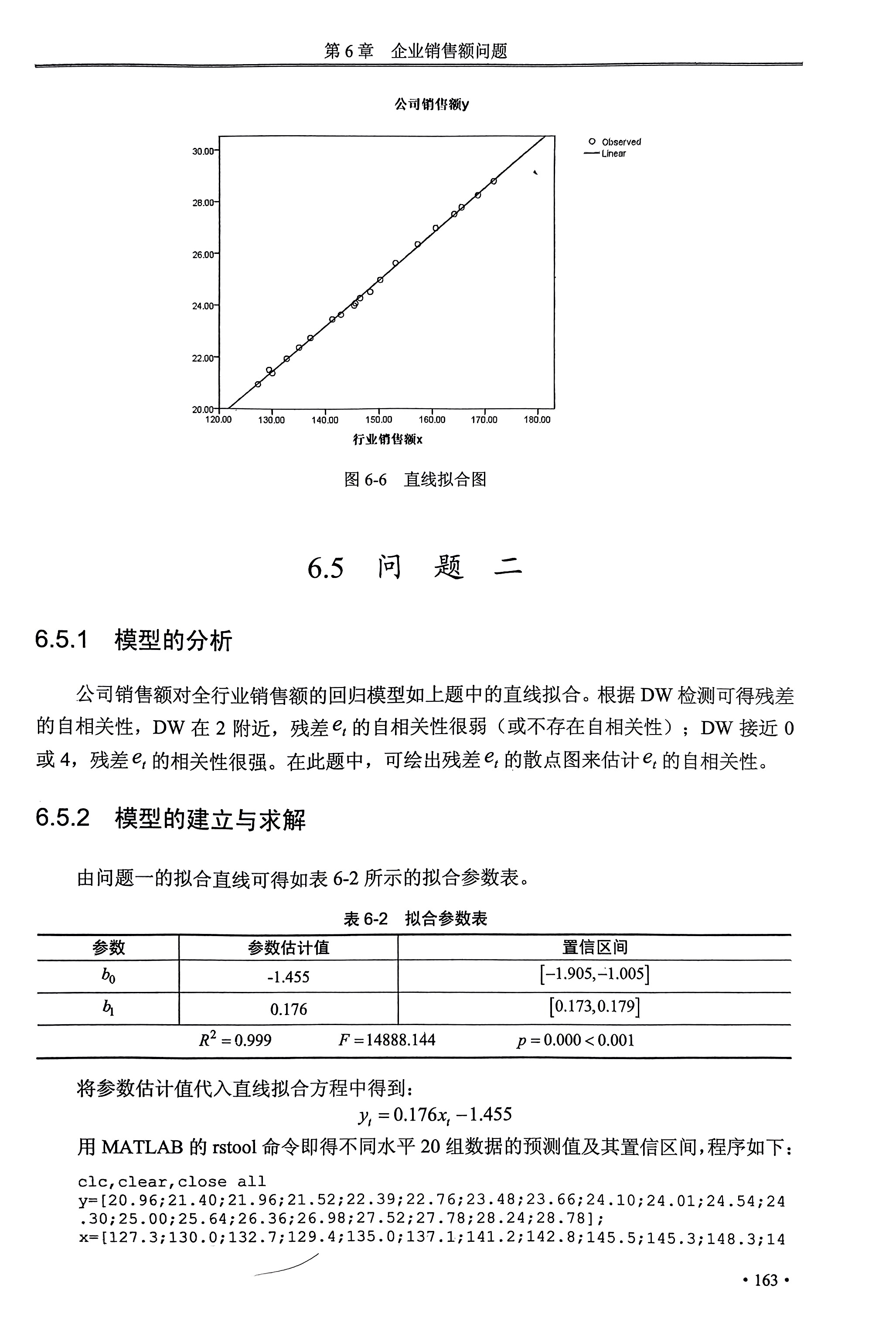
　　根据变量间的相对关系对数据进行函数拟合，运用多种拟合函数（相关性要一致），通过检验拟合程度最好的模型，得到其对应的拟合函数。

 

二、例题特点

　　所给数据是一个时间序列，具有周期性，检验时需要对该模型进行自相关性检验，即DW检验，来说明此问题是否是一个经济滞后性的数学模型。

　　DW检验原理与算法流程（上文已给出）

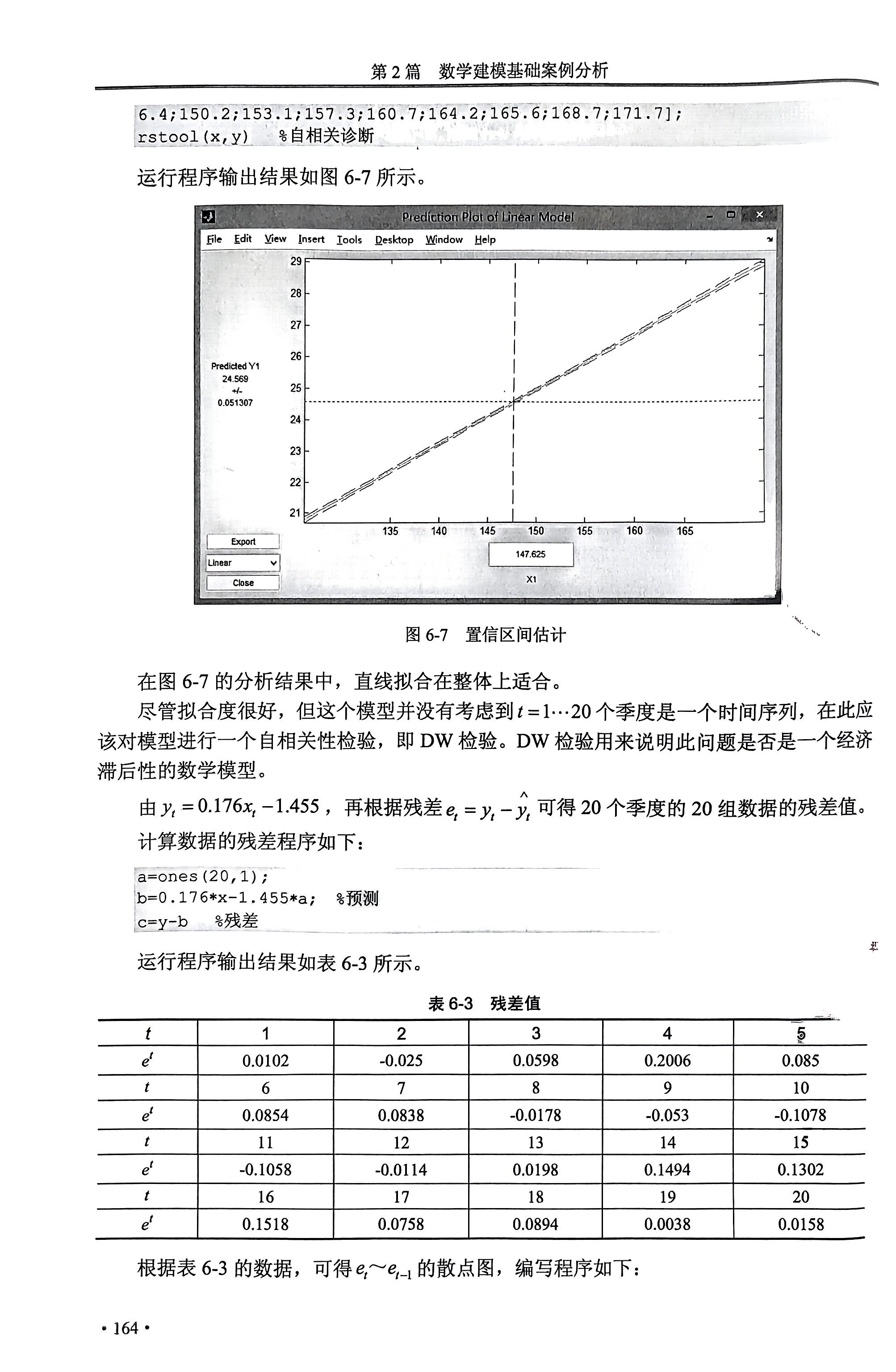
　　结果分析：

　　DW是给咱家样本容量N和解释变量数目K，在给定显著性水平下，建立DW检验统计量的上下界临界值，确定了具体的用于判断的范围。

　　DW判定规则为：

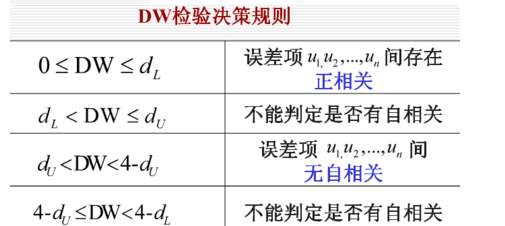
　　其中，dl和du通过查找DW检验上下界表得到（已知样本数N，变量数K，显著性水平a）。

 

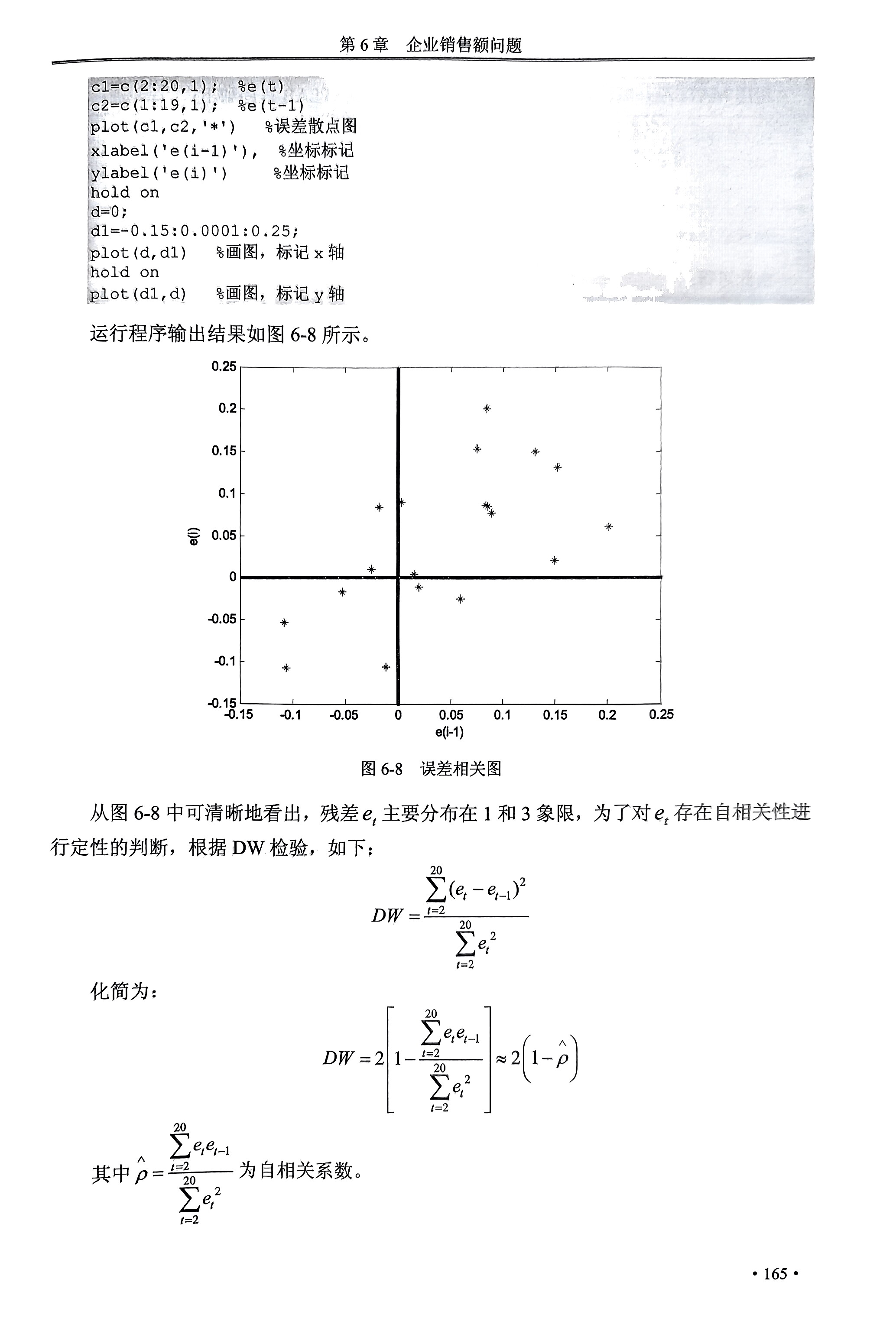
相关程序：

%DW检验（用于时间序列自相关性检验）
clc,clear,close all

%导入数据
y=[20.96;21.40;21.96;21.52;22.39;22.76;23.48;23.66;24.10;24.01;24.54;24.30;25.00;25.64;26.36;26.98;27.52;27.78;28.24;28.78];
x=[127.3;130.0;132.7;129.4;135.0;137.1;141.2;142.8;145.5;145.3;148.3;146.4;150.2;153.1;157.3;160.7;164.2;165.6;168.7;171.7]; 

%自相关检验
rstool(x,y) 

%计算残差
a=ones(20,1);
b=0.176*x-1.455*a;%预测（用得到的回归函数）
c=y-b;            %残差

%残差e(t)相对于e(t-1)的散点图
c1=c(2:20,1);   %e(t)
c2=c(1:19,1);   %e(t-1)
plot(c1,c2,'*')
xlabel('e(i-1)'),
ylabel('e(i)')
hold on
d=0;
d1=-0.15:0.001:0.25;
plot(d,d1)  %画图，标记x轴
hold on
plot(d1,d)  %画图，标记y轴

% DW的程序：
num=c(1:19)'*c(2:20);  %误差乘积
den=sum(c(2:20).^2);   %求和
p = num/den;           %p值
DW=2*(1-rou)           %DW值

 

三、滞后回归模型

　　在已知模型具有自相关性时，可对变量进行如下处理：

 

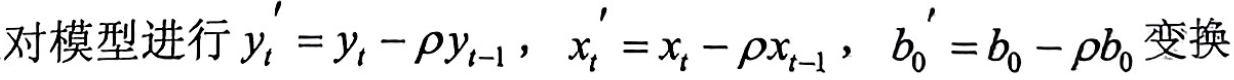
　　得到新的拟合函数：

 

 

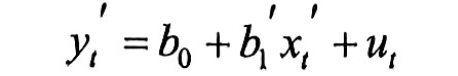
　　再次进行DW检验，相关代码如下

 

% 滞后回归模型的DW检验
clc,clear,close all

%导入数据，数据处理
y=[20.96;21.40;21.96;21.52;22.39;22.76;23.48;23.66;24.10;24.01;24.54;24.30;25.00;25.64;26.36;26.98;27.52;27.78;28.24;28.78];
y1=y(2:20,1); %y（t)
y2=y(1:19,1); %y(t-1）
y3=y1-0.71133*y2; %y'（t)，p由原始DW检验得到
x=[127.3;130.0;132.7;129.4;135.0;137.1;141.2;142.8;145.5;145.3;148.3;146.4;150.2;153.1;157.3; 160.7;164.2;165.6;168.7;171.7];
x1=x(2:20,1); %x（t)
x2=x(1:19,1); %x(t-1）
x3=x1-0.71133*x2; %x'（t),p由原始DW检验得到

%计算残差
a=ones(19,1);
y4=y3-0.173*x3+0.263*a  % 残差(根据新的回归函数，原始值-预测值）
y5=y4(2:19,1);       %e(t)
y6=y4(1:18,1);       %e(t-1)
y7=y5-y6;            %差值

y8=sum(y7.^2)       %求和
y9=sum(y5.^2)       %求和
DW= y8/y9           %DW值
p=1-DW/2            %p值