P6774 时代的眼泪

名人名言

一道非常优秀的分块入门题，值得分块初学者花时间思考，不值得一写。

—— \(\tt{B}\color{red}{Fqwq}\)

Section -1

好吧，虽然前半句令人不适，后半句说的还是挺对的。

NOI 2020 之后就一直想切这个题……没办法，谁叫我是时代的眼泪呢……

一开始一直沿用 Yuno loves sqrt tech I 的方法做这题，最后发现虽然有一些迁移性，但还是有较大差异的。

如果您没有切 Yuno loves sqrt tech I，强烈建议你先去做那个题，至少口胡一遍。

由于下标会比较多，本文在超过一个下标的时候会采用多元函数形式表示数组，以拯救笔者和读者的眼睛。

Section 0

• 定义 \(F(l,r,x,y)\)：\((l,r,x,y)\) 这个询问的答案。

• 定义 \(G(L,R,x,y)\)：第 \(L\) 到 \(R\) 块块间答案。

• 定义 \(lp\)：块的最左边。

• 规定下文的 \([l,r]\) 只包含 \([l,r]\) 内的整数。

Section 1

序列分块，块长 \(\sqrt n\)，序列内离散化。

Section 2

接下来的套路就比较寻常了，我们先把左右散块分开得到一张经典图。

然后不难发现有三种块间贡献：散块对整块（红 \(\to\) 蓝），整块对散块（蓝 \(\to\) 绿），散块对散块（红 \(\to\) 绿），整块对整块（一块中的蓝 \(\to\) 另一块的蓝）。

然后不难发现除了这几种贡献，我们还有散块和整块间（同块 \(\to\) 同块）的贡献，一共 \(6\) 种。

这六种贡献加起来，就是答案了（如果左右端点在同块则只记为一个散块统计）。

接下来我们一个一个来算。

Section 3

我们先考虑散块内部的贡献。

现在的规模已经变成 \(\sqrt n\) 了（即下标，值域都 \(\leq\sqrt n\)），因此可以暴力记录 \([lp,i]\) 的数中小于等于 \(y\) 的有几个。

• 定义 \(rk_i\) 为 \(i\) 的块内从小到大排名。
• 定义 \(pre(i,r)\) 为 \([lp,i]\) 中 \(rk\) 小于 \(r\) 的数的数量。

我们对于每一块都预处理这一块的 \(pre\) 数组，一个块的复杂度为 \(\sqrt n\times\sqrt n\)，总复杂度为 \(O(n\sqrt n)\)。

然后我们可以拆 \(F(l,r,x,y)=F(l,r,1,y)-F(l,r,1,x-1)-\sum\limits_{i=l}^r[x\leq a_i\leq y]pre(i,lb_x-1)\)。

稍微推一下就可以得到 \(F(l,r,1,y)=\sum\limits_{i=l}^r[a_i\leq y]pre(i,rk_i)\)。单次询问复杂度 \(O(\sqrt n)\)。

Section 4

散块对散块的贡献。

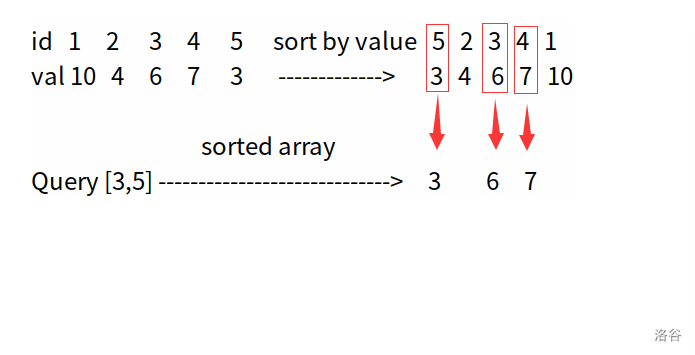
这类是最简单的，由于两边都只有 \(\sqrt n\) 个数，提取出来排序后归并计算顺序对即可。如果我们对每块预先根据值排序，然后只对所有数判断是否需要提取出来，单次询问复杂度就可以消掉 \(\log\)，即 \(O(\sqrt n)\)。这个 trick 和 Yuno loves sqrt tech I 是一样的，具体可以看这张图。

Section 5

整块对整块的贡献。

由于只有 \(\sqrt n\) 个块，我们还是可以暴力。

• 定义 \(PRE(i,r)\) 为前 \(i\) 块中小于等于 \(r\) 的数的个数。

预处理的时间复杂度为 \(O(n\sqrt n)\)。

然后我们根据散块间贡献那个式子的形式分解一下，假设我们求第 \([L,R]\) 块的贡献。

\(G(L,R,x,y)=G(L,R,1,y)-G(L,R,1,x-1)-\sum\limits_{i=L}^RP_iQ_i\)。

其中 \(P_i\) 代表 \([L,i)\) 块中 \(<x\) 的数的个数，\(Q_i\) 代表第 \(i\) 块 \(\in[x,y]\) 的数的个数。由于 \(P_i\) 和 \(Q_i\) \(PRE\) 已经处理好了，于是后面的东西可以 \(O(\sqrt n)\) 算。

而前面我们就要再次利用之前的一个性质了：一个块只有 \(\sqrt n\) 种不同的数。我们将 \(PRE\) 数组转化成块内贡献。

• 定义 \(bpre(i,r)\) 为 \(i\) 所在块之前的所有数中小于 \(i\) 这块从小到大第 \(j\) 个数的数量。
• 定义 \(lb(i,j)\) 为在 \(i\) 所在块所有元素中比 \(j\) 小的最大元素的从小到大排名。

不难发现并不需要预处理 \(bpre\) ，可以根据 \(rk\) 在 \(PRE\) 中查询，\(lsh\) 可以单块 \(O(n)\) 处理，总时间复杂度 \(O(n\sqrt n)\)。

有了这两项，我们就可以预处理 \(G(L,R,1,y)\) 了。

• 定义 \(bans(i,L,r)\) 为 \([1,L]\) 块与第 \(i\) 块从小到大前 \(r\) 个元素组成的逆序对数量。

显然 \(bans(i,L,r)=\sum\limits_{j\in\text{block}}[rk_j\leq r]bpre_{L,rk_j}\)，然后这玩意可以前缀和，单块 \(O(n)\)，整体 \(O(n\sqrt n)\)。

\(G(L,R,1,x)=\sum\limits_{i=L+1}^R bans(i,i-1,lb(i,x))-bans(i,L-1,lb(i,x))\)，因此单次询问 \(O(\sqrt n)\)。

Section 6

散块对整块的贡献和整块对散块的贡献。

这两部分并不难，由于只有 \(\sqrt n\) 个数，我们只要判断每个数和中间的所有整块能组成的逆序对即可。

我们可以将所有整块中 \([l,r]\) 的出现次数用 \(PRE\) 在 \(O(1)\) 的时间内求出来，对于散块中的数一个一个求逆序对数量即可，单次询问 \(O(\sqrt n)\)。

Section 7

整块块内的贡献。

由于 \(x\) 和 \(y\) 在每块离散化之后只有 \(\sqrt n\times \sqrt n\) 种选择，所以我们考虑把所有情况都算出来。

• 定义 \(Pre(i,x,y)\) 为第 \(i\) 块取从小到大第 \(x\) 到 \(y\) 个元素组成的逆序对数量。

这部分是可以通过 \(pre(i,r)\) 暴力预处理的，单块 \(O(n)\)，总时空复杂度 \(O(n\sqrt n)\)。

Section 8

综上，我们在 \(O(n\sqrt n)\) 的时空复杂度内在线解决了这个问题……

这个题实现起来逻辑清晰，但是代码有一点点细节和一点点长度，在洛谷上有一点点卡常。

为了卡常我特判了第 \(10\) 个数据点并在那个点用了 Yuno loves sqrt tech II 的代码。

然而如果您不像我一样人傻常数大应该马上就能卡过去吧。