OO第一单元作业——表达式的解析与简化
OO第一单元作业——表达式的解析与简化
一、任务描述与实现思路
这一单元的作业旨在让我们完成表达式的解析与简化,那么很自然地,处理流程就可以分为解析与简化两个部分。第一阶段是解析,即识别表达式,项,和因子,并将其从一个字符串的形式转化为我们可以进行直接处理的数据结构;第二阶段是简化,即合并同类项使得输出字符串的长度尽量短。对于一个表达式,项,或因子,在解析完成后我们即可进行简化,因此总体来说,这两个阶段是并行的。
在自己的不断尝试和与同学们的交流中,我逐渐认识到递归下降处理法是解决表达式问题的最佳之法,递归下降法的基本思路是:对于一个表达式,根据加减号的位置将其分割为不同的项;对于一个项,根据乘号的位置将其分割为不同的因子;对于一个因子,如果是基本因子,就直接进行解析与化简,如果是表达式因子,就再将其当成一个新的表达式进行解析。一个项里的所有因子都解析完成后,就可以通过相乘来得到这个项的解析结果;同样地,一个表达式里的所有项都解析完成后,就可以通过相加减来得到这个表达式的解析结果。下面我将以这一单元的三次作业为例,具体讲讲这个思路是如何实现的。
第一次作业
第一次作业中,指导书规定的因子只包括常数因子,变量因子和表达式因子,而且括号的深度最多为一层,因此递归下降思路的优势不明显。在这次作业中,我借鉴了课上实验提供的思路:如果一个表达式中没有括号,那么在这个表达式中,只靠寻找加号和减号就可以分割不同的项;在一个项中,只靠寻找乘号就可以分割不同的因子。那么,我们可以非常简单地对一个没有括号的表达式进行解析。现在,我们拿到的是一个有单层括号的表达式,那么只需要将所有的单层括号展开,就可以把相对较难的问题转化为一个我们可以解决的问题。
那么我们就面临一个问题:如何拆括号?根据指导书中的提示,我将括号分为四类:第一类是一个不与其他因子相乘的,不带幂次的表达式因子,如+(x + 2 * x +1);第二类是一个常数或者一个幂函数乘以一个表达式因子,如2*(x+1)、x*(x + x+1)、x**+2*(x + 3);第三类是两个括号表达式相乘,如(x+2)*(x+3);第四类是一个带幂次的表达式因子,如(2*x + 3)**2。分好类以后,就该考虑处理的顺序了。由于乘方运算的优先级最高,所以我们应该先处理第四类括号,对此,我的处理方法是:将带幂次的表达式因子转化为多个相同的不带幂次的表达式因子的乘积,如将(2*x + 3)**2转化为(2*x + 3)*(2*x + 3),这样就将第四类括号转化为了第三类括号。接着,同时处理第二类括号和第三类括号,即将括号外面的内容分配给括号里的每一项,这样就将所有括号都转化为了第一类括号。对于第一类括号的处理,直接将括号外面的正负号分配给括号内的每一项,就可以拆括号了。
在一个表达式中,我们需要识别其中的括号。如果仅仅是检测括号的位置与左右括号的匹配关系,那么在遍历表达式的过程中,用一个栈来记录相应信息就可以了。但是我们现在还需要判断一个括号属于上面的哪种类型,于是就需要用到正则表达式匹配。我对每种类型的括号都设计了相应的正则表达式,如第四类括号的正则表达式为:(?<bracket>\\([0-9x\\+\\-*$\\s]*\\))\\s*\\$\\$\\s*\\+?\\s*(?<exp>\\d*),在后续的括号处理过程中,我仅仅对字符串进行了更改,没有使用任何数据结构来存储相应的层次信息。图1直观地展示了我对表达式中括号的处理流程:
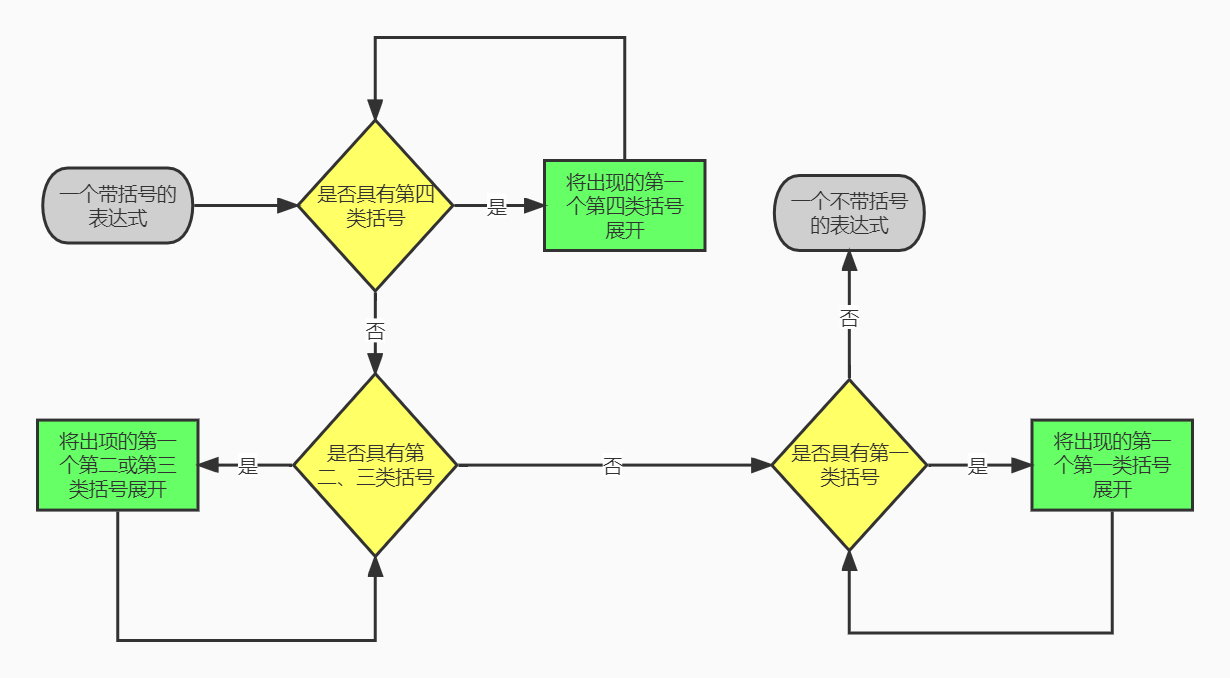
图1 拆括号流程
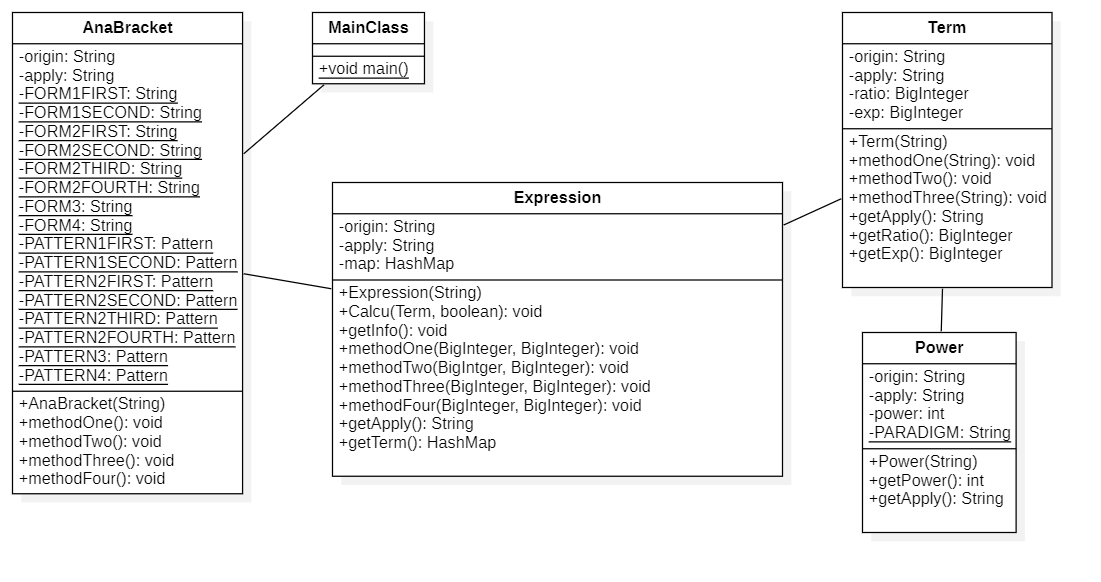
图2 作业一类图
通过上面的描述,我们已经可以看出,这种拆括号法虽然原理简单,容易想到,但是十分繁琐,且没有有效利用Java语言面向对象的特点,其本质还是C语言中面向过程的处理方法。而且,长而晦涩的正则表达式字符串不利于人阅读与检验,容易出错。不过,现在我们既然已经将一个带括号的表达式转化为一个不带括号的表达式,就可以按照本小节第一段提到的思路继续处理了。
项是由因子相乘得到的,而我们已经处理了表达式因子,剩下的就只有幂函数因子和常数因子了,因此我把项的简化结果设置为A*x**B,在表达式中的项处理完毕后,根据不同项返回的参数B进行同类项合并,最后输出结果即可。
图2是本次作业的类图。这里对其中的各个类的成员变量的成员方法进行简单解释。AnaBrackct类用来处理括号,其中一系列String类型的静态变量就是我们所需要的正则表达式,后面的Pattern类型变量与之一一对应。这个类中的mathodOne()到methodFour()分别用来处理四类括号。Expression类中的methodOne()至methodFour()和Term类中的methodOne()至methodThree()用来化简输出形式。不同的类中均有名为origin和apply的String型私有变量,分别用来存储初始字符串和化简后的结果。Power里中的名为power的int型变量表示幂函数的指数,PARADIGM是幂函数的正则表达式字符串。另外,这些类中还有一系列get方法,用来访问类中的私有成员变量。
根据类图可以看到,在我的设计中,没有涉及到类之间的继承和多态关系,且类之间的调用关系单一,没有摆脱面向过程的思维方式。在类的内部设计中,方法名设计不妥,无法直观地看到其作用。本文后面有我的代码行数分析表,总体上来说各个类的代码行数还算合理,但是由方法复杂度分析表和类的复杂度分析表可以看到,我的方法复杂度普遍较高,且类之间耦合度大,不利于代码功能的扩展或修改,这也是我在第二次作业中选择重构的原因之一。
这次作业有一些小坑点。比如表达式的形式化描述中,规定了每个表达式的第一个项和每个项的第一个因子之前可以带一个正负号,常数因子可以是带符号整数,因此我们在解析表达式时,不能简单地根据加减号来分割项,而是要判断一下我们遇到的加减号到底是用来连接不同的项,还是仅仅用来表示正负。在解析项时也是一样,幂次符号"**"包含两个乘号,因此我们也必须在遇到乘号时看一下这是不是指数符号再继续解析。对于我采用的这种解析方式,字符串处理拆括号环节是最容易出错的环节,由于正则表达式长而复杂,并且字符串处理流程繁琐,稍不注意就可能导致处理前后的字符串不相等。在互测环节中,我就因为没有识别出以下情况而别hach:- -(-44*x**5-89* 23 *26),其中两个减号共同作用于这个括号,并且它们之间有一个制表符。因此在后面的作业中,我注重正则表达式字符串的简洁性,这样可以有效避免从表达式形式的角度被hack。
第二次作业
第二次作业中,因子除了可以是常数,幂函数,表达式,还可以是自定义函数,求和函数,三角函数。由于上次作业中出现的种种缺陷,我选择了重构,按照递归下降的思路来实现解析与简化。我分别设计用来解析表达式的类,用来解析项的类和用来解析因子的类。对于七种因子:常数、幂函数、括号、自定义函数、求和函数、cos、sin,分别设计类来进行解析。其中,常数类、幂函数类、cos类、sin类隶属于单一因子接口,其解析返回值是一个因子;括号类、自定义函数类、求和函数类隶属于表达式因子接口,其返回值是一个表达式。每个类实现对应的接口,使类之间的关系更加明确。在项解析类中和在表达式解析类中所做的输出简化工作与作业一相同,只不过需要我们进行相乘或相加操作的是多个ArrayList容器(其中的每一个变量代表返回表达式中的一个项),其操作方法将在后面介绍。
在第一次作业的总结中,我认识到了正则表达式字符串处理问题的优缺点:当正则表达式简洁易懂时,加之捕获组的使用,我们可以很容易地对所有情况进行分析和讨论,并提取其中的有效内容;当正则表达式繁琐时,往往会漏掉一些符合形式化表述但又有些极端的表达式形式,从而导致很难发现的bug。在这次作业中,我对每个因子使用正则表达式判定,这样比判断括号容易得多。比如:正弦函数的正则表达式是“sin\\((?<argv>.*)\\)\\$\\$\\+?(?<exp>\\d+)”或者“sin\\((?<argv>.*)\\)”;求和函数的正则表达式是“sum\\(i\\,(?<start>[+-]?\\d*)\\,(?<end>[+-]?\\d*)\\,(?<func>.*)\\)”。相信采取递归下降法设计的同学所使用的正则表达式都与我的非常接近。这样就做到了对不同因子的准确判定。
既然这个方法的名字叫“递归下降法”,那么显而易见,我们要做两件事:递归和下降。递归是比较好理解的,对于括号表达式,求和函数和自定义函数,将其展开后当成一个新的表达式进行处理,得到这个新的表达式的处理结果,然后将这个处理结果当成是这个因子的化简结果,返回给项解析类。这里的展开其实还是字符串处理过程。对于括号表达式,其展开方式与第一次作业中我对第四类括号的处理方式相同。对于求和函数和自定义函数,则涉及到用实参替换形参的问题,这里面有三个需要注意的地方。第一,在对求和函数的展开过程中,对于求和函数sum(i, 1, 3, sin(i)),我们不能简单地用求和变量i的取值来替换求和表达式中的字母‘i’,否则“sin”中的‘i’也会被替换,导致无法继续解析;第二,在自定义函数的调用过程中,对于f(x, y) = x*y这类的多自变量函数,我们需要先对形参x进行替换,以免在对其他形参替换时引入了新的字母‘x’;第三,在自定义函数的调用过程中,假设我们有这样一个函数:f(x) = x**2,我们调用时使用的实参是f(x**2),那么我们在替换时必须用括号将替换的内容括起来:(x**2)**2,否则将会得到x**2**2这样的无法解析的式子。
那么“下降”是如何做到的呢?这也是我在第二次作业中的一个创新点。我以这样一个表达式为例:(x + 1) * (x + 1) + 2,在表达式中分割项的过程其实就是找加减号的过程,在第一次作业中,我需要对找到的加减号进行判断,来确定该符号是不是用于分割不同项,但是这样的判断过程繁琐而易错。在这次作业中,我取消了这样的判断过程,而是采用抛出和处理异常的方式来解析表达式。对于上面的表达式,当我们解析到第一个加号时,已经遍历过的部分“(x”将会被传入项解析类,但是很明项这不是一个项,是无法解析的,于是项解析类抛出一个异常。表达式解析类接收到这个异常,表明该加号不是用于分割项的,于是便继续向后扫描字符串,第二个加号的处理过程类似。当扫描到第三个加号时,“(x + 1) * (x + 1)”被传入项解析类,项解析类尝试对这个字符串按项的格式进行解析,显然这个字符串是符合项的形式化描述的,项解析类可以对其进行解析。表达式解析类没有接收到异常,于是判定这个加号是用于分割项的。我对该方法命名为“尝试解析法”,这种方法在第三次作业中仍在沿用。图三展示了尝试解析法的流程,图四是递归下降法的整体思路。
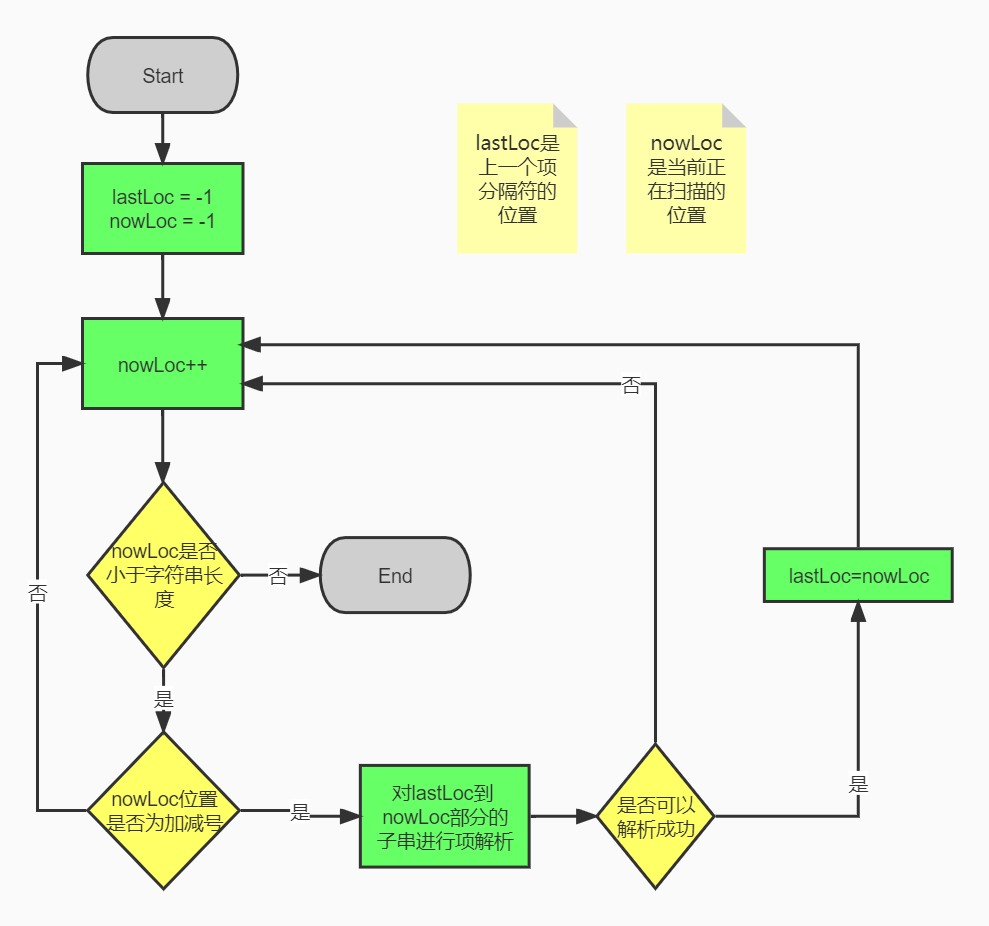
图3 尝试解析法
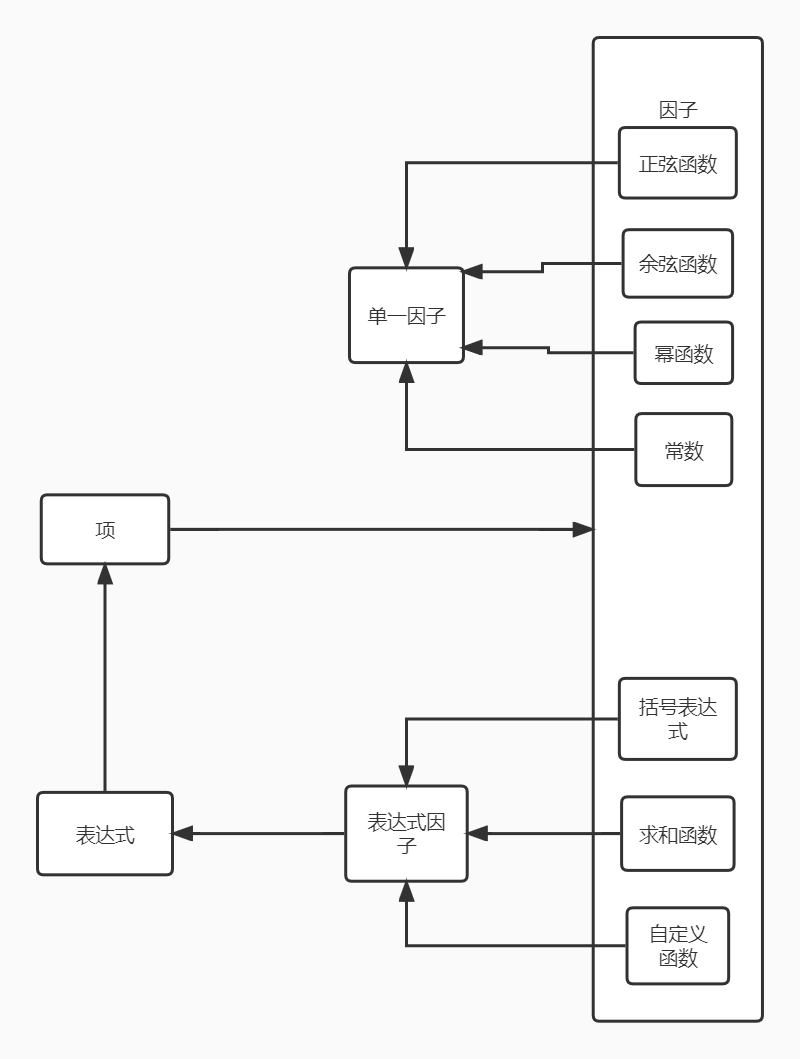
图4 递归下降法
接下来我们需要关注一个具体的问题:表达式因子接口与单一因子接口的差异何在?首先要明确一点:正弦函数,余弦函数,幂函数与常数因子的解析结果还是一个因子,因此也是一个项;而括号表达式,求和函数,自定义函数的解析结果是一个表达式,其中包括多个项。而每个项都可以写成这样的形式:A*x**B*∏(cos(argv)**exp)*∏(sin(argv)**exp),因此我设计了一个Term类来存储一个项,其中包括两个BigInteger类成员分别存储A和B,两个HashMap类成员分别存储一系列sin和cos类型因子,并以argv为key值,以exp为value值。于是,单一因子类的解析返回值就是一个Term类变量,而表达式因子类的解析返回值就是一个ArrayList<Term>容器,其中的Term变量为相加关系。这样一来,对项的化简就变成了对两个ArrayList<Term>的乘法(或者一个Term与一个ArrayList<Term>的乘法),对表达式化简就便成了对两个ArrayList<Term>的加法(或者一个Term与一个ArrayList<Term>的加法)。对于这些计算,我设计了两个底层方法:第一个是两个Term的乘法,第二个是把一个Term加入ArrayList<Term>中并合并同类项,对两个ArrayList<Term>的操作只需要不断调用者两个底层方法就可以了。
到此,第二次作业的设计就完成了。下图是我的代码类图,相比于第一次作业,我的设计复杂了很多,一方面是代码功能的扩展所致,另一方面,我从面向过程的设计思路转变为面向对象的设计思路,有所不适应,导致我的设计冗长而缺乏简洁性。在第三次作业中,我虽然没有进行重构,但是对设计结构进行了整改,以满足程序设计时需要遵守的一些原则。
 图5 作业二类图
图5 作业二类图
在上图中,Term类与所有其他类都有组合关系,因此我在图中没有体现。根据类图可以看到,这样的设计初步满足了Java语言面向对象的编程思想。但是,我对表达式本身的结构特性并没有理解地很到位。相比于我的设计,一个更好的设计思路是把自定义函数的结构化过程和对自定义函数的调用过程分开在不同的类中实现,比如把调用自定义函数的方法放在一个名为FunctionCall的类中;同样地,可以把对两个Term或两个ArrayList<Term>进行计算的所有方法放在一个名为TermCalculation的类中。将数据存储与数据计算分离,满足类的单一职责原则。
在第二次作业中,我的方法复杂度相比第一次有很大程度地下降,但是方法数量与总代码行数增长速度过快。我尽量使每个方法的功能单一化,并且方法之间的调用关系简单化,这就不可避免地造成了每个类中方法数的不受控增长。递归下降法的使用为第三次作业打下了程序的架构基础,但是具体实现思路的混乱又使得我在扩展功能时不得不重新分析代码结构,并做一些优化。
由于此时我对递归下降法的了解还不深入,在这次作业的中测进阶样例中出现bug,未能进入互测环节,且强测也没有找出这个bug。
第三次作业
第三次作业相比于第二次作业又增加了一些功能,比如自定义函数可以递归调用、自定义函数调用的形参可以是求和函数等,递归解析的要求越来越高,使得这次作业几乎只能使用递归下降法来处理。得益于第二次作业建立的良好架构,我在本次作业的完成过程中并未重构,但由于第二次作业中我对一些类设计不合理,使得我的代码修改量并不小。
第二次的递归下降解析法可以处理第三次作业中的全部表达式,但是在处理因子时,除了匹配正则表达式外,还应该添加一些额外的判定方法。比如,我设置三元函数调用的正则表达式为:“(?<name>[fgh])\\((?<argvOne>.*)\\,(?<argvTwo>.*)\\,(?<argvThree>.*)\\)”,如果不考虑捕获组的使用,正则表达式可以简化为“[fgh]\\(.*\\,.*\\,.*)”。是如果调用时的情况是“f(sum(i, 1, 2, i), f(x, cos(x), sin(x)), x)”呢?这个因子里有这么多逗号,如果只使用正则表达式来匹配,我们无法知道哪个逗号是用来分割不同因子的。于是,我们只能再次使用尝试匹配法。比如,我们可以从这么多个括号里选出两个括号,假定他们是用来分割最外层自定义函数的因子的,把这种分割方式下得到的三个参数做进一步的解析,如果能解析成功,就说明我们的分割是正确的;否则就说明逗号的选择错误,我们需要尝试其他逗号的组合。但是,我这次使用了另外一种检验尝试的方法——括号匹配法。下图是括号匹配法的流程:
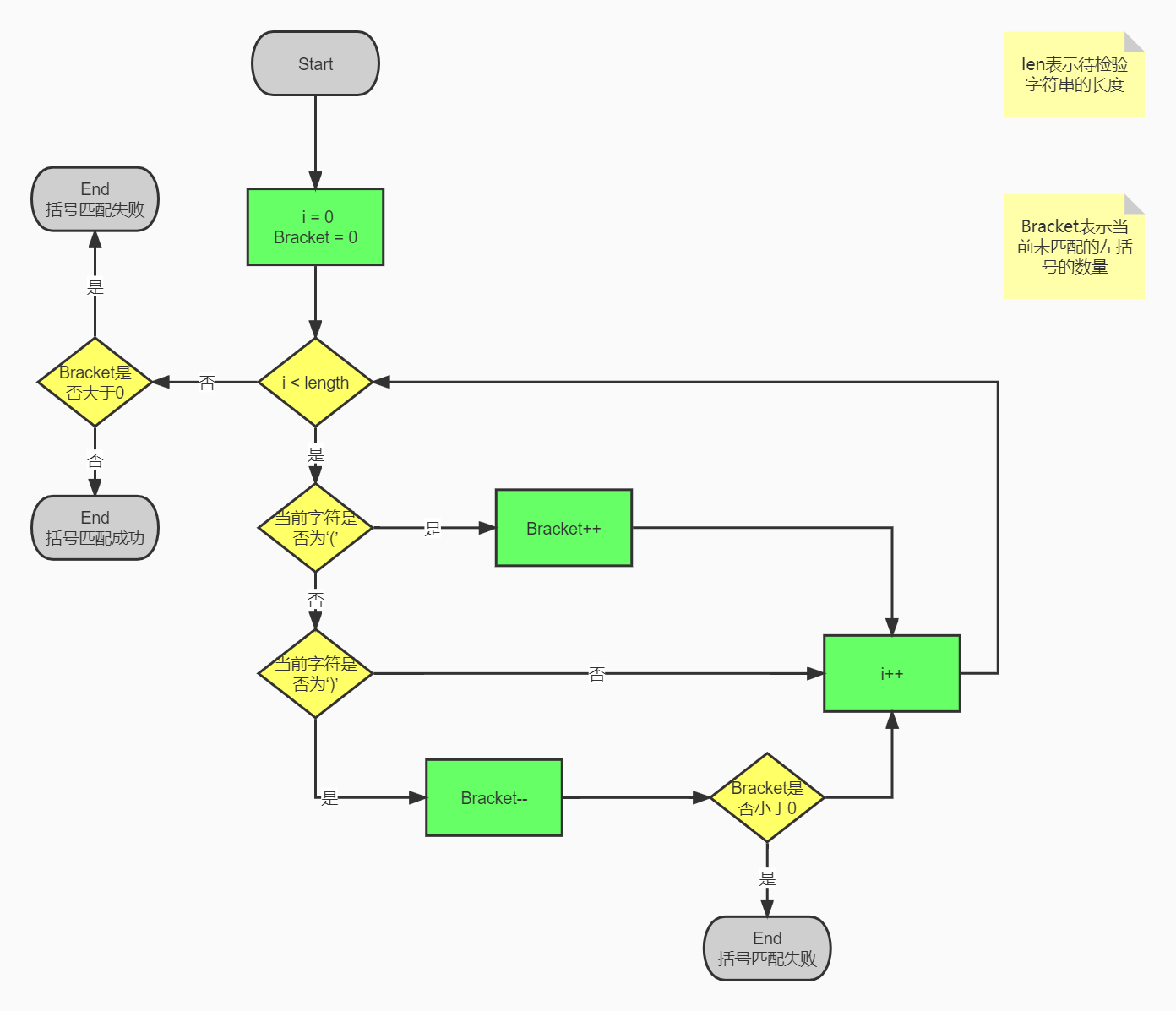
图6 括号匹配法
简而言之,括号匹配法使用了栈的数据结构,查看一个字符串中左括号和右括号是否匹配。那么对于我的尝试解析法,我选定两个括号后,通过字符串分割得到三个子串,接下来对这三个子串进行括号匹配,如果它们都能匹配成功,那么我们就可以认为当前的分割是正确的,可以进行下一步的解析了。当然,这里默认了一点,就是对于一个子串,如果括号匹配成功,那么就说明它是一个正确的表达式。我所能想到的所有例子都满足这个论断,但是我并不能从理论上证明其正确性。后来,我在中测,强测和互测中都没有出现解析错误,那么就姑且认为这种解析方式是正确的吧!下图展示了我上面的分割过程,即尝试匹配法在参数分割时的应用:
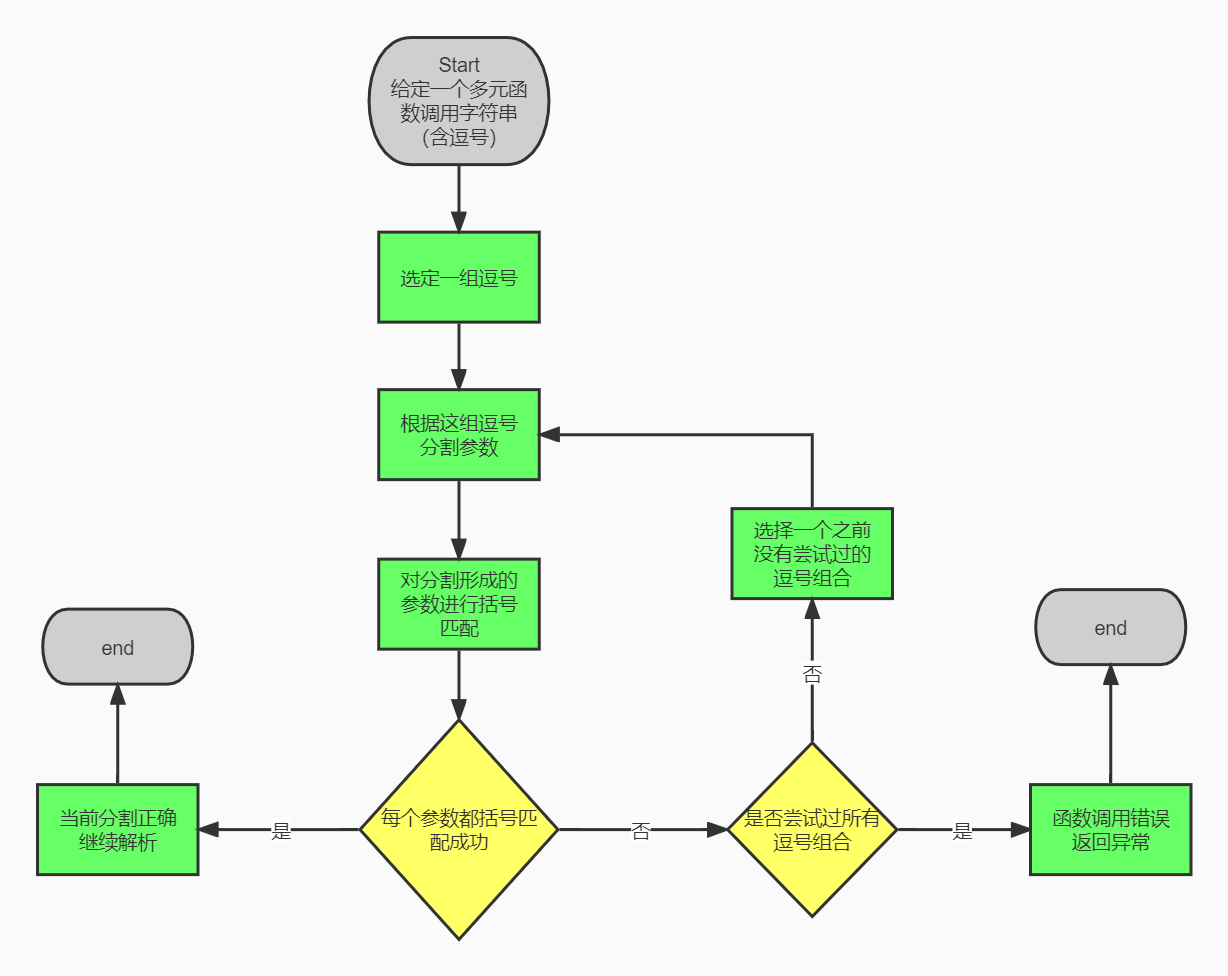
图7 逗号匹配法
对于一个三元函数,若函数调用时总共出现了n个逗号,则在最差的情况下需要匹配n*(n-1)/2次,因此这种匹配方法的复杂度是O(n2)。我在这里再提出一种复杂度为O(n)的匹配算法,原理和我的尝试匹配法相同,但每个逗号只需遍历一次,更高效。这个方法来源于和同学的讨论。
对于每个逗号,我们考虑上一个用于分割参数的逗号(如果没有,就取最外层函数调用时的左括号)到它之间的子串,如果这个子串括号匹配成功,那么这个逗号也是用于分割参数的逗号,否则就不是。当我们遍历完整个字符串后,如果我们提取到的用于分割参数的逗号数量不等于自定义函数形参数量减一,则说明函数调用错误,需要返回异常;如果等于,那就按照我们之前找到的那一组逗号来分割参数,然后对于这些参数继续解析。下图展示了这种方法的流程:
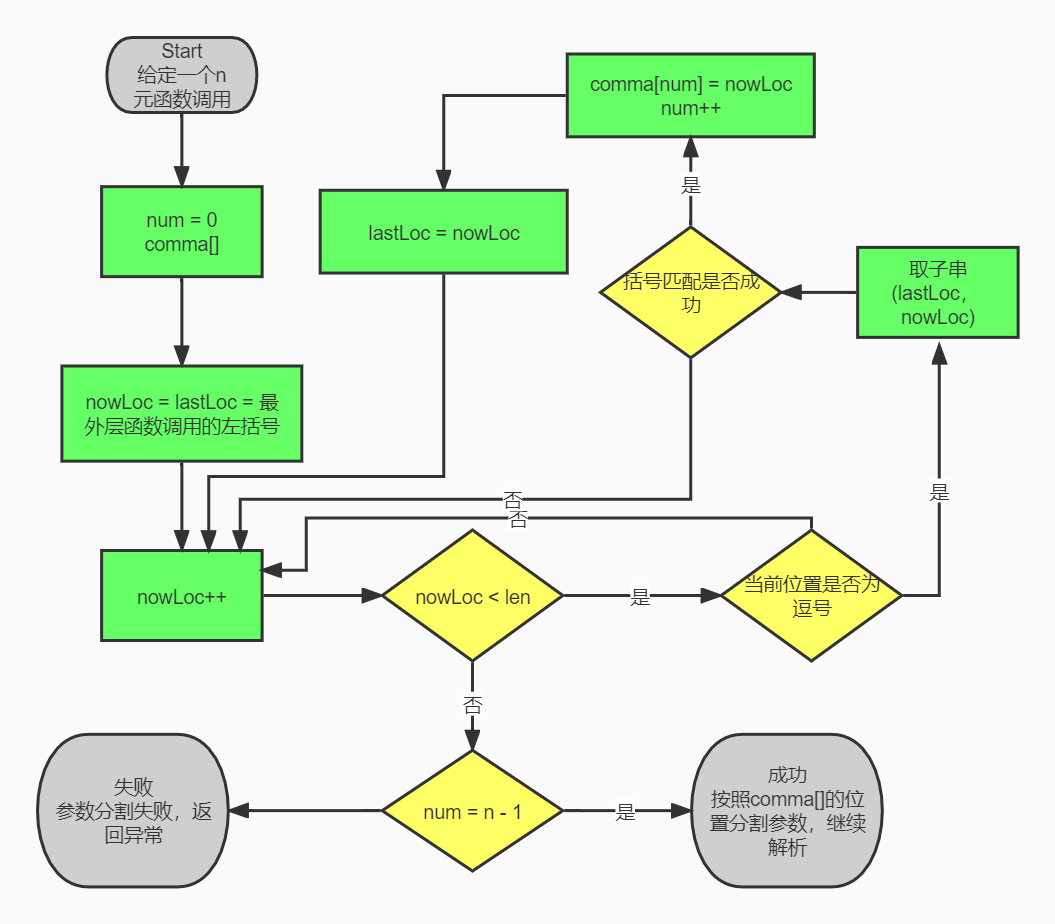
图8 逗号遍历法
接下来我展示一下第三次作业的设计类图:

图9 第三次作业类图
相比于第二次作业,我将Term类的里的方法分成两组:第一组是有关Term类变量本身属性方面的操作,这些方法留在Term类中;另一组是有关Term类变量之间的计算操作,这些方法转移到AnaTerm类中。同样,有关函数调用的方法和自定义函数本身的属性方法被分离,FunctionCall类专门处理自定义函数调用操作。除此之外,还新增了一个Caller类,用来传递自定义函数调用的匹配关系和参数分割结果。由于Term类,AnaTerm类和AnaBracket类(括号匹配法)与几乎其他所有类都有组合关系,因此在图中并未展现。要说在结构上还有什么可以改进的地方,我觉得可以设计一个三角函数类,里面实现所有三角函数共有的属性和方法,sin和cos只需继承这个三角函数类即可。在图中可以看到,sin和cos类中有大量重复的属性和方法,大大降低了代码的可扩展性和易读性。
尝试解析法容易想到和理解,但是其缺点也是显而易见的:类之间的耦合度会随着问题的规模增大和处理情况的增加而增加,有方法复杂度分析表和类的复杂度分析表可以看到,即使我对一些类的结构做了整改,但是复杂度仍有所上升。由于我的实现基本满足了单一职责原则,因此我认为,复杂度的上升来源于尝试解析时的分支复杂性。分支设计过于复杂不利于跟踪程序的运行过程,且容易出现死循环,无限递归等异常情况。
前面说到了,顶层方法通过捕获底层方法抛出的异常来判断当前的尝试是否正确。这里的“顶层”和“底层”是相对的,每一个需要使用尝试解析法来分割字符串的方法,其执行结果都依赖于所有下层方法的运行结果。当这个字符串很长时,递归的嵌套层次将会很深,如果解析错误,我们很难跟踪到底是在哪一层解析过程出了问题。而且,随着递归的嵌套层次逐步增加,尝试的次数成指数型增长,不利于处理复杂度过高的字符串。
最后说一下测试结果:在强测环节,我的代码出现了一个bug。三角函数内部只能是因子,因此cos(-x)是不合法的,必须将其转化为cos((-x)),这个bug也在互测环节中被多次hack。由于时间原因,我未能仔细阅读别人的代码,提交测试点的时候也只是提交了我在debug过程中构造的测试点,无法成功hack别人。
二、学习心得与体会
在连续三次作业的迭代开发中,代码的可扩展性成为判断是否需要重构的关键因素。对于我在第一次作业中大量使用的字符串处理,需要枚举所有的情况,且仅仅是根据“括号嵌套层数最多为一层”的要求而设计的,可扩展性差,且容易出错,在递归的要求出现时,是必须重构的。第二次作业中,我设计了利于扩展的代码架构,但是由于Term类和Function类中的功能过多,不符合单一职责原则,因此在第三次作业中还需要对这两个类进行整改。总体来说,我对第三次作业的设计还是比较满意的,我基本上接受了面向对象的思维方式,也开始在代码的设计中注重可扩展性,可维护性与易读性。但是由于思路的不清晰,造成的代码的冗长繁琐,其中的一大部分原因是我不愿意也不敢对第二次作业的代码做过多的修改。代码的扩展或修改对已有代码的结构和风格有一种破坏作用,我们在对已有代码进行扩展或修改时,必须注重维护代码的原有设计风格,这样才能持续迭代,否则当代码的可读性下降到一定程度时,就很难继续迭代了。比如如果我们还要在表达式中继续添加其他三角函数因子,如tan,cot等,那么我的三角函数部分就又需要整改了。在迭代开发中,最好的一种做法是对需要扩展的模块进行代码风格整改,而对其他部分不作修改,这样方能在逐次迭代中不断优化风格,又不致使一次作业的工作量过大。
程序的鲁棒性是另一个重要的检验标准。以往我总是喜欢面向评测机编程,设计的代码几乎只能处理评测机中的测试点,但是本次作业中明确指出了,可能出现不符合形式化标准的表达式,这需要我们的程序做出判断,输出“Wrong Format”或其他信息,而不是直接抛出运行时错误。我的尝试解析法正好可以处理此类情况,并在main函数捕获到异常时输出对应信息,这也是尝试解析法的一个优点。
代码风格检查工具使我很不适应,尤其是“每个方法最多60行”的要求。在第一次作业中,我基本采用的还是面向过程的编程思路,于是很难做到这一点,经常有一个方法需要写200行左右。我只能把这200行分开,放在四个顺序执行的方法里分别完成,这就是为什么我的类图中出现了methodOne、methodTwo、methodThree、methodFour这样的方法名。在后两次作业中我发现,只要每个方法都满足单一职责原则,其实60行还是很容易做到的。尽管如此我还是建议把标准放宽一点,比如80行,如果我们需要为了提高代码风格得分而特意修改,就有违本要求的初衷了。
三、代码架构分析图
第一次作业方法复杂度分析表
| CogC | ev(G) | iv(G) | v(G) | |
|---|---|---|---|---|
| formal.Term.Term(String) | 6.0 | 1.0 | 5.0 | 5.0 |
| formal.Term.methodTwo() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.methodThree(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.methodOne(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getRatio() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getApply() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Power.Power(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Power.getPower() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Power.getApply() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.MainClass.main(String[]) | 4.0 | 1.0 | 4.0 | 4.0 |
| formal.Expression.methodTwo(BigInteger, BigInteger) | 3.0 | 3.0 | 3.0 | 3.0 |
| formal.Expression.methodThree(BigInteger, BigInteger) | 4.0 | 3.0 | 3.0 | 4.0 |
| formal.Expression.methodOne(BigInteger, BigInteger) | 3.0 | 3.0 | 3.0 | 3.0 |
| formal.Expression.methodFour(BigInteger, BigInteger) | 4.0 | 3.0 | 3.0 | 4.0 |
| formal.Expression.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Expression.getInfo() | 7.0 | 3.0 | 7.0 | 7.0 |
| formal.Expression.getApply() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Expression.Expression(String) | 24.0 | 1.0 | 4.0 | 19.0 |
| formal.Expression.calCu(Term, boolean) | 8.0 | 1.0 | 4.0 | 4.0 |
| formal.AnaBracket.methodTwo() | 18.0 | 1.0 | 8.0 | 12.0 |
| formal.AnaBracket.methodThree() | 9.0 | 1.0 | 5.0 | 5.0 |
| formal.AnaBracket.methodOne() | 38.0 | 1.0 | 11.0 | 14.0 |
| formal.AnaBracket.methodFour() | 10.0 | 1.0 | 3.0 | 5.0 |
| formal.AnaBracket.AnaBracket(String) | 2.0 | 1.0 | 2.0 | 3.0 |
| Total | 140.0 | 35.0 | 76.0 | 103.0 |
| Average | 5.6 | 1.4 | 3.04 | 4.12 |
第二次作业方法复杂度分析
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| formal.Term.Term(Term) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.Term.Term(Sin) | 5.0 | 1.0 | 2.0 | 3.0 |
| formal.Term.Term(PowerFunc) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.Term(Cos) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.Term.Term(Constant) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.negate() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.mulTerm(Term) | 16.0 | 7.0 | 9.0 | 9.0 |
| formal.Term.makeVariable() | 11.0 | 2.0 | 10.0 | 11.0 |
| formal.Term.makeOutput() | 13.0 | 1.0 | 5.0 | 7.0 |
| formal.Term.isZero() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getVariable() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getSinFac() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getMulResult(ArrayList, ArrayList) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.Term.getExpX() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getCosFac() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getConstant() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.calCu() | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.Term.addTerm(ArrayList) | 6.0 | 4.0 | 6.0 | 6.0 |
| formal.Term.addConstant(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseTerm.ParseTerm(String) | 13.0 | 3.0 | 7.0 | 9.0 |
| formal.ParseTerm.mulTerms(ArrayList) | 3.0 | 2.0 | 3.0 | 3.0 |
| formal.ParseTerm.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseSum(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.parseSin(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.parsePowerFunc(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseFunction(String, Function) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.ParseFactor(String) | 20.0 | 10.0 | 13.0 | 14.0 |
| formal.ParseFactor.parseCos(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.parseConstant(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseBracket(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.getOutput() | 4.0 | 1.0 | 3.0 | 4.0 |
| formal.ParseExpr.ParseExpr(String) | 3.0 | 1.0 | 2.0 | 3.0 |
| formal.ParseExpr.makeOutput() | 12.0 | 3.0 | 8.0 | 10.0 |
| formal.ParseExpr.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseExpr.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseExpr.findTerm() | 12.0 | 3.0 | 4.0 | 8.0 |
| formal.ParseExpr.addTerm(ParseTerm, boolean) | 5.0 | 1.0 | 5.0 | 5.0 |
| formal.MainClass.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.MainClass.getFunctionList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sum.Sum(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sum.isType(String) | 5.0 | 2.0 | 3.0 | 5.0 |
| formal.factor.Sum.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sum.calCu() | 2.0 | 2.0 | 3.0 | 3.0 |
| formal.factor.Sin.Sin(String) | 7.0 | 1.0 | 6.0 | 6.0 |
| formal.factor.Sin.isType(String) | 6.0 | 2.0 | 4.0 | 6.0 |
| formal.factor.Sin.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getSp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getArgv() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.argvAna() | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.factor.PowerFunc.PowerFunc(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.PowerFunc.isType(String) | 6.0 | 2.0 | 4.0 | 6.0 |
| formal.factor.PowerFunc.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.PowerFunc.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.use(String, String, String) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.factor.Function.use(String, String) | 2.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Function.use(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.isCall(String) | 11.0 | 5.0 | 11.0 | 14.0 |
| formal.factor.Function.Function(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.factor.Function.call(String) | 3.0 | 3.0 | 3.0 | 3.0 |
| formal.factor.Cos.isType(String) | 6.0 | 2.0 | 4.0 | 6.0 |
| formal.factor.Cos.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getSp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getArgv() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.Cos(String) | 5.0 | 1.0 | 4.0 | 5.0 |
| formal.factor.Cos.argvAna() | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.factor.Constant.mulConstant(BigInteger, BigInteger) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Constant.isType(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Constant.getValue() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Constant.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Constant.Constant(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Bracket.parseBracket(String, BigInteger) | 2.0 | 2.0 | 3.0 | 3.0 |
| formal.factor.Bracket.isType(String) | 7.0 | 3.0 | 4.0 | 7.0 |
| formal.factor.Bracket.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Bracket.Bracket(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| Total | 214.0 | 120.0 | 203.0 | 236.0 |
第三次作业方法复杂度分析表
| CogC | ev(G) | iv(G) | v(G) | |
|---|---|---|---|---|
| formal.Term.Term(Term) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.Term.Term(Sin) | 5.0 | 1.0 | 2.0 | 3.0 |
| formal.Term.Term(PowerFunc) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.Term(Cos) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.Term.Term(Constant) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.Term(BigInteger, BigInteger, HashMap, HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.setInfo(String, String, boolean) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.negate() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.isZero() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getVariable() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getSinFac() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getExpX() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getCosFac() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.getConstant() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.Term.addConstant(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseTerm.ParseTerm(String) | 14.0 | 3.0 | 8.0 | 10.0 |
| formal.ParseTerm.mulTerms(ArrayList) | 3.0 | 2.0 | 3.0 | 3.0 |
| formal.ParseTerm.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseSum(String) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.ParseFactor.parseSin(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.parsePowerFunc(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseFunction(Caller) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.ParseFactor.ParseFactor(String) | 14.0 | 10.0 | 9.0 | 10.0 |
| formal.ParseFactor.parseCos(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.ParseFactor.parseConstant(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.parseBracket(String) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.ParseFactor.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseFactor.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseExpr.ParseExpr(String) | 4.0 | 1.0 | 3.0 | 4.0 |
| formal.ParseExpr.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseExpr.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.ParseExpr.findTerm() | 12.0 | 3.0 | 5.0 | 8.0 |
| formal.ParseExpr.addTerm(ParseTerm, boolean) | 4.0 | 1.0 | 4.0 | 4.0 |
| formal.MainClass.main(String[]) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.MainClass.getFunctionList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sum.Sum(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Sum.isType(String) | 1.0 | 2.0 | 1.0 | 2.0 |
| formal.factor.Sum.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sum.calCu() | 3.0 | 2.0 | 4.0 | 4.0 |
| formal.factor.Sin.Sin(String) | 6.0 | 1.0 | 4.0 | 5.0 |
| formal.factor.Sin.isType(String) | 2.0 | 2.0 | 2.0 | 3.0 |
| formal.factor.Sin.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getSp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getOutput() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.getArgv() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Sin.argvAna() | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.factor.PowerFunc.PowerFunc(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.PowerFunc.isType(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.PowerFunc.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.PowerFunc.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.FunctionCall.useTwo(Caller) | 3.0 | 1.0 | 2.0 | 3.0 |
| formal.factor.FunctionCall.useThree(Caller) | 4.0 | 1.0 | 3.0 | 4.0 |
| formal.factor.FunctionCall.useOne(Caller) | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.factor.FunctionCall.judgeTwo(String, int) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.FunctionCall.judgeThree(String, int, int) | 1.0 | 1.0 | 3.0 | 3.0 |
| formal.factor.FunctionCall.isCall(String, Function) | 16.0 | 8.0 | 10.0 | 11.0 |
| formal.factor.FunctionCall.callTwo(String, Function) | 6.0 | 3.0 | 3.0 | 5.0 |
| formal.factor.FunctionCall.callThree(String, Function) | 9.0 | 4.0 | 4.0 | 6.0 |
| formal.factor.FunctionCall.callOne(String, Function) | 2.0 | 2.0 | 1.0 | 2.0 |
| formal.factor.FunctionCall.call(Caller) | 4.0 | 3.0 | 3.0 | 4.0 |
| formal.factor.Function.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.getFunction() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.getArgvNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.getArgv() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Function.Function(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.factor.Cos.isType(String) | 2.0 | 2.0 | 2.0 | 3.0 |
| formal.factor.Cos.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getSp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.getArgv() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Cos.Cos(String) | 5.0 | 1.0 | 4.0 | 5.0 |
| formal.factor.Cos.argvAna() | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.factor.Constant.mulConstant(BigInteger, BigInteger) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Constant.isType(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Constant.getValue() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Constant.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Constant.Constant(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| formal.factor.Caller.isValid() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.getFunc() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.getArgvTwo() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.getArgvThree() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.getArgvOne() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.getArgvNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.Caller(String, Function, int, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.Caller(String, Function, int) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.Caller(String, Function) | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Caller.Caller() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Bracket.parseBracket(String, BigInteger) | 6.0 | 2.0 | 6.0 | 6.0 |
| formal.factor.Bracket.isType(String) | 2.0 | 2.0 | 2.0 | 3.0 |
| formal.factor.Bracket.getTermList() | 0.0 | 1.0 | 1.0 | 1.0 |
| formal.factor.Bracket.Bracket(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.AnaTerm.mulTerm(Term, Term) | 18.0 | 7.0 | 11.0 | 11.0 |
| formal.AnaTerm.makeVariable(Term) | 15.0 | 2.0 | 12.0 | 13.0 |
| formal.AnaTerm.makeOutput(BigInteger, String) | 13.0 | 1.0 | 5.0 | 7.0 |
| formal.AnaTerm.makeInfo(Term) | 1.0 | 1.0 | 1.0 | 2.0 |
| formal.AnaTerm.getOutput(ArrayList) | 10.0 | 1.0 | 7.0 | 9.0 |
| formal.AnaTerm.getMulResult(ArrayList, ArrayList) | 3.0 | 1.0 | 3.0 | 3.0 |
| formal.AnaTerm.addTermList(ArrayList, ArrayList) | 2.0 | 1.0 | 3.0 | 3.0 |
| formal.AnaTerm.addTerm(ArrayList, Term) | 6.0 | 4.0 | 6.0 | 6.0 |
| formal.AnaBracket.judgeBracket(String) | 7.0 | 4.0 | 3.0 | 6.0 |
| Total | 234.0 | 151.0 | 234.0 | 269.0 |
| Average | 2.27 | 1.47 | 2.27 | 2.61 |



