2020牛客NOIP赛前集训营-普及组（第四场）A B C

时间 题目链接：

　　签到题，还是比较简单的，我们可以将时钟化为分钟，再跟3小时30分钟相加，然后用最后的总分钟数对一天的总分钟数取余，在化为时钟跟分钟；

　　看代码：

　　

#include <iostream>
#include <cstdio>

using namespace std;
typedef long long ll;
const int ma = 1e5 + 7;
int n,m,num[ma];

int main()
{
    int d,m;
    scanf("%d:%d",&d,&m);
    n = d * 60 + m + 210;
    n %= 1440;
    d = n / 60,m = n % 60;
    if(d < 10)
        printf("0");
    printf("%d:",d);
    if(m < 10)
        printf("0");
    printf("%d",m);
    return 0;
}

石子 题目链接：

　　根据题目意思A只能拿走偶数个的石子，B只能拿走奇数个的石子，那么我们就可以考虑对于奇数或者偶数个的石子，A，B会怎么样？

　　　　　　奇数个的石子：首先对于A来讲，因为A只能拿走偶数个的石子那么A肯定不能将石子拿完，那最后只能被B拿走，那就说明可以不用考虑奇数个的石子了，因为不管怎么样最后肯定是被B拿走最后的石子，就比如有石子13，A分别可以拿2 、4、8、10、12，但是总有奇数留下使得A不能拿完，所以如果有奇数的石子那就可以忽略不计看偶数个的石子了，如果没有偶数个的石子，那肯定是B赢得比赛，因为A一定不可以拿完，直到最后所有的石子堆都变成奇数堆而不能走停止。

　　　　　　偶数的石子：对于A来讲，因为他是先手所以他可以把一堆全部拿走，或者留下一个更小的偶数，然后后手选择了，后手就可以选择把另一堆的偶数堆变成奇数堆，这样A肯定是赢不了的。比如有两堆的石子，数量分别是2,3.那么A先走的话，有两种选择，一是将选择第一堆，那第一堆就没了，B就可以选择将第二堆全部拿走了，这样B就赢了；第二种就是选择第二堆，那A只能拿走2个，第二堆就剩下1个了，那就剩下两个堆都是奇数堆了，那肯定是B赢了。

　　总结：如果有偶数堆的话，只要A没有将全部拿走，那B肯定会将偶数堆变成奇数堆的。如果所有的都是技术堆，那肯定是B赢了，因为A怎么也不可能将奇数堆拿完。所以就只有一种情况A可以赢得比赛，就是只有一个堆并且这个堆的数量为偶数，这样可以让B没法拿走，所以代码就很简单了。

　　但是千万要注意这是多组输入！！！我就是没看到要多组输入导致我只得了20分，唉。

　　

#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;
typedef long long ll;
const int ma = 1e5 + 7;
int n,m,num[ma];

int main()
{
    while(scanf("%d",&n) != EOF)
    {
        for(int i = 1;i <= n;i++)
        scanf("%d",num+i);
    if(n == 1 && !(num[1] & 1))
        puts("YES");
    else 
        puts("NO");
    }
    return 0;
}

 

C卡片 题目链接：

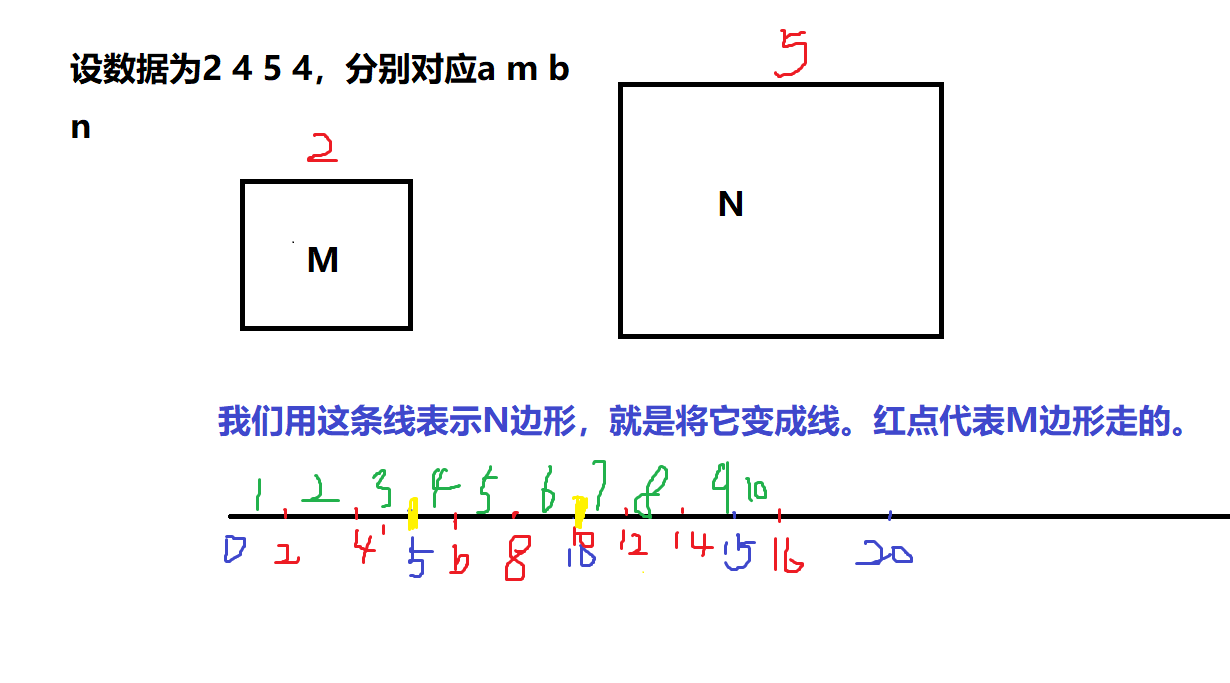
　　有一个正M边形，一个正N边形，让M边形在N边形上走，要求走到跟一开始的一样。那我们就可以分析。M边形走过的路程肯定是N边形周长的倍数，因为要走到跟一开始的一样，那M边形走的路程也是它边长a的倍数，对于M边形来讲，只要有一条边长跟一开始的完全一样就可以了，因为它是正多变形，那刻就可以假设是N边形周长C的x倍，是M边形边长A的y倍，那就是Cx = Ay了，那肯定是要求他们的最小公倍数了，这样他们相等了也就到了跟一开始完全相同的状态了，所以就可以知道要走多少遍N边形。

　　看样例1会发现有的点必须要旋转两次才可以，所以这样又不好算了，但是画一下图，你就会发现只有走过的路长为边长a，b的最小公倍数的时候，它就不会一个边要转折两次了，所以我们就只需要求这样点的个数就可以了。

　　

#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>

using namespace std;
typedef long long ll;
const int ma = 1e5 + 7;
const int mod = 1e9 + 7;
ll n,m,k;
string s;

ll gcd(ll a,ll b)
{
    return a % b ? gcd(b,a%b):b;
}
int main()
{
    ll a,b;
    cin >> a >> m >> b >> n;
    //求最小公倍数
    ll mul = a * b * n / gcd(a,b * n);
    // temp 为N边形的圈数
    ll temp = mul / (b * n);
    //len为要旋转的总长度，cnt用来计数
    ll len = temp * n * b,cnt = 0,c ;
    // num为长度可以化为多少个a
    ll num = len / a;
    c = a*b / gcd(a,b);
    //在总长度中找长度为lcm（a，b）倍数的值。
    for(int i = 0;i * c < len;i++)
    {
        cnt++;
    }
    //因为只有不是他们的倍数的点常需要两步走完一个点，也就是讲只要加上这么多个点就可以了。
    ll ans = num + temp * n - cnt; 
    cout<<ans<<endl;
    return 0;
}