剖析相机矩阵,第2部分:外在矩阵
欢迎来到系列“透视相机-互动之旅”的第三篇文章。 在上一篇文章中,我们学习了如何将相机矩阵分解为内在和外在矩阵的乘积。 在接下来的两篇文章中,我们将更详细地探讨外部矩阵和内部矩阵。 首先,我们将探索各种查看外部矩阵的方法,最后是一个交互式演示。
外在相机矩阵(The Extrinsic Camera Matrix)
相机的外部矩阵描述了相机在世界上的位置以及指向的方向。 熟悉OpenGL的人将其称为“视图矩阵”(或滚动到“模型视图矩阵”中)。 它有两个组成部分:旋转矩阵R和平移矢量t,但是正如我们将很快看到的那样,它们并不完全对应于相机的旋转和平移。 首先,我们将检查外部矩阵的各个部分,然后,我们将介绍更直观的描述照相机姿势的替代方法。
外在矩阵采用刚性变换矩阵的形式:左侧块为3x3旋转矩阵,右侧块为3x1平移列向量:
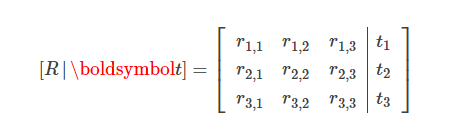
通常会看到此矩阵的版本,在其底部添加了(0,0,0,1)的额外行。 这使矩阵变成正方形,这使我们可以进一步将该矩阵分解为旋转,然后平移:
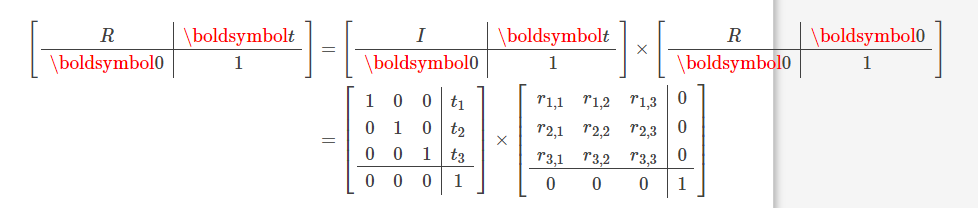
该矩阵描述了如何将世界坐标中的点转换为相机坐标。 可以将向量t解释为摄像机坐标中世界原点的位置,R列表示摄像机坐标中世界轴的方向。
关于外部矩阵要记住的重要一点是,它描述了世界如何相对于相机进行变换。 这通常是违反直觉的,因为我们通常要指定相机相对于世界的变形方式。 接下来,我们将研究两种更直观的描述相机外部参数的方法,以及如何将其转换为外部矩阵的形式。
从相机姿势构建外部矩阵(Building the Extrinsic Matrix from Camera Pose)
直接指定摄影机的姿势比指定世界点应如何转换为摄影机坐标通常更自然。 幸运的是,以这种方式构建外部相机矩阵很容易:只需构建一个描述相机姿势的刚性变换矩阵,然后将其取反即可。
令C为描述相机中心在世界坐标中的位置的列向量,令Rc为描述相机相对于世界坐标轴的方向的旋转矩阵。 然后,描述摄像机姿势的变换矩阵为[Rc | C]。 像以前一样,我们通过添加(0,0,0,1)的额外行来使矩阵平方。 然后通过反转相机的姿势矩阵来获得外在矩阵:
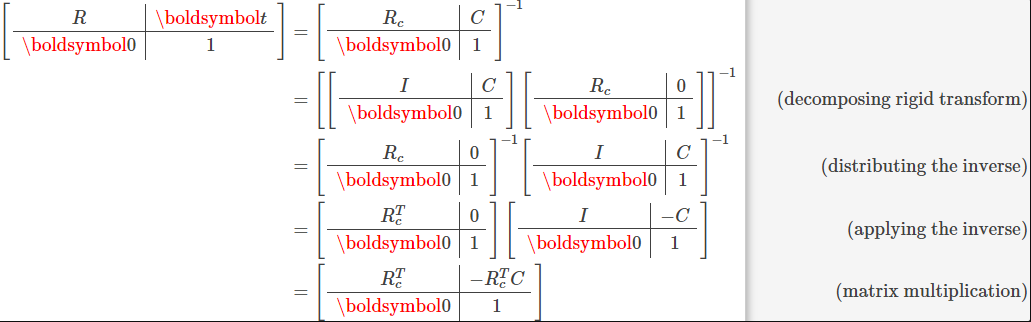
在应用逆矩阵时,我们使用了旋转矩阵的逆矩阵是转置的事实,而对转换矩阵求逆则只会抵消转换向量。 因此,我们看到外部矩阵参数与相机姿势之间的关系很简单:
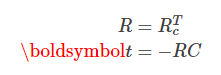
一些文本用-RC代替t编写了外在矩阵,该矩阵混合了世界变换(R)和相机变换表示法(C)。
“注视”相机(The "Look-At" Camera)
熟悉OpenGL的读者可能更喜欢使用以下三种方式指定摄像机的姿势:(a)摄像机的位置,(b)所看的东西以及(c)“向上”方向。 在旧版OpenGL中,这是通过gluLookAt()函数完成的,因此我们将其称为“旁视”摄像机。 令C为相机中心,p为目标点,u为向上方向。 用于计算旋转矩阵的算法为(摘自OpenGL文档):
- 计算L = p-C。
- 归一化L.
- 计算s = L x u。 (交叉商品)
- 规范化。
- 计算u'= s xL。
然后,外部旋转矩阵由下式给出:
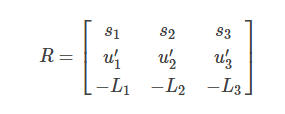
您可以通过与以前相同的方式获得转换向量,即t = -RC。
Try it out!
以下是交互式演示参数化相机外部参数的三种不同方式。 请注意,当您在三个参数设置之间切换时,相机的移动方式会有所不同。
这需要启用Java的启用WebGL的浏览器。
Conclusion
我们刚刚探讨了参数化相机外部状态的三种不同方式。 您更喜欢使用哪个参数设置取决于您的应用程序。 如果您正在编写Wolfenstein风格的FPS,您可能会喜欢以世界为中心的参数化,因为沿(t_z)的移动始终对应于向前走。 或者,您可能通过场景中的航路点对摄像机进行插值,在这种情况下,首选以摄像机为中心的参数化,因为您可以直接指定摄像机的位置。 如果不确定自己喜欢哪种方法,请使用上面的工具并确定哪种方法最自然。
下次当我们探索内在矩阵时,请加入我们,我们将了解为什么缩放相机永远无法显示场景的隐藏部分。 回头见!



