剖析相机矩阵,第3部分:内在矩阵
今天,我们将在“剖析相机矩阵”三部曲的第三章和最后一章中研究内在相机矩阵。 在第一篇文章中,我们学习了如何将完整的相机矩阵拆分为内部矩阵和外部矩阵,以及如何正确处理此过程中出现的歧义。 第二篇文章更详细地研究了外部矩阵,研究了其3D旋转和平移的几种不同解释。 今天,我们将对内在矩阵进行相同的处理,研究两种等效的解释:作为虚拟相机几何形状的描述以及一系列简单的2D变换。 之后,您将看到一个交互式演示,其中演示了两种解释。

如果您对深入研究该理论不感兴趣,而只想将内在矩阵与OpenGL一起使用,请查看文章《不带glFrustum的OpenGL中的校准相机》和《校准相机和gluPerspective》。
所有这些文章都是“透视相机,互动之旅”系列的一部分。 要阅读该系列中的其他条目,请转至目录。
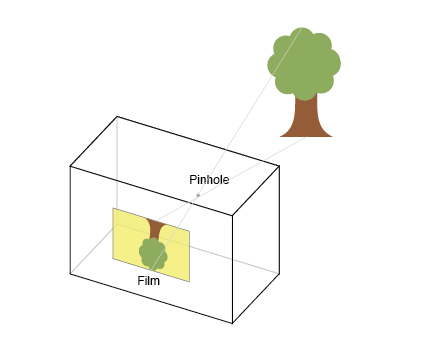
针孔相机(The Pinhole Camera)
固有矩阵(intrinsic matrix)将3D相机坐标转换为2D均匀图像坐标。 该透视投影是由理想的针孔相机建模的,如下图所示。
内在矩阵由Hartley和Zisserman参数化为
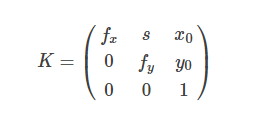
每个固有参数都描述了相机的几何特性。 让我们详细研究每个属性。
焦距,fx,fy
焦距是针孔与胶片(又称为像面)之间的距离。 由于某些原因,我们将在后面讨论,焦距以像素为单位。 在真正的针孔相机中,fx和fy具有相同的值,如下面的f所示。
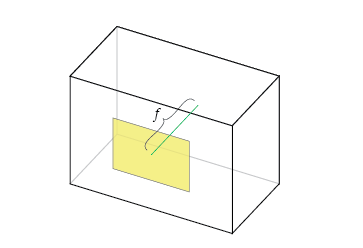
实际上,由于多种原因,fx和fy可能会有所不同:
- 数码相机传感器中的缺陷。
- 图像在后期处理中缩放比例不一致。
- 相机镜头会造成意外的失真。
- 相机采用变形格式(anamorphic format,),镜头将宽屏场景压缩为标准尺寸的传感器。
- 相机校准错误。
在所有这些情况下,所得图像均具有非正方形像素(non-square pixels)。
具有两个不同的焦距并不是很直观,因此某些文本(例如Forsyth和Ponce)使用单个焦距和“长宽比”来描述与完美正方形像素的偏差量。 这样的参数化很好地将相机的几何形状(即焦距i.e. focal length)与失真distortion(纵横比aspect ratio)分开。
主点偏移(Principal Point Offset),x0,y0
相机的“主轴”是垂直于穿过针孔的像平面的线。 其与像平面的迭代称为“主要点”,如下所示。
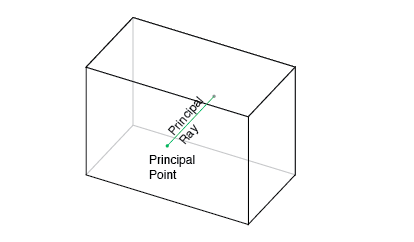
“主要点偏移”是主要点相对于胶片原点的位置。 确切的定义取决于将哪个约定用于原点的位置。 下图假定它位于电影的左下角。
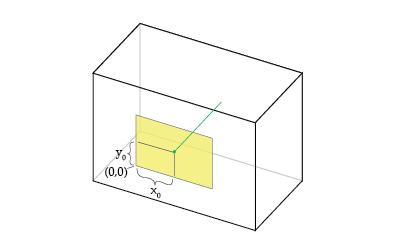
x0增大将针孔向右移动:
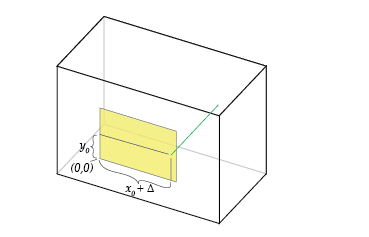
这等效于将胶片向左移动并保持针孔不变。
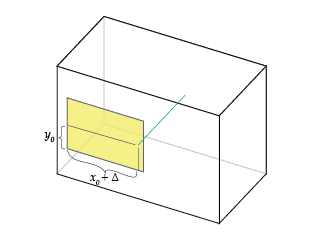
请注意,相机周围的盒子无关紧要,只有针孔相对于胶卷的位置很重要。
轴偏斜,s (Axis Skew, s)
轴偏斜会导致投影图像中的剪切变形。 据我所知,真正的针孔相机没有任何类似的轴偏斜,但显然一些数字化过程会导致非零偏斜。 我们将在稍后讨论偏斜。
其他几何特性(Other Geometric Properties)
焦距和主点偏移等于胶片相对于针孔的简单平移。 还必须有其他方法来变换相机,对不对? 旋转或缩放胶片怎么办?
围绕针孔旋转胶片等同于旋转相机本身,由外部矩阵处理。 绕任何其他固定点x旋转胶片等效于绕针孔P旋转,然后平移(x-P)。
那么缩放呢? 显然,将所有相机尺寸(胶片大小和焦距)加倍不会对捕获的场景产生影响。 相反,如果将胶片尺寸而不是焦距加倍,则相当于将两者都加倍(无操作),然后将焦距减半。 因此,明确地表示电影的比例是多余的。 它是由焦距捕获的。
焦距-从像素到世界单位(Focal Length - From Pixels to World Units)
对摄像机缩放比例的讨论表明,有无限数量的 pinhole camera可以产生相同的图像。 固有矩阵(intrinsic matrix)仅与相机坐标和图像坐标之间的关系有关,因此相机的绝对尺寸无关紧要。 将像素单位用于焦距和主点偏移可以使我们表示相机的相对尺寸,即胶卷相对于其像素尺寸的位置。
另一种说法是,固有的摄像机变换对于摄像机几何形状的均匀缩放是不变的。 通过以像素为单位表示尺寸,我们自然可以捕获这种不变性。
如果您知道至少一个摄像机的世界单位尺寸,则可以使用类似的三角形将像素单位转换为世界单位(例如,毫米)。 例如,如果您知道相机的胶卷(或数字传感器)的宽度W以毫米为单位,并且图像宽度以像素为单位w,则可以使用以下方法将焦距fx转换为世界单位:
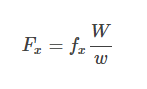
可以使用类似的公式将其他参数fy,x0和y0转换为其对应的世界单位Fy,X0和Y0:
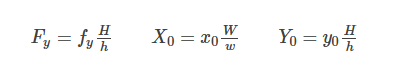
相机视锥-简化针孔相机(The Camera Frustum - A Pinhole Camera Made Simple)
正如我们前面讨论的,针孔和胶片的排列只是物质,所以相机周围的物理盒子是无关紧要的。 因此,许多关于相机几何形状的讨论都使用了一种更简单的视觉表示:相机视锥。
相机的可视区域是金字塔形的,有时也称为“可视范围”。 让我们向场景中添加一些3D球体,展示它们如何落入可见性圆锥体中并创建图像

由于相机的“盒子”无关紧要,我们将其删除。 另外,请注意,电影的图像描绘了现实的镜像版本。 为了解决这个问题,我们将使用“虚拟图像”代替电影本身。 虚拟图像与胶片图像具有相同的属性,但是与真实图像不同,虚拟图像出现在相机的前面,并且投影图像未翻转。

请注意,虚拟图像平面的位置和大小是任意的-只要将其与针孔的距离加倍,我们就可以将其大小加倍。
删除真实图像后,剩下的是针孔相机的“查看视锥”表示。
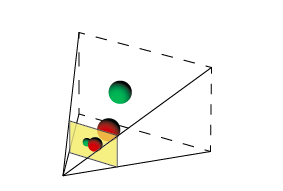
针孔已被可见性圆锥体的尖端代替,并且影片现在由虚像平面表示。 稍后,我们将在演示中使用此表示形式。
固有参数作为2D转换(Intrinsic parameters as 2D transformations)
在前面的部分中,我们将传入的3矢量解释为3D图像坐标,然后将其转换为同质2D图像坐标。 或者,我们可以将这3个向量解释为2D同构坐标,将其转换为一组新的2D点。 这使我们对内在矩阵有了新的认识:一系列2D仿射变换。
我们可以将本征矩阵分解为剪切,缩放和平移变换的序列,分别对应于轴偏斜(axis skew),焦距(focal length)和主点偏移(principal point offset):
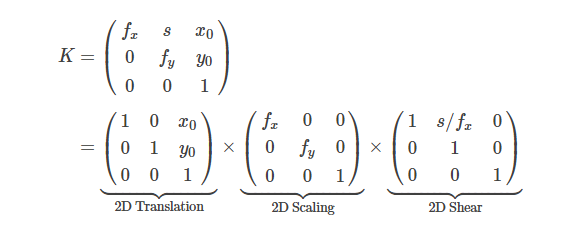
等效分解在缩放后放置剪切:
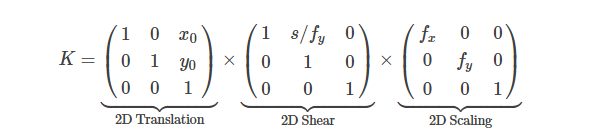
这种解释很好地将外部参数和内部参数分别有效地分为3D和2D领域。 它还强调,固有的相机变换发生在投影后。 一个显着的结果是,固有参数不会影响可见性( intrinsic parameters cannot affect visibility )-被遮挡的对象无法通过图像空间中的简单2D变换来显示。
Demo
下面的演示说明了对内在矩阵的两种解释。 左侧是“相机几何形状”的解释。 请注意,随着x0和y0的调整,针孔如何相对于像平面移动。
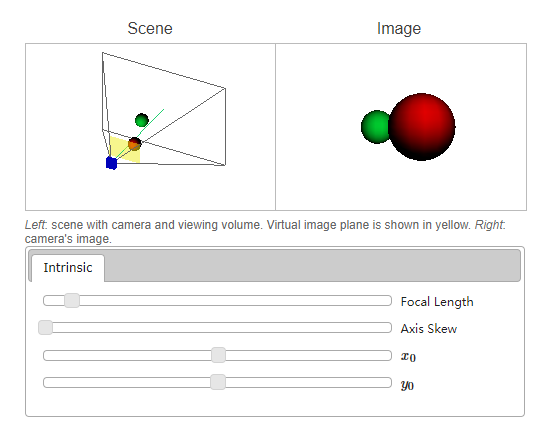
剖析相机矩阵,摘要(Dissecting the Camera Matrix, A Summary)
在本系列文章的过程中,我们已经了解了如何分解
- 完整的相机矩阵分为内在和外在矩阵,
- 将外部矩阵转换为3D旋转,然后进行平移,以及
- 将固有矩阵转换为三个基本的2D转换。
我们在下面总结此完整分解。
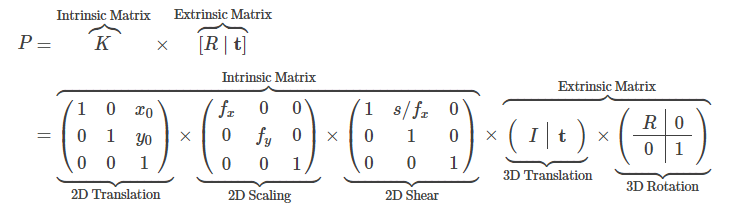
要查看所有这些转换的实际效果,请转到我的“透视相机玩具”页面,以获取全透视相机的交互式演示。
您还有其他解释固有相机矩阵的方法吗? 发表评论或给我留言!
下次,我们将展示如何准备经过校准的相机以生成立体图像对。 回头见!



