非线性最小二乘问题的方法
1.简介和定义............................... 1
2.设计方法.................................................. 5
2.1.最陡下降法. ..................... 7
2.2.牛顿法. ........................................................ 8
2.3.线搜索...................................................................................... 9
2.4.信赖域和阻尼方法........................................ 11
3.非线性最小二乘问题........................................ 17
3.1.高斯-牛顿法........................................ 20
3.2. Levenberg–Marquardt方法........................................ .24
3.3.鲍威尔的狗腿法........................................ 29
3.4.混合方法：LM和拟牛顿.........................................34
3.5. L–M方法的割线形式........................................ 40
3.6.狗腿法的一个正割版本........................................ 45
3.7.最后的评论........................................ 47
附录........................................ 50
参考资料........................................ 55
索引........................................57
1.引言和定义
在本手册中，我们考虑以下问题
范例1.1. 最小二乘问题的重要来源是数据拟合。 例如，请考虑以下所示的数据点（t1，y1），...，（tm，ym）
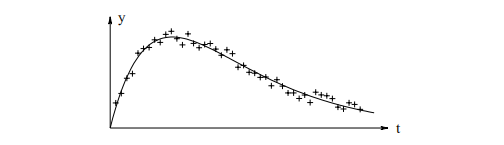
图1.1 数据点{（ti，yi）}（用+标记）和模型M（x，t）（用实线标记）
此外，我们给出了拟合模型，
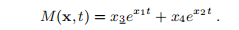
模型取决于参数x = [x1，x2，x3，x4]T。 我们假设存在一个x†，因此
{εi}是数据坐标上的（测量）误差，假定像“白噪声”一样。
对于x的任何选择，我们都可以计算残差
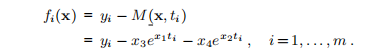
对于最小二乘拟合，将参数确定为残差平方和的最小值x∗。 可以看出这是定义1.1中n = 4形式的问题。在图1.1中用实线显示了M（x∗，t）的图。
最小二乘问题是更常见问题的一个特殊变体：给定函数F：IRn→IR，找到参数F，该参数给出该所谓的目标函数或成本函数的最小值。
定义1.2 全局最小化器
一般而言，这个问题很难解决，我们仅介绍解决以下简单问题的方法：找到F的局部极小值，这是一个自变量矢量，在某个区域内给出了F的最小值，其大小由δ给出，其中 δ是一个小的正数。
定义1.3 本地最小化器
在本介绍的其余部分中，我们将讨论优化中的一些基本概念，第2章简要介绍了为一般成本函数找到局部最小化器的方法。 有关更多详细信息，请参阅Frandsen等人（2004年）。 在第3章中，我们提供了针对最小平方问题专门调整的方法。
我们假设成本函数F是可微的且非常平滑，以至于随后的泰勒展开式是有效的，2
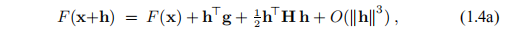
其中g是梯度，
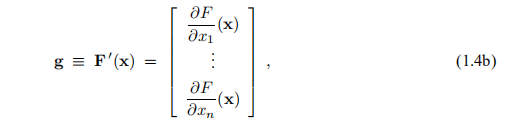
H是Hessian(在数学中，Hessian矩阵或Hessian是标量值函数或标量场的二阶偏导数的平方矩阵。 它描述了许多变量的函数的局部曲率。)
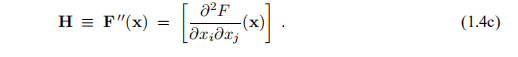
如果x∗是局部极小值并且||h||足够小，则我们找不到具有较小F值的点x∗ + h。 将此观察值与（1.4a）结合，我们得到
定理1.5 局部最小化器的必要条件。
如果x∗是局部极小值，则
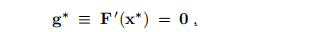
对于满足必要条件的参数，我们使用特殊名称：
定义1.6 固定点。 如果
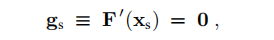
那么xs被认为是F的固定点。
因此，局部最小化器也是固定点，但是局部最大化器也是如此。 既不是局部最大化器也不是局部最小化器的固定点称为鞍点。 为了确定给定的固定点是否是局部极小值，我们需要在泰勒级数（1.4a）中包括二阶项。 插入xs我们看到
根据Hessian的定义（1.4c），可以得出任何H是对称矩阵。 如果我们要求Hs是正定的，则其特征值大于某个值δ> 0（请参阅附录A），并且
这表明，对于
足够小的（1.7）右侧的第三项将由第二项占主导。 这个词是肯定的，所以我们得到
定理1.8 局部最小化器的充分条件
假设xs是一个固定点，并且F''(xs)是正定的。 那么xs是一个局部最小化器。
如果Hs是负定数，则xs是局部最大化器。 如果Hs是不确定的（即，它同时具有正和负特征值），则xs是一个鞍点。
2.设计方法
所有用于非线性优化的方法都是迭代的：从起点x0开始，该方法会产生一系列向量x1，x2，...，（希望地）收敛为给定函数的局部极小值x∗，请参见定义1.3大多数方法都有强制降低条件的措施
这会阻止收敛到最大化器，也使收敛到鞍点的可能性降低。 如果给定的函数具有多个最小化器，则结果将取决于起点x0。 我们不知道会找到哪个最小化器。 它不一定是最接近x0的最小化器。
在许多情况下，该方法产生的向量在两个明显不同的阶段收敛到最小化器。 当x0远离解时，我们希望该方法产生迭代，并朝x∗稳定地移动。 在迭代的这个“全局阶段”，如果除了第一步之外的错误没有增加，我们就感到满意，即
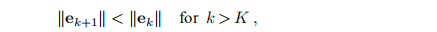
其中ek表示当前错误，
在迭代的最后阶段，xk接近x ∗，我们想要更快的收敛速度。 我们区分
线性收敛（Linear convergence）：
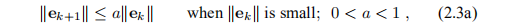
二次收敛（Quadratic convergence）：
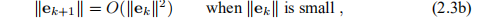
超线性收敛（Superlinear convergence）：
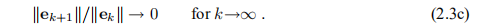
本讲义中介绍的方法是下降方法，在迭代的每个步骤中都满足下降条件（2.1）当前迭代的第一步在于
1.找到下降方向hd（如下所述），然后
2.找到一个步长，使F值大大降低。
考虑F值沿着从x开始并沿h方向的一半线的变化。 从泰勒展开式（1.4a）中，我们看到
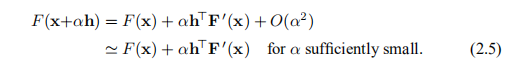
我们说，如果F(x +αh)是α在α= 0时的递减函数，则h是下降方向。这导致以下定义。
定义2.6. 下降方向
如果不存在这样的h，则F'(x)= 0，这表明x在这种情况下是固定的。 否则，我们必须选择α，即在hd给出的方向上距x应该走多远，以便使目标函数的值减小。 一种方法是找到（近似）
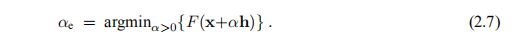
该过程称为行搜索，将在第2.3节中讨论。 但是，首先，我们将介绍两种计算下降方向的方法。
2.1.The Steepest Descent method最陡下降法
从（2.5）可以看出，当我们以正α执行步长αh时，函数值的相对增益就可以满足
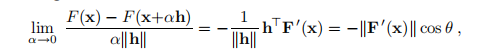
其中θ是向量h和F'(x)之间的夹角。 这表明如果θ=π，即使用以下公式给出的最陡下降方向hsd，我们将获得最大增益率：
基于（2.8）的方法（即算法2.4中的hd = hsd）被称为最速下降法或梯度法。 下降方向的选择（局部）是“最佳”，我们可以将其与精确的线搜索（2.7）结合起来。 这样的方法会收敛，但是最终收敛是线性的，并且通常很慢。 Frandsen等人（2004年）中的示例表明，具有精确线搜索和有限计算机精度的最速下降方法如何无法找到二次多项式的极小值。 但是，对于许多问题，该方法在迭代过程的初始阶段具有相当好的性能。
诸如此类的考虑导致了所谓的混合方法，顾名思义，该方法基于两种不同的方法。 一种在初始阶段很好，例如梯度法，另一种在最后阶段很好的方法，例如牛顿法。 请参阅下一节。 混合方法的主要问题是在适当时在两种方法之间切换的机制。
2.2. 牛顿法 Newton’s Method
我们可以从x*是一个固定点的条件中得出这种方法。 根据定义1.6，它满足F'(x*)=0。这是一个非线性方程组，根据泰勒展开式
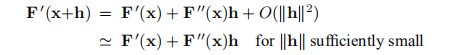
我们推导出牛顿的方法：找到hn作为解
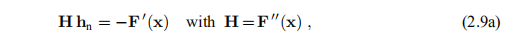
并计算下一个迭代
假设H是正定的，则它是非奇异的（暗示（2.9a）具有唯一解），并且对于所有非零u，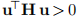
。 因此，通过在（2.9a）的两边乘以h> n，我们得到
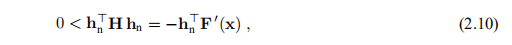
表明hn是下降方向：它满足定义2.6中的条件。
牛顿的方法在迭代的最后阶段非常好，其中x接近x ∗。 可以证明（参见Frandsen等人（2004）），如果解中的Hessian是正定的（满足定理1.8中的充分条件），并且我们在x∗周围的区域内的位置是F''( x)是正定的，则我们得到二次收敛（在（2.3）中定义）。 另一方面，如果x处在F''(x)到处都是负定且存在固定点的区域，则基本牛顿法（2.9）会（正交）收敛于该固定点，即 最大化器。 我们可以通过要求所有步骤都沿下降方向来避免这种情况。
我们可以基于牛顿法和最速下降法建立一种混合方法。 根据（2.10），如果F00（x）是正定的，则牛顿阶跃保证为下坡，因此该混合算法的中心部分的草图可以为
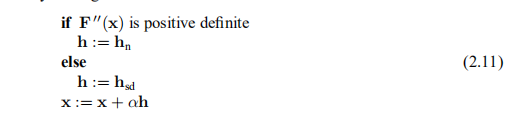
在此，hsd是最陡的下降方向，并且通过线搜索找到α； 请参阅第2.3节。 Cholesky方法（请参阅附录A）是检查矩阵的正定性的一个很好的工具，该方法成功后也可用于求解所讨论的线性系统。 因此，确定性检查几乎是免费的。
在第2.4节中，我们介绍了一些方法，其中搜索方向hd和步长α的计算是同时进行的，并给出了（2.11）的版本，而没有行搜索。 这种混合方法可能非常有效，但是几乎从未使用过。 原因是它们需要F''(x)的实现，对于复杂的应用程序问题，这是不可用的。 取而代之的是，我们可以根据逐渐接近H* = F''(x*)的一系列矩阵使用所谓的拟牛顿法。 在第3.4节中，我们介绍了这种方法。 另请参阅Frandsen等人（2004年）的第5章。
2.3. 线搜索Line Search
给定点x和下降方向h。 下一个迭代步骤是从x向h方向移动。 为了找出移动的距离，我们研究了给定函数沿x沿h方向从x的一半线的变化，
2.1（α）的行为示例如图2.1所示。
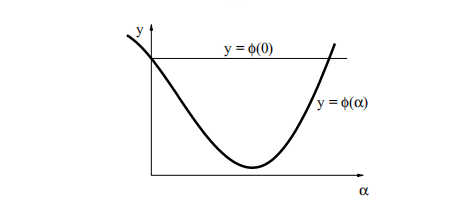
图2.1. 成本函数沿搜索线的变化。
我们h是下降的方向，可以确保
表示如果α足够小，我们满足下降条件（2.1），它等于
通常，我们会对α进行初步猜测，例如，使用牛顿法，α= 1。 图2.1说明了可能出现的三种不同情况
1)更准确地说：local的最小局部最小值。 如果我们将α增加到超过图2.1中所示的间隔，则很可能我们接近F的另一个局部最小值。
精确线搜索是产生一系列α1，α2...的迭代过程。 目的是找到在（2.7）中定义的真正的最小化子αe，并且算法在迭代的αs满足时停止
其中τ是一个小的正数。 在迭代中，我们可以基于计算的值对ϕ（α）的变化使用近似值。
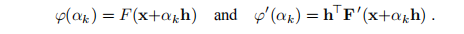
有关详细信息，请参见Frandsen等人（2004年）的第2.5 – 2.6节。
精确的行搜索会浪费大量的计算时间：当x远离x ∗时，搜索方向h可能会偏离x ∗ −x方向，因此无需非常精确地找到the的真实最小值。 这就是所谓的“软线搜索”的背景，如果它不属于上面列出的1◦或2◦类别，则我们接受该值。 我们使用降级条件（2.1）的严格版本，即
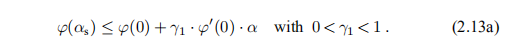
这确保了我们不会处于情况2◦中。 情况1◦对应于点（α，ϕ（α））太接近起始切线，我们补充了条件
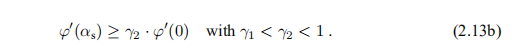
如果对α的初始猜测满足这两个标准，那么我们将其视为αs。 否则，我们必须按照草图进行迭代以进行精确的线搜索。 有关详细信息，请参见Frandsen等人（2004年）的2.5节。
2.4. 信任区域和阻尼方法Trust Region and Damped Methods
假设我们在当前迭代x的附近有一个F行为的模型L，
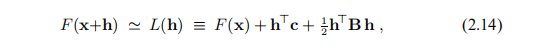
其中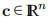
和矩阵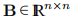
是对称的。 本节的基本思想可以推广到模型的其他形式，但是在本手册中，我们只需要（2.14）中给出的L形式。 通常，模型是F围绕x的二阶泰勒展开，就像（1.4a）右侧的前三个项或L（h）可能是该展开的近似值。 通常，只有当h足够小时，这种模型才是好的。 我们将在确定步长h的过程中引入包括这方面的两种方法，步长h是下降方向，可以在算法2.4中与α= 1一起使用。
在信任区域方法中，我们假设我们知道一个正数∆，以使模型在半径为∆的球（以x为中心）内足够精确，并将步长确定为
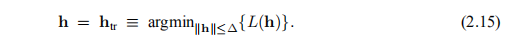
在阻尼方法中，该步骤确定为
其中阻尼参数µ≥0。认为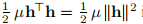
会惩罚较大的步长
基于这些方法之一的算法2.4的中心部分具有以下形式
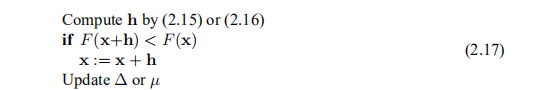
如果步长h满足下降条件（2.1），则这对应于α= 1。 否则，α= 0，即我们不动2）但是，我们不会陷入x的困境（除非x = x ∗）：通过对∆或µ进行适当的修改，我们的目标是在下一个迭代步骤中获得更好的运气。
2)这些方法有多种版本，其中包括适当的线搜索以查找具有较小F值的点x +αh，并且在线搜索过程中收集的信息用于∆或µ的更新。 对于许多问题，此类版本使用较少的迭代步骤，但使用更多的函数值累积量。
由于对于h足够小，L（h）被认为是F（x + h）的良好近似值，因此步失败的原因是h太大，应将其减小。 此外，如果接受该步骤，则有可能使用新迭代中的较大步骤，从而减少我们达到x*之前所需的步骤数。
具有计算步骤的模型的质量可以通过所谓的增益比来评估
即功能值实际减少与预测减少之间的比率。 通过构造，分母为正，如果台阶不是下坡，则分子为负–太大，应减小。 使用信任区域方法，我们通过半径∆的大小监视步长。 以下更新策略被广泛使用，
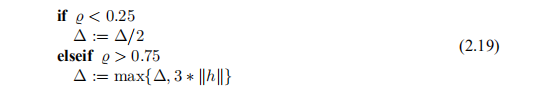
因此，如果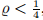
，我们决定使用较小的步长，而％> 34表示可能使用较大的步长。 信任区域算法对阈值0.25和0.75，除数p1 = 2或因数p2 = 3的微小变化不敏感，但是选择数字p1和p2以使Δ值不发生振荡很重要。
在阻尼方法中，％的较小值表示我们应该增加阻尼系数，从而增加大步幅的代价。 ％的大值表示对于计算出的h，L（h）非常接近F（x + h），并且可以减小阻尼。 以下是一种广泛使用的策略，它与（2.19）类似，最初是由Marquardt（1963）提出的，
同样，该方法对阈值0.25和0.75或数字p1 = 2和p2 = 3的微小变化不敏感，但重要的是选择数字p1和p2，以使µ值不会振荡。 经验表明，跨越阈值0.25和0.75的不连续变化会引起“波动”（如第27页的示例3.7所示），这会减慢收敛速度，我们在Nielsen（1999）中证明，以下策略在总体上胜过 （2.20），
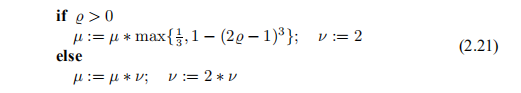
将因数ν初始化为ν=2。请注意，一系列连续的故障导致µ值迅速增加。 这两个更新公式如下所示。
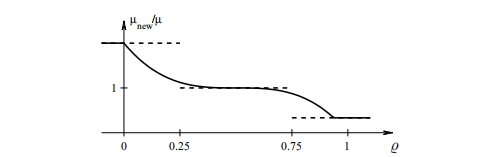
图2.2. Mar的策略（2.20）（虚线）用ν= 2（实线）将µ更新为（2.21）。
2.4.1. 步骤计算Computation of the step.
在阻尼方法中，该步被计算为函数的固定点
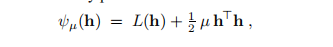
这意味着hdm是解决
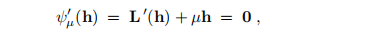
从（2.14）中L（h）的定义中我们看到，这等效于
我是单位矩阵 如果µ足够大，则对称矩阵B + µI是正定的（如附录A所示），然后从定理1.8可以看出hdm是L的极小值
示例2.1 在阻尼牛顿法中，模型L(h)由c = F'(x)和B = F''(x）给出，而（2.22）的形式为
即在接近最陡下降方向的方向上的短步。 另一方面，如果μ很小，则hdn接近牛顿步距hn。 因此，我们可以认为阻尼牛顿法是最速下降法和牛顿法的混合体。
我们将在第3.2节中返回阻尼方法。
在信任区域方法中，步骤htr是约束优化问题的解决方案，
对此问题进行任何详细讨论都超出了本手册的范围（请参阅Madsen等人（2004年）或Nocedal and Wright（1999年）中的4.1节。我们只想提及一些特性。
如果（2.14）中的矩阵B是正定的，则L的无约束最小化子为
如果该值足够小（如果满足hT h≤∆2），则这是所需的步骤htr。 否则，约束将处于活动状态，并且问题更加复杂。 使用与第11页类似的论点，我们可以看到我们不必计算（2.23）的真实解，并且在第3.3和3.4节中，我们提供了两种计算htr近似值的方法。
最后，在B为正定的情况下，我们在阻尼方法和信任区域方法之间存在两个相似之处：如果无约束极小子在信任区域之外，则可以证明（Madsen等人（2004年，定理2.11 ））存在一个λ> 0使得
通过对该方程重新排序并将其与（2.22）进行比较，我们可以看到htr与使用阻尼参数µ =λ计算的阻尼阶跃hdm相同。 另一方面，还可以证明（Frandsen等人（2004年）中的定理5.11），如果我们针对给定的µ≥0计算hdm，则
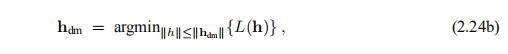
即hdm等于对应于信任区域半径∆ = ||hdm||的htr。 因此，这两种方法密切相关，但是对于给出相同步骤的∆值和µ值之间的联系，没有简单的公式。
3. 非线性最小二乘问题NON-LINEAR LEAST SQUARES PROBLEMS
在本讲义的其余部分，我们将讨论非线性最小二乘问题的方法。 给定一个向量函数f：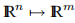
，m≥n。 我们要最小化||f(x)||或等效地找到
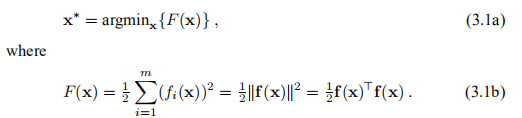
最小二乘问题可以通过一般的优化方法来解决，但我们将介绍更有效的特殊方法。 在许多情况下，即使不需要二阶导数，它们也比线性收敛，有时甚至是二次收敛要好。 在本章方法的描述中，我们将需要F的导数的公式：假设f具有连续的二阶偏导数，我们可以将其泰勒展开式写为
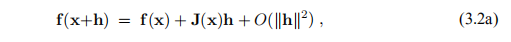
其中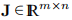
是雅可比行列式。 这是一个矩阵，其中包含功能组件的一阶偏导数，
关于F：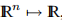
，它来自（3.1b）中的第一个公式，
那1）
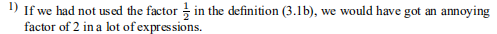
1)如果在定义（3.1b）中未使用因子1/2，则在许多表达式中我们将得到令人讨厌的因子2。
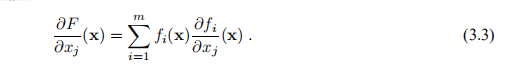
因此，梯度（1.4b）为
我们还需要F的Hessian。从（3.3）可以看出，位置（j，k）的元素是
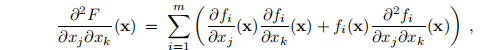
显示
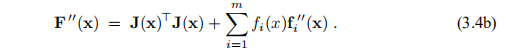
示例3.1 （3.1）的最简单情况是f（x）的形式为
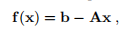
给出了向量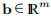
和矩阵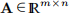
。 我们说这是一个线性最小二乘问题。 在这种情况下，对于所有x，J（x）= −A，从（3.4a）中我们看到
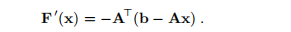
对于确定为所谓正态方程的解的x∗，该值为零。
问题可以以以下形式写
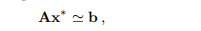
或者我们可以通过正交变换来解决它：找到一个正交矩阵Q使得
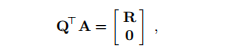
其中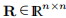
是上三角。 通过系统中的反向替换找到解决方案2）
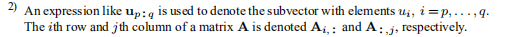
2)像up：q这样的表达式用于表示元素ui为i = p，的子向量... ，q. 矩阵A的第i行和第j列分别表示为Ai ,:和A：,J,
该方法比通过正态方程的解决方案更准确
在MATLAB中，假定数组A和b分别包含矩阵A和向量b。 然后，命令A \ b返回通过正交变换计算的最小二乘解。
正如手册标题所暗示的，我们假定f是非线性的，因此将不详细讨论线性问题。 我们参考Madsen和Nielsen（2002）中的第2章，或Golub和Van Loan（1996）中的5.2节。
示例3.2 在示例1.1中，我们看到了由数据拟合引起的非线性最小二乘问题。 另一个应用是解决非线性方程组，
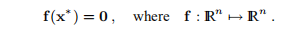
我们可以使用牛顿-拉夫森（Newton-Raphson）的方法：根据初始猜测x0，通过以下算法计算x1，x2，...，该算法基于寻找h使得f（x + h）= 0并忽略术语O（||h||2 ）在（3.2a）中，
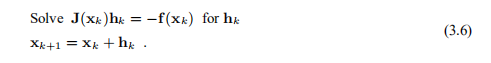
这里，雅可比定律J由（3.2b）给出。 如果J（x ∗）是非奇异的，则该方法具有二次最终收敛性，即，如果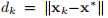
小，则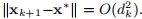
但是，如果xk远离x ∗，那么我们就有可能走得更远。
我们可以重新构造问题，使其能够使用本章将要介绍的所有“工具”：（3.6）的解决方案是由（3.1）定义的函数F的全局最小值，
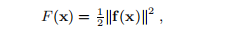
因为如果f（x）= 0，则F(x*)= 0且F（x）>0。例如，我们可以将（3.6）中的近似解的更新替换为
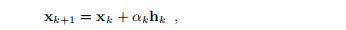
其中，通过对函数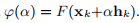
进行线搜索来找到αk。 作为一个具体示例，我们将考虑以下问题，该问题取自Powell（1970），
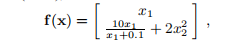
x ∗ = 0是唯一的解决方案。 雅可比式是
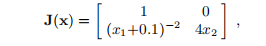
在解决方案上是唯一的。
如果我们取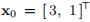
并使用上述算法进行精确行搜索，则迭代收敛到
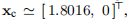，这不是解决方案。 另一方面，很容易看出，算法（3.6）给出的迭代为
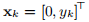，其中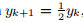
，即我们对解具有线性收敛性。 在许多示例中，我们将返回到该问题，以查看不同的方法如何处理它。
3.1. 高斯-牛顿法The Gauss–Newton Method
此方法是我们将在下一部分中介绍的非常有效的方法的基础。 它基于向量函数各成分的已实现一阶导数。 在特殊情况下，它可以给出二次收敛，就像牛顿法进行一般优化一样，请参见Frandsen等人（2004年）。
高斯-牛顿法基于x附近的f的线性近似（f的线性模型）：对于小||h||，我们从泰勒展开式（3.2）中得出：
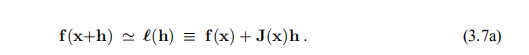
将其插入F的定义（3.1）中，我们看到
（其中f = f（x）且J = J（x））。 高斯-牛顿步长hgn将L（h）最小化，
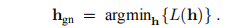
可以很容易地看出L的梯度和Hessian为
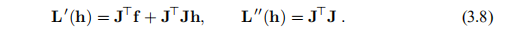
与（3.4a）的比较表明L'(0)= F'(x)。 此外，我们看到矩阵L''(h)独立于h。 它是对称的，并且如果J具有最高秩，即，如果列是线性独立的，则L''（h）也是正定的，请参阅附录A。这意味着L(h)具有唯一的极小值，可以通过求解来找到
这是F的下降方向，因为
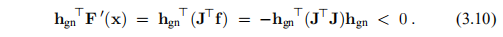
因此，我们可以在算法2.4中将hgn用于hd。 典型的步骤是
通过行搜索找到α。 经典的高斯-牛顿法在所有步骤中都使用α= 1。 可以证明，采用线搜索的方法具有瓜尔特事先收敛性，条件是
a）{x | F(x)≤F(x0)}有界，并且
b）雅可比J(x)在所有步骤中都具有最高等级
在第二章中，我们看到牛顿的优化方法具有二次收敛性。 高斯-牛顿法通常不是这种情况。
为此，我们比较了两种方法中使用的搜索方向，
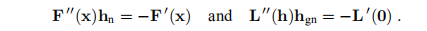
我们已经在（3.8）处指出两个右侧相同，但是从（3.4b）和（3.8）中我们看到系数矩阵不同：
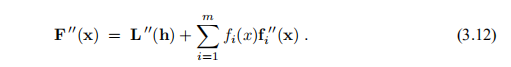
因此，如果f(x∗)= 0，则x的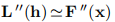
接近x*，并且我们也用高斯-牛顿法得到二次收敛。 如果函数{fi}的曲率小或
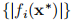小，我们可以期望超线性收敛，但是总的来说我们必须期望线性收敛。 值得注意的是，F(x∗)的值控制着收敛速度。
示例3.3 考虑n = 1的简单问题，m = 2由
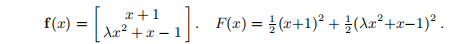
它遵循
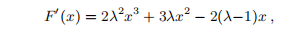
所以x = 0是F的固定点。现在，
这表明如果λ<1，则F''(0)> 0，因此x = 0是局部最小化器-实际上，它是全局最小化器。
雅可比式是
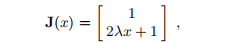
xk的经典高斯-牛顿法给出
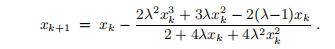
现在，如果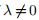
且xk接近零，则
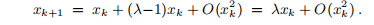
因此，如果|λ| <1，我们有线性收敛。 如果λ<-1，则经典高斯牛顿法无法找到最小化器。 例如，当λ= − 2且x0 = 0.1时，我们得到了迭代器看似混乱的行为，
最后，如果λ= 0，则
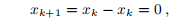
即，我们一步找到解决方案。 原因是在这种情况下，f是线性函数。
示例3.4 对于示例1.1中的数据拟合问题，雅可比矩阵的第i行为
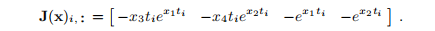
如果问题是一致的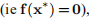
，那么只要x1∗ 1与x2∗ 显着不同，则带线搜索的高斯-牛顿法将具有二次最终收敛性。 如果
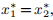，则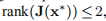
，并且高斯牛顿法失败。
如果一个或多个测量误差较大，则f（x ∗）的分量较大，这可能会降低收敛速度。
在MATLAB中，我们可以提供一个非常紧凑的函数来计算f和J：假设x保持当前迭代，并且m×2数组ty保持数据点的坐标。 以下函数返回分别包含f（x）和J（x）的f和J。
示例3.5 考虑示例3.2中的问题，其中f（x ∗）= 0，其中f：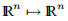
。 如果我们使用Newton-Raphson的方法来解决此问题，则典型的迭代步骤是
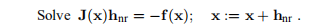
用于最小化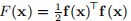
的高斯-牛顿法具有典型步骤
注意，J（x）是一个方矩阵，并且我们假定它不是奇异的。 然后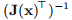
存在，并由此得出hgn = hnr。 因此，将高斯-牛顿法应用于例3.2中的鲍威尔问题时，将遇到与该例中的牛顿-拉夫森法相同的麻烦
这些示例表明，无论是否进行线搜索，高斯-牛顿法都可能会失败。 尽管如此，它在许多应用中仍具有相当好的性能，尽管通常它仅具有线性收敛性，而与牛顿方法中实现二次导数的二次收敛性相反。
在3.2和3.3节中，我们给出了两种具有较高全局性能的方法，而在3.4节中，我们对第一种方法进行了修改，以实现最终的超线性收敛。
3.2. The Levenberg–Marquardt Method
Levenberg（1944）和后来的Marquardt（1963）建议使用阻尼高斯-牛顿法，请参见第2.4节。 通过对（3.9）的以下修改来定义步骤hlm，
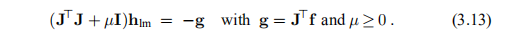
在此，J ＝ J（x），f ＝ f（x）。 阻尼参数µ有几个作用：
a）对于所有μ> 0，系数矩阵为正定的，这可确保hlm为下降方向，比照（3.10）。
b）对于较大的µ，我们得到
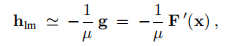
即沿最陡的下降方向的一小步。 如果当前的迭代距离解还很远，那么这很好。
c）如果µ很小，则当x接近x ∗时，hlm'hgn是迭代最后阶段的一个好步骤。 如果F（x∗）= 0（或很小），那么我们可以（几乎）获得二次最终收敛。
因此，阻尼参数会影响步长的方向和大小，从而导致我们做出一种无需特定线搜索的方法。 初始µ值的选择应与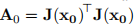
中元素的大小有关，例如
其中τ由用户选择3）在迭代过程中，μ的大小可以按照2.4节所述进行更新。 更新由增益比控制
3）该算法对τ的选择不是很敏感，但是根据经验，如果x0被认为是对x ∗的良好近似，则应使用较小的值，例如τ= 10-6。 否则，使用τ= 10-3甚至τ= 1。
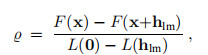
分母是线性模型（3.7b）预测的增益，
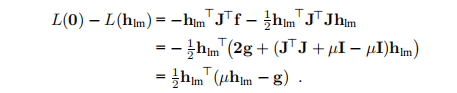
注意，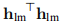
和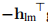
均为正，因此
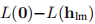保证为正。
％的大值表示L（hlm）是F（x + hlm）的良好近似值，我们可以减小µ，以便下一个Levenberg-Marquardt步骤更接近于Gauss-Newton步骤。 如果％小（甚至可能为负），则L（hlm）的近似值很差，我们应该增加µ的双重目的是接近最陡的下降方向并减小步长。 这些目标可以通过不同的方式实现，请参见第14页和下面的示例3.7。
该算法的停止标准应反映出，在全局最小化器中，我们有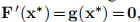
，因此我们可以使用
其中ε1是用户选择的较小的正数。 另一个相关标准是，如果x的变化很小，则停止；
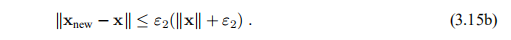
该表达式给出了从渐进变化的相对步长ε2（当|x|大时）到绝对步长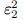
（如果x接近0）的变化。最后，像在所有迭代过程中一样，我们需要防范无限循环的保护措施，
ε2和kmax也由用户选择。
最后两个标准生效，例如，如果ε1选择得太小以至于舍入误差的影响会很大。 通常，这将使F的实际增益与线性模型预测的增益（3.7b）之间的符合性差，从而导致µ在每个步骤中都增大。 增大μ的策略（2.21）表示在这种情况下，μ增长很快，导致khlmk小，并且该过程将被（3.15b）停止。
该算法总结如下。
示例3.6 通过比较（3.9）和正规方程（3.5），我们可以看到hgn只是线性问题的最小二乘解
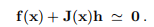
同样，L-M方程（3.13）是线性问题的正规方程
如示例3.1所述，通过正交变换可以找到最准确的解决方案。 但是，解hlm只是迭代过程中的一个步骤，不需要非常精确地计算，并且由于通过正态方程的解是“便宜”的，因此通常使用此方法。
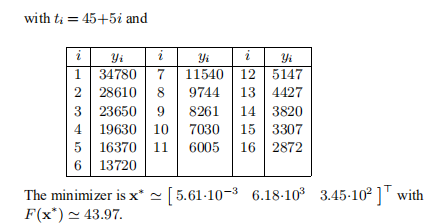
示例3.7 我们已对示例1.1和3.4中的数据拟合问题使用了算法3.16。 图1.1表示x1和x2均为负，并且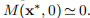
。
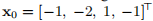满足这些条件。 此外，我们在表达式（3.14）中将τ= 10−3用于µ0，将停止条件由（3.15）给出，其中ε1=ε2= 10−8，kmax =200。该算法在使用x进行62次迭代之后停止 
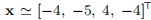。 性能如下所示； 注意对数纵坐标轴。
这个问题不一致，因此我们可以期望线性最终收敛。 最后的7个迭代步骤表明收敛性更好（超线性）。 推论是，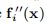
是ti的缓慢变化函数，
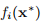具有“随机”符号，因此对（3.12）中的“遗忘项”的贡献几乎抵消了 出来。 这种情况发生在许多数据拟合应用程序中。
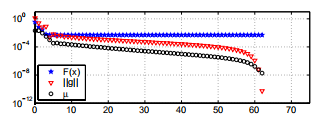
图3.2a。 L-M方法适用于示例1.1中的拟合问题。
为了进行比较，图3.2b显示了使用更新策略（2.20）时的性能。 从步骤5到步骤68，我们看到µ的每个减小都紧随其后增大，并且梯度的范数具有粗糙的行为。 这减慢了收敛速度，但是最后阶段如图3.2a所示。
图3.2b。 使用更新策略的效果（2.20）
示例3.8 图3.3从示例3.2和3.5展示了应用于鲍威尔问题的算法3.16的性能。 起点是x0 = [3，1]>，由（3.14）中的τ= 1给出的µ0，在停止标准（3.15）中，我们使用ε1=ε2= 10-15，kmax = 100。
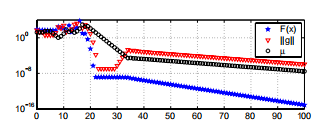
图3.3。 L-M方法适用于鲍威尔的问题。
迭代似乎在步骤22和30之间停止。这是（几乎）奇异雅可比矩阵的影响。 在那之后，似乎出现了线性收敛。 迭代由“保护”在点x = [-3.82e-08，-1.38e-03]T处停止。 与示例3.2相比，这是对x∗ = 0的更好近似，但是我们希望能够做得更好。 参见示例3.10和3.17。
3.3.Powell’s Dog Leg Method鲍威尔的狗腿法
作为Levenberg–Marquardt方法，此方法适用于高斯–牛顿和最陡的下降方向的组合。 现在，可通过信任区域的半径进行显式控制，请参见第2.4节。 鲍威尔的名字与算法有关，因为他提出了如何找到由（2.23）定义的htr的近似值。
给定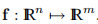
。 在当前迭代x高斯-牛顿步长hgn是线性系统的最小二乘解
可以通过求解正规方程来计算
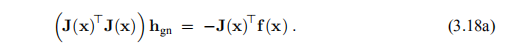
最陡的下降方向为
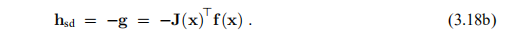
这是一个方向，而不是一个步骤，要了解我们应该走多远，我们看一下线性模型
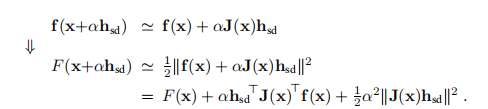
α的这个函数对于
现在，对于从当前点x采取的步骤，我们有两个候选项：a =αhsd和b = hgn。 当信任区域的半径为∆时，鲍威尔建议使用以下策略选择步骤。 该策略的最后一种情况如图3.4所示。
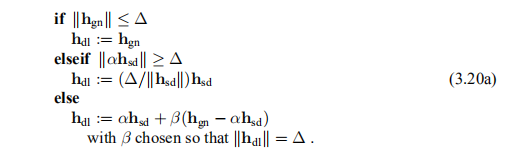
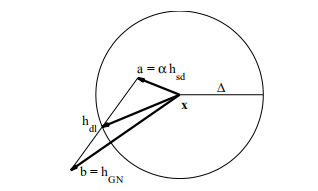
图3.4 信任区域和狗腿步4）
狗腿这个名字取自高尔夫：“狗腿洞”处的球道的形状是从x（发球点）到a的终点到hdl（洞）的终点的线。 鲍威尔是一位敏锐的高尔夫球手！
使用上面定义的a和b，以及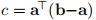
，我们可以写
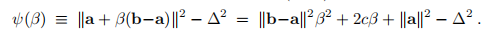
我们为该二阶多项式求根，请注意对于β→−∞，ψ→+∞；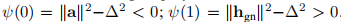
。因此，ψ在] 0，1 [中具有一个负根和一个根。 我们寻找后者，最精确的计算由
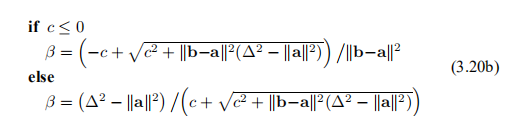
与L-M方法一样，我们可以使用增益比
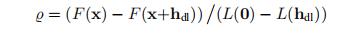
监视迭代。 同样，L是线性模型
在L-M方法中，我们使用％来控制阻尼参数的大小。 在这里，我们使用它来控制信任区域的半径∆。 ％的大值表示线性模型良好。 我们可以增加∆从而采取更长的步骤，并且它们将更接近高斯-牛顿方向。 如果％小（甚至可能为负），则我们减小∆，这意味着更小的步长，更接近最陡的下降方向。 下面我们总结一下算法。
我们有以下几点评论。
1◦初始化。 x0和∆0应由用户提供。
2◦我们使用停止条件（3.15）加上kf（x）k∞≤ε3，反映出在m = n的情况下f（x ∗）= 0，即非线性方程组。
3◦如果m = n，则用“ =”代替“'”，参见（3.6），并且我们不使用绕等式（3.18a）绕行的方法； 参见例3.9。
4◦与（3.20a）中的三种情况相对应，我们可以证明
5◦策略（2.19）用于更新信任区半径。
6◦额外的停止条件。 如果
，则在下一步骤中肯定会满足（3.15b）。
示例3.9 在示例3.6中，我们简要讨论了步骤hlm的计算，并认为我们也可以通过法线方程（3.13）对其进行计算。 如果μ不是很小，则矩阵条件良好，并且舍入误差不会有太大影响。
狗腿法的目的是在非线性方程组上也表现出色，即（3.17）是线性方程组的平方系统
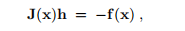
溶液h = hnr，则采用牛顿-拉夫森步骤，请参见示例3.2。 Ja cobian J可能是病态的（甚至是奇异的），在这种情况下，舍入误差往往是解决方案的主导。 如果我们使用（3.18a）来计算hgn，则会使此问题恶化。
在immoptibox的实现方法中，针对这些问题计算了（3.17）的解决方案。 如果J（x）的列不是线性独立的，则最小二乘解h不是唯一的，并且hgn被计算为具有最小范数的h。 此计算的一些详细信息在附录B中给出。
示例3.10 图3.5说明了从示例3.2和3.8中以起点x0 = [3，1]>，∆0 = 1且由ε1=ε2= 10-15，ε3给出的停止准则，适用于鲍威尔问题的Dog Leg方法的性能 = 10-20，kmax = 100。
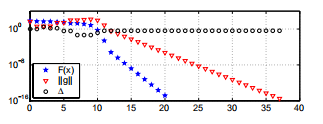
图3.5 狗腿法适用于鲍威尔的问题。
由于梯度小，迭代在37个步骤后停止，并返回x = [-2.41·10-35，1.26·10-9]>，这非常近似于x ∗ =0。如图3.3所示， 最终收敛是线性的（由奇异的J（x ∗）引起），但是比Marquardt方法要快得多。
示例3.11 对于示例1.1、3.4和3.7中的数据拟合问题，我们使用了算法3.21。 如例3.7所示，我们使用起点x0 = [−1，-2，1，-1]>，取∆0 = 1且由ε1=ε2=ε3= 10-8，kmax = 200给出的停止标准 该算法在经过30个迭代步骤后以x'[−4，-5，4，-4]>停止。 性能说明如下。 如图3.3所示，我们注意到非常快的最终收敛速度。
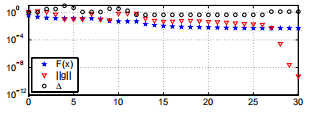
图3.6。 狗腿法适用于示例1.1中的拟合问题。
最后两个例子似乎表明，“狗腿法”比“ Levenberg-Marquardt法”要好得多。 当最小二乘问题来自非线性方程组时，这是正确的。 狗腿法目前被认为是求解非线性方程组的最佳方法。
对于一般的最小二乘问题，狗腿法与LM方法具有相同的劣势：如果F（x ∗）= 0，则最终收敛可以期望是线性的（且缓慢）。对于给定的问题和给定的开始猜测 x0不可能事先说出两种方法中哪一种更快。
3.4. 混合方法：LM和拟牛顿A Hybrid Method: L–M and Quasi–Newton
1988年，Madsen提出了一种混合方法，将L–M方法（如果F（x ∗）= 0则为二次收敛，否则为线性收敛）与Quasi5）-Newton方法相结合，即使F（x ∗）也具有超线性收敛。 =0。迭代从LM方法的一系列步骤开始。 如果性能表明F（x ∗）明显非零，则我们改用准牛顿法以获得更好的性能。 我们可能会发现有迹象表明，最好改回到LM方法，因此也有一种机制。
5)源自拉丁语：“准” =“几乎”。 有关准牛顿法的一般介绍，请参见Frandsen等人（2004年）的第5章。
如果条件满足，则切换到拟牛顿法
在三个连续成功的迭代步骤中得到满足。 这被解释为表明我们正在接近F *（x *）= 0且F（x *）明显非零的x *。 如结合（3.12）所述，这可能导致缓慢的线性收敛。
拟牛顿法基于在当前迭代x处具有近似于Hessian F''（x）的B，并且通过求解可以找到步骤hqn
这是牛顿方程（2.9a）的近似值。
近似值B通过BFGS策略进行更新，请参见Frandsen等人（2004年）的5.10节：近似值矩阵序列中的每个B都是对称的（与任何F''（x）一样）并且是正定的。 这样可确保hqn为“下坡”，参见（2.10）。 我们从对称的正定矩阵B0 = I开始，BFGS更新由要添加到当前B的2级矩阵组成。Madsen（1988）使用以下版本，由Al-Baali和Fletcher（1985）提出 ，
其中J = J（x），Jnew = J（xnew）。 如前所述，电流B是正定的，并且仅在h> y> 0时才改变。在这种情况下，可以证明新的B也是正定的。
拟牛顿法在迭代的全局阶段并不稳健。 它不能保证下降。 在解x ∗处，我们有F'（x ∗）= 0，并且迅速减小的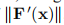
值指示出良好的最终收敛性。 如果这些标准值的下降速度不够快，那么我们将切换回L–M方法。
该算法总结如下。 它调用辅助函数LMstep和QNstep，实现这两种方法。
我们有以下几点评论：
1◦初始化。 可以通过（3.14）找到µ0。 停止标准由（3.15）给出。
2◦点表示我们还传输了f和J等的当前值，因此我们不必为相同的x重新计算它们。
3◦请注意，L-M和拟牛顿步骤都为Hessian矩阵的近似提供了信息。
下面给出了两个辅助功能：
我们对LMstep和QNstep函数有以下说明：
4◦像算法3.16一样，增益比％也用于更新µ。
5◦指示可能是时候切换方法了。 在算法3.25开始时，参数计数被初始化为零。
7◦我们将拟牛顿法与信任区域法结合在一起，并对边界有效的情况进行了简单处理，请参见第15f页。 在从L–M方法切换时，将∆初始化为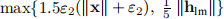
8◦未显示：∆通过（2.19）更新。
9◦在算法的这一部分中，我们着重于使F0接近零，因此我们接受F值的轻微增加，例如δ=√εM，其中εM是计算机的单位舍入。
10◦梯度下降得不够快。
示例3.12 注意，在更新公式（3.24）中，y的计算涉及乘积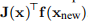
。 这意味着我们必须存储先前的雅可比矩阵。 相反，我们可以使用
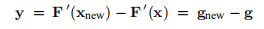
在更新公式中，但Madsen（1988）发现（3.24）表现更好。 Madsen（1988）中没有包括Q-N步骤中的信任区域方法，但是在immoptibox函数nlshybrid的开发过程中，发现这种想法可以提高性能。 它减少了徒劳尝试Q-N步骤的次数，即10°的条件立即返回到L-M方法。
示例3.13 对于示例3.7和3.8中讨论的问题，此混合方法的性能不会优于算法3.16。 在后一种情况下（参见图3.3），F（x）→0，并且永远不会满足注释5◦处的切换条件。 在前一种情况下，F（x ∗）明显为非零，但是-如示例3.7中所述-简单的LM方法具有所需的超线性最终收敛。
为了证明算法3.25的效率，我们考虑改进的Rosen brock问题，请参见Frandsen等人（1999年）的示例5.5，由f给出：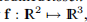
其中可以选择参数λ。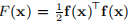
的极小值是
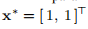，其中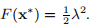
下面，我们给出一些值λ的算法3.16和3.25的结果。 在所有情况下，我们使用x0 = [-1.2，1]>，初始阻尼参数µ0由（3.14）中的τ= 10-3定义，并且（ε1，ε2，kmax）=（10-10，10-14， 200）中的停止条件（3.15）。
在前两种情况下，λ太小而不能真正影响迭代，但是对于较大的λ值，我们看到混合方法比简单的Levenberg-Marquardt算法要好得多-特别是在获得的精度方面。
在图3.7中，我们说明了两种算法在λ= 104的情况下的性能。
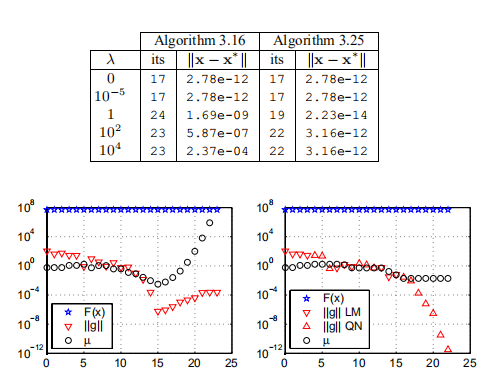
图3.7. Levenberg–Marquardt方法（左）和混合方法（右）
使用L–M方法后，所有步骤均不执行。 15未能改善目标功能； µ迅速增加，并且在步骤no满足停止标准（3.15b）。 23.对于混合方法，从步骤Nos开始，尝试了几种使用拟牛顿法的方法。 5、11和17。最后一次尝试成功，并且在22个步骤之后，迭代（3.15a）停止。
3.5. L–M方法的割线版本A Secant Version of the L–M Method
本手册中讨论的方法假定向量函数f是可微的，即雅可比行列式
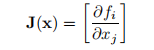
存在。 在许多实际的优化问题中，碰巧我们无法给出J中元素的公式，例如，因为f是由“黑匣子”给出的。 LM方法的割线版本适用于此类问题。
最简单的解决方法是将J（x）替换为通过数值微分获得的矩阵B：第（i，j）个元素通过有限差分近似法近似
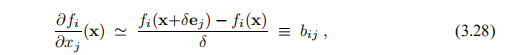
其中ej是第j坐标方向上的单位矢量，而δ是适当小的实数。 使用这种策略，每个迭代x都需要对f进行n + 1次评估，并且由于δ可能比距离kx-x ∗ k小得多，因此我们获得的关于f的全局行为的信息不会比仅评估时要多 f（x）。 我们想要更好的效率。
示例3.14 令m = n = 1并考虑一个非线性方程
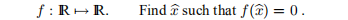
对于这个问题，我们可以将牛顿-拉夫森算法（3.6）编写为
如果我们无法实现f'（x），则可以将其近似为
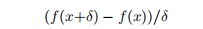
δ选择得适当小。 一般而言，我们可以用（3.29）替换为
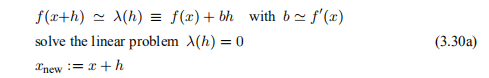
假设我们已经知道xprev和f（xprev）。 然后我们可以通过要求固定系数b（近似于f'（x））
这给出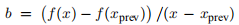
，通过选择b，我们将（3.30）视为割线方法，例如参见Elden等人（2004）的第70f页。
割线法相对于牛顿-拉夫森法的另一种有限差分近似法的主要优点是，每个迭代步骤只需要一个函数求值，而不是两个。
现在，考虑f的线性模型（3.7a）：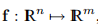
我们将替换为
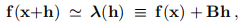
其中B是J（x）的当前近似值。 在下一个迭代步骤中，我们需要Bnew，以便
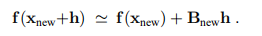
特别地，我们希望该模型对h = x-xnew相等，即
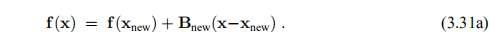
这给了我们Bnew的m·n个未知元素中的m个方程，因此我们需要更多条件。 Broyden（1965）建议用（3.31a）补充
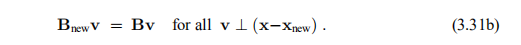
很容易验证是否满足条件（3.31a–b）
注意，在n = 1的情况下，条件（3.31a）对应于割线条件（3.30b）。我们说这种方法是广义割线方法。 具有此修改的算法3.16的中心部分的简要草图具有以下形式
鲍威尔表明，如果向量x0，x1，x2，...的集合收敛到x ∗，并且步骤{hk≡xk-xk-1}的集合满足{hk-n + 1，.....的条件。 对于每个k≥n，……，hk}是线性独立的（它们跨越整个IRn），则不管B0的选择如何，近似集{Bk}都收敛到J（x ∗）。
然而，实际上，经常会发生前n个步骤未覆盖整个IRn的情况，并且存在以下风险：在某些迭代步骤之后，当前B与真实的Jacobian矩阵的近似值如此之差，即-B> f （x）甚至不是下坡方向。 在这种情况下，x将保持不变，而µ会增加。 近似值B发生了变化，但是仍然可能是一个较差的近似值，从而导致µ的进一步增加等。最终，尽管x可能与x∗相距甚远，但由于hslm太小而无法满足（3.15b），因此该过程停止了。
已经提出了许多策略来克服这个问题，例如通过有限的差异偶尔对B进行重新计算。 在下面的Algo rithm 3.34中，我们用循环的，按坐标方式进行的一系列更新来补充由迭代过程确定的更新：令h表示当前步骤，令j表示当前坐标号。 如果h和ej之间的角度θ为“大”，则我们将计算J的第j列的有限差分近似值。更具体地说，如果
实验表明，（相当悲观的）选择γ= 0.8提供了良好的性能。 通过这种选择，我们可以预期每个迭代步骤（几乎）需要向量函数f的两次评估。
现在我们准备介绍该算法。 阻尼参数µ的监控与算法3.16相同，为清楚起见，我们在演示中将其省略。
我们有以下几点评论：
1◦初始化。 输入x0，输入B0或由（3.28）计算。 停止标准（3.15）中的参数和（3.28）中使用的步距δ也是输入值。
2◦Cf（3.33）。 mod（j，n）是除以n后的余数。
3◦步骤η由xj = 0给出，
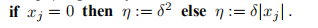
4◦仅在满足下降条件（2.1）的情况下更新迭代x，而近似值B在每一步中都更新。 因此，当f（x）不变时，近似梯度g也可能改变。
示例3.15 我们对例3.13中的修正Rosenbrock问题使用了算法3.34，其中λ=0。如果我们使用与该例相同的起点和终点准则，并且差近似（3.28）中的δ= 10−7，我们发现 29个迭代步骤后的解，涉及f（x）的53个评估。 为了进行比较，“真正的” LM算法仅需17个步骤，这意味着总共对f（x）和J（x）进行了18次评估。
我们还对测试1.1、3.7和3.11中的数据拟合问题使用了割线算法。 在δ= 10-7且起点和停止条件与示例3.7相同的情况下，迭代在94个步骤后被（3.15a）停止，涉及f（x）的总共192次评估。 为了进行比较，算法3.16需要62个迭代步骤。
这两个问题表明算法3.34是健壮的，但它们也说明了一条一般的经验法则：如果有梯度信息可用，通常使用它是值得的。
在许多应用中，数字m和n很大，但是每个函数fi（x）仅取决于x中的一些元素。 在那种情况下，大多数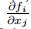
为零，我们说J（x）是一个稀疏矩阵。 在Levenberg-Marquardt方程（3.13）的解中，有一些利用稀疏性的有效方法，例如，Nielsen（1997）。 但是，在更新公式（3.32）中，向量h和u中的所有元素通常都不为零，因此Bnew将是一个密集矩阵。 讨论如何解决这个问题超出了本手册的范围。 我们指的是Gill等人（1984）和Toint（1987）。
3.6. 狗腿法的割线版本 A Secant Version of the Dog Leg Method
使用割线近似于雅可比行列的想法当然也可以与3.3节中的“狗腿法”结合使用。 在本节中，我们将考虑m = n的特殊情况，即在非线性方程组的解中。 Broyden（1965）不仅给出了定义3.32中的公式，
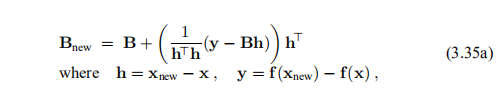
用于更新近似雅可比行列式。 他还给出了一个公式，用于更新雅可比行列的近似逆D'J（x）-1。 公式是
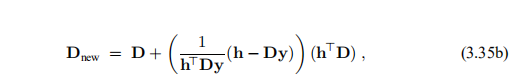
其中h和y在（3.35a）中定义。
对于这些矩阵，最陡的下降方向hsd和高斯–牛顿步长（在这种情况下与牛顿步长相同，参见示例3.5），hgn（3.18）近似为
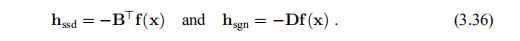
可以轻松修改算法3.21以使用这些近似值。 初始B = B0可以通过差分近似（3.28）求出，D0计算为B-1 0。 很容易表明，那么当前的B和D满足BD =I。步长参数α由（3.19）找到，而J（x）由B代替。
像L–M方法的割线版本一样，此方法需要额外的更新，以使B和D保持与当前Jacobian及其逆的良好近似。 我们发现围绕（3.33）讨论的策略在这种情况下也很好用。 还应该提到的是，（3.35b）中的分母可以为零或非常小。 如果
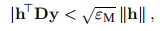
那么D不更新，而是按D = B-1计算。
用（3.35）进行的每次更新都会“耗费” 10n2触发器6），通过（3.36）计算两个阶跃向量，再通过（3.19）来计算α，则需要6n2触发器。 因此，使用Dog Leg方法的无梯度版本的每个迭代步骤的成本约为16n2触发器加上f（xnew）的评估。 对于比较而言，采用算法3.21的每一步的成本约为23n3 + 6n2触发器，加上f（xnew）和J（xnew）的评估。 因此，对于较大的n值，无梯度版本每步便宜。 但是，迭代步骤的数量通常要大得多，如果可以使用雅可比矩阵，则梯度版本通常会更快。
6）一个“翻牌”是两个浮点数之间的简单算术运算。
示例3.16 我们在Rosenbrock函数f：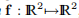
上使用了算法3.21和无梯度Dog Leg方法，由
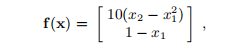
参见示例3.13。 该函数具有一个根，x ∗ = [1，1]>，在两种方法中，我们都使用起始点x0 = [-1.2，1]>和ε1=ε2= 10-12，kmax = 100作为停止准则 （3.15），而（3.28）中的δ= 10-7。 Algo rithm 3.21在17个迭代步骤后，即在对f及其雅可比行列式进行18次评估后，在求解处停止。 割线版本也停止了解决方案。 这需要28个迭代步骤和总共49次f评估。
3.7。 结束语Final Remarks
我们讨论了许多用于解决非线性最小二乘问题的算法。 它们全部出现在任何好的程序库中，并且可以通过Internet地址上的GAMS（可用数学软件指南）找到实现。
本手册中的示例是在MATLAB中计算的。 程序可在工具箱immoptibox中获得，该工具箱可从以下网址获得：
，问题的形式为：找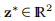
使得f（z ∗）= 0，其中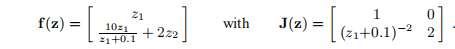
对于所有z，该雅可比行列都是非奇异的。 在停止准则中起点为z0 = [3，1]>，τ= 10-16和ε1=ε2= 10-15的LM算法3.16
（3.15）使用z'[-1.40e-25，9.77e-25]> 3个步骤后停止。 这是z ∗ = 0的良好近似值。
其中，对于给定的x，找到向量c = c（x）∈IR2作为线性问题的最小二乘解
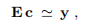
其中
。 与示例1.1中一样，函数f由
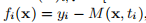由（E）i行给出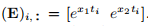
定义，导致
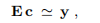
其中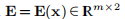
由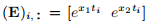
行给出。 与示例1.1中一样，函数f由f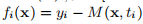
定义，导致
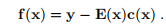
可以证明雅可比矩阵是
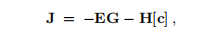
其中，对于任何向量u，我们定义对角矩阵[u] = diag（u），并且
算法3.16具有与示例3.7相同的较差的开始猜测，x0 = [-1，-2]>，τ= 10-3且ε1=ε2= 10-8得出解x'[-4，-5]> 经过13个迭代步骤； 大约是4参数模型所需步数的15。这种方法可以推广到其中某些参数线性出现的任何模型。 它具有可分离的最小二乘法的名称，例如在Nielsen（2000）和Golub and Pereyra（2003）中进行了讨论。
最小时，算法最有效。 具有相同的数量级。
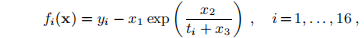
替代公式是
然后，对于第一个公式，在175个迭代步骤之后，迭代将由（3.15b）停止，而在按比例缩放的情况下，在88个步骤之后，迭代将由（3.15a）停止。
A.对称的正定矩阵
如果A = AT，即aij = aji对于所有i，j，矩阵A∈IRn×n是对称的
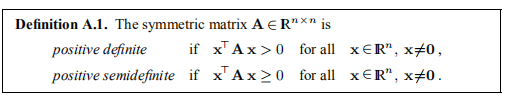
此类定理的一些有用属性在下面的定理A.2中列出。 可以通过将几乎所有关于线性代数和数值线性代数的教科书中的定理结合起来找到证明。 在本附录的最后，我们给出了该定理的一些实际含义。
显示A为正半定数。 如果m≥n并且J中的列线性独立，则x ≠ 0⇒y ≠ 0且y> y>0。因此，在这种情况下，A为正定。
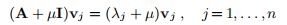
对于任何μ∈IR。 将其与定理A.2中的2◦相结合，我们可以看到，如果A是对称的且为半正定的且µ> 0，则矩阵A + µI也是对称的，并且可以保证为正定的。
定理A.2。 令A∈IRn×n是对称的，令A = LU，其中L是单位下三角矩阵，U是上三角矩阵。 此外，令{（λj，vj）} nj = 1表示A的本征解，即
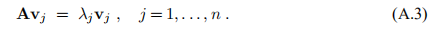
然后
1◦特征值是实数，λj∈IR，特征向量{vj}构成IRn的正交基。 2◦以下语句等效：a）A是正定（正半定）
b）所有λj> 0（λj≥0）
c）所有uii> 0（uii≥0）。
如果A为正定，则
3◦LU分解在数值上是稳定的。
4◦U = DL>，D = diag（uii）。 5◦A = C> C，即Cholesky分解。 C∈IRn×n是上三角。
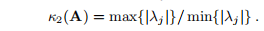
如果A为正（半）定且µ> 0，则
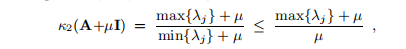
这是µ的递减函数。
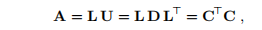
显示
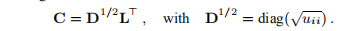
可以通过以下算法直接计算Cholesky因式分解（即，没有中间结果L和U），该算法包括正定性检验。
该算法的“成本”约为
触发器。 一旦计算出C，就可以通过正向和反向替换来求解系统Ax = b
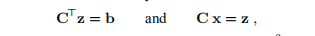
分别。 每个步骤的费用约为n2触发器
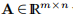且m≥n且b∈IRm，求h∈IRn使得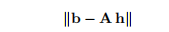
被最小化。 为了对此进行分析，我们将使用A的奇异值分解（SVD），
矩阵U∈IRm×m和V∈IRn×n正交
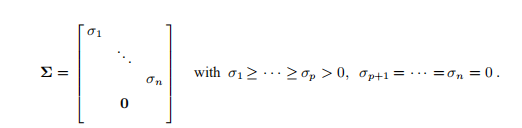
σj是奇异值。 p是A的秩，等于子空间R（A）⊆IRm的尺寸（所谓的A范围），该子空间包含A列的每种可能的线性组合。
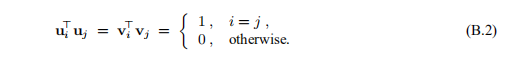
从（B.1）和（B.2）中可以得出
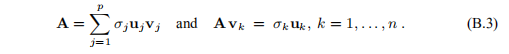
{uj}和{vj}可以分别用作IRm和IRn中的正交基，因此我们可以编写
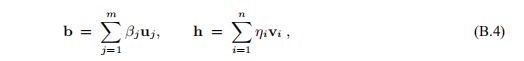
通过使用（B.3），我们看到
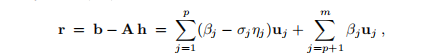
并借助（B.2）
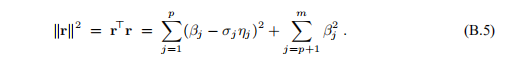
最小化
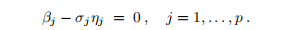
因此，最小二乘解可以表示为
当p <n时，最小二乘解具有n-p个自由度：ηp+ 1，...，ηn是任意的。 与关于（B.5）的讨论类似，我们看到当ηp+ 1 =··=ηn= 0时kh ∗ k最小。对应于自由参数选择的解决方案是所谓的最小范数解，
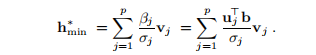
重新制定源自（B.4）和（B.2）。
