数据结构(二) - 线性表

目录

定义

线性表是具有相同特性的数据元素的一个有限序列

  • 线性表中数据元素的类型可以为简单类型，也可以为复杂类型
  • 许多实际应用问题所设计的基本操作有很大的相似性，不应为每个具体应用单独编写一个程序
  • 从具体应用中抽象出共性的逻辑结构和基本操作(抽象数据类型)，然后实现其存储结构和基本操作

抽象数据类型线性表的定以：

线性表的顺序存储表示

线性表的顺序表示又称为顺序存储结构或存储映像

顺序存储定义: 把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构

  • 线形表顺序存储结构占用一片连续的存储空间。知道某个元素的存储位置就可以计算其他元素的存储位置

顺序表的查找算法分析

  • 平均查找长度ASL(Average Search Length):
    为确定记录在表中的位置，需要与给定值进行比较的关键字的个数的期望值叫做查找算法的平均查找长度

时间复杂度：T(n) = O((n+1)/2) = O(n)

顺序表的插入算法分析

规律：移动次数和插入位置的和是n+1

i + x = n + 1

x: 移动次数
i： 插入位置
n：顺序表元素的个数

补充下：

其中i表示下界，n表示上界， k从i开始取数，一直取到n,全部加起来；

顺序表总结

  • 时间复杂度：查找、插入、删除算法的平均时间复杂度为O(n)
  • 空间复杂度：显然，顺序表操作算法的空间复杂度S(n)=O(1), 没有占用辅助空间

优点：

  • 存储密度大(节点本身所占存储量/结点结构所占存储量=1)
  • 可以随机存取表中任一元素

缺点：

  • 在插入、删除某一元素时，需要移动大量元素
  • 浪费存储空间
  • 属于静态存储形式，数据元素的个数不能自由扩充

线性表的链式表示

链表存储的特点：

单链表、双链表、循环链表

相关术语

  • 结点： 数据元素的存储映像。由数据域和指针域两部分组成
  • 链表： n个结点由指针链组成一个链表。它时线性表的链式存储映像，称为线性表的链式存储结构

  • 头指针：是指向链表中第一个结点的指针
  • 头结点： 是在链表的首元结点之前附设的一个结点
  • 首元结点：是指链表中存储第一个数据元素a1的结点

空表：

有头结点的空表:

头结点的数数据域装的是什么？

头结点的数据域可以为空，也可以存放线性表长度等附加信息，但此节点不能计入链表长度值

链表算法

  • 单链表的销毁
    从头指针开始，依次释放所有结点

  • 单链表的清空
    链表仍存在，但链表中无元素，成为空链表(头指针和头结点仍然再)

  • 求链表的长度

  • 取第i个元素

  • 按值查找

  • 在第i个元素前插入元素e
    思路：1.怎么找到第i-1个元素。 2.怎么将e插入进链表

  • 删除第i个元素

算法分析：

  • 查找
    因为线性表只能顺序存取，即在查找时要从头指针找起，查找的时间复杂度为O(n)

  • 插入和删除

    • 因线性表不需要移动元素，只要修改指针，一般情况下时间复杂度为O(1)
    • 如果不知道插入和删除的位置，由于要从头查找前驱结点，所耗时间复杂度为O(n)

单链表的创建

头插法: 元素插入到链表头部， 也叫做前插法

算法描述：

尾插法：元素插入在链表的尾部，也叫后插法

算法描述：

循环链表

 是一种头尾相接的链表(即: 表中最后一个结点的指针域指向头结点，整个链表形成一个环)

优点：从表中任一结点出发均可找到表中其他结点

从尾结点找头结点，比较容易，但是从头节点找尾结点就比较麻烦

算法：两个双向链表的合并

双向链表

在单链表的每个结点里再增加一个指向其直接前驱的指针域 prior，这样链表中就形成了有两个方向不同的链，故称为双向链表

双向循环列表：

插入和删除的时间复杂度为：O(n)

双向链表的插入

插入s 结点：

双向链表的删除

删除p结点：

单链表、循环链表、双向链表的时间效率比较

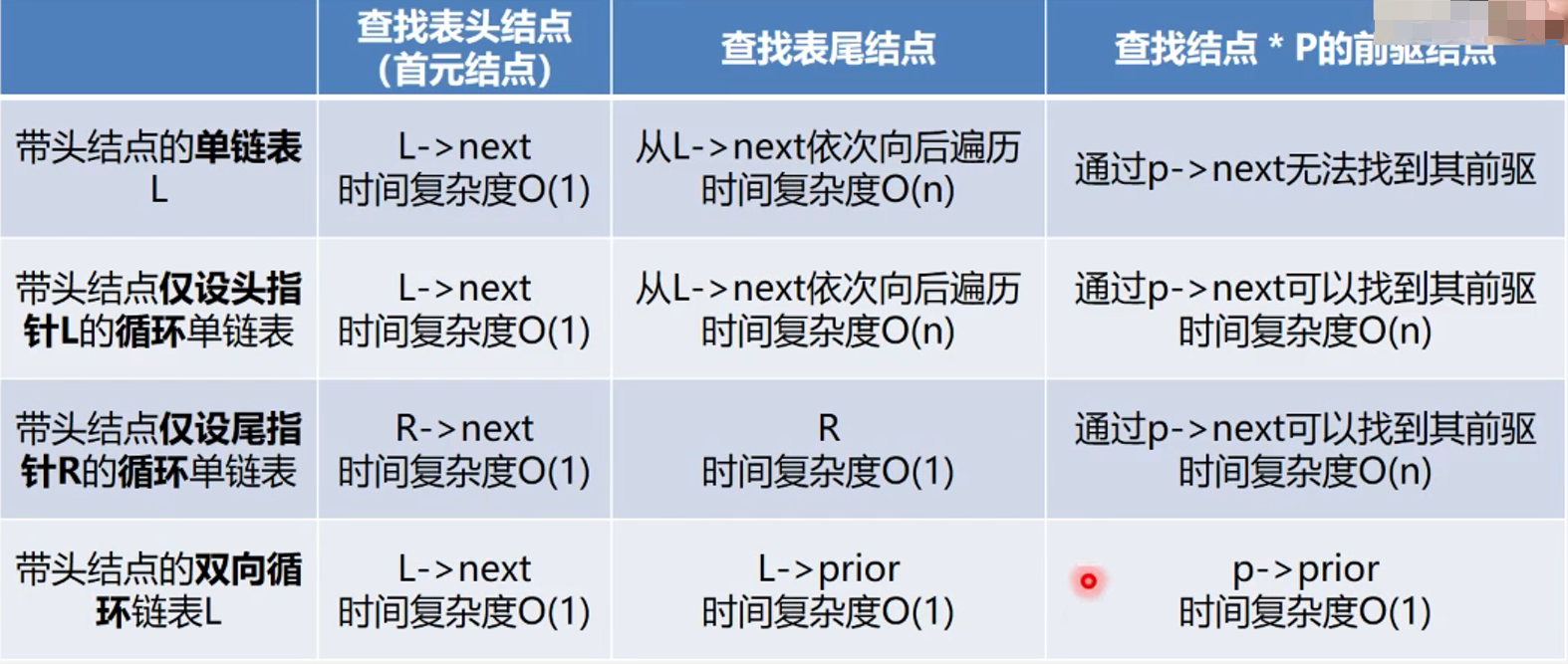
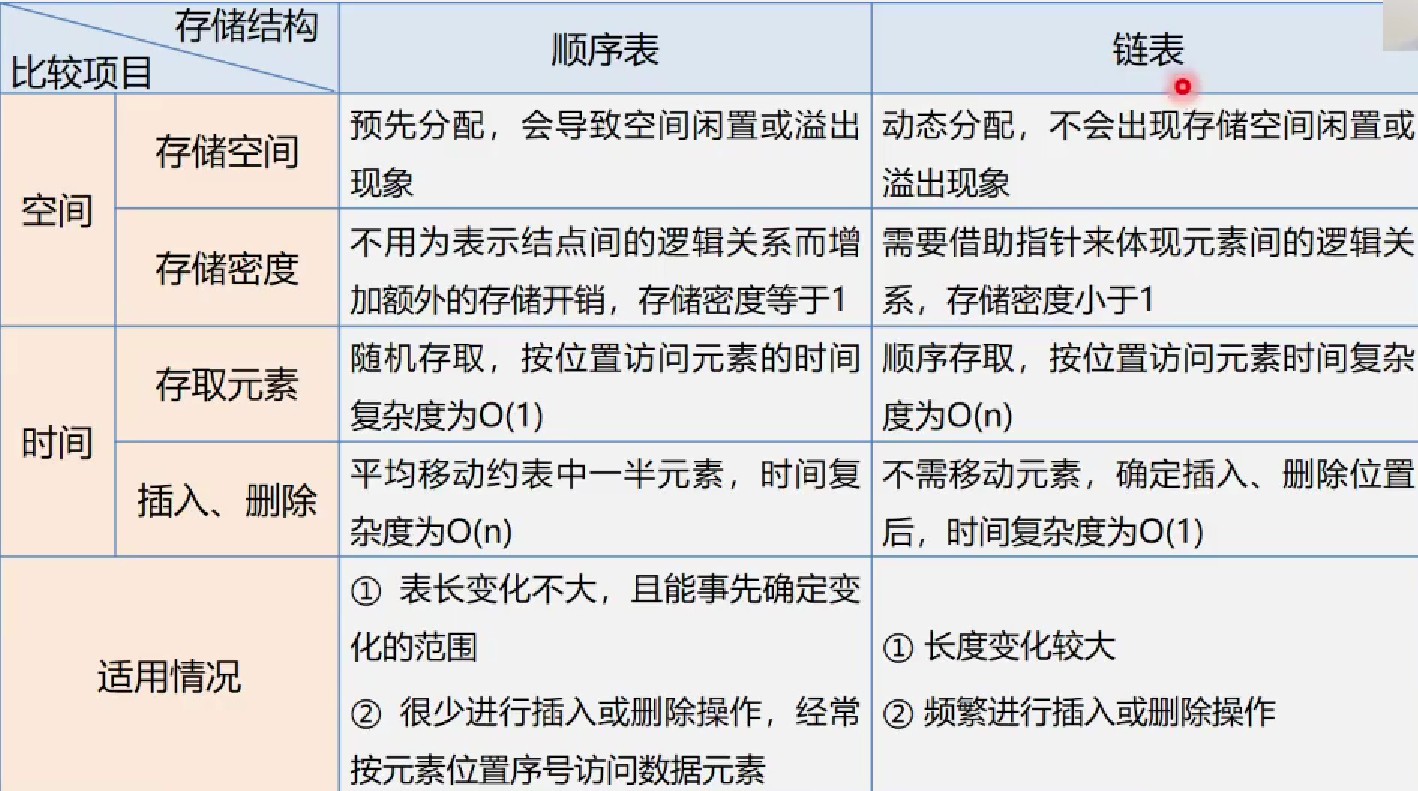
顺序表和链表的比较

  • 链式存储结构的优点

    • 结点空间可以动态申请和释放
    • 数据元素的逻辑次序靠结点的指针来指示，插入和删除时不需要移动数据元素

  • 链式存储结构的缺点

    • 存储密度小，每个结点的指针域需额外占用存储空间。当每个结点的数据域所占字节不多时，指针域所占存储空间的比重显得很大。
    • 链式存储结构时非随机存储结构。对任一结点的操作都要从头指针查找到该结点，这增加了算法的复杂度

tips：

存储密度：指结点数据本身所占的存储量和整个结点结构中所占的存储量之比

即：存储密度 = 结点数据本身占用的空间/结点所占的空间总量

一般地，存储密度越大，存储空间的利用率就越高。显然，顺序表的存储密度为1(100%)，而链表的存储密度小于1.

posted @ 2022-03-20 16:02  chuangzhou  阅读(309)  评论(0)  编辑  收藏  举报