浅谈字典树Trie
\(\;\)
本文是作者学习《算法竞赛进阶指南》的所得,有些语言是摘自其中。
\(\;\)
基础知识
定义
\(\;\)
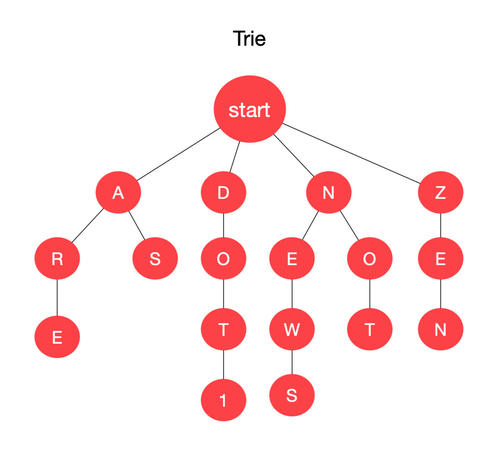
字典树(Trie):是一种支持字符串查询的多叉树结构。其中的每个节点,都有字符指针,指向了它的若干个儿子。
如图:
\(\;\)
空间复杂度
\(\;\)
\(O(NC)\)
其中\(N\)是节点个数,\(C\)是字符集的大小。
\(\;\)
Insert
\(\;\)
找到这个字符串在Trie中的最大前缀,把前缀后面的部分插到这个节点的后面
code
void Insert(char* str,int root)
{
int len = strlen(str);
for(int i=0;i<len;i++)
{
int c = str[i] - 'a'; //转成数字存储
if(!trie[root][c]) trie[root][c] = ++idx; //若指针为空,就新建一个指向c的指针
root = trie[root][c]; //然后继续往下遍历
}
}
Query
\(\;\)
不断地通过字符指针向下检索。直到字符指针为空,或者查询完毕为止。
code
bool Query(char* str,int root)
{
int len = strlen(str);
for(int i=0;i<len;i++)
{
int c = str[i] - 'a';
root = trie[root][c];
if(root == 0) return false; //若指针为空,则字符串不存在
}
return true;
}
Problem 1
\(\;\)
题意
\(\;\)
有\(n\)个字符串\(S_1,S_2,\cdots,S_n\)。接下来有\(M\)次询问,每次询问给定一个字符串\(T\),求\(S_1-S_n\)有多少个字符串是\(T\)的前缀。
其中输入字符串的总长度不超过\(10^6\)
\(\;\)
做法
\(\;\)
我们把\(S_1,S_2,\cdots,S_n\)这些字符串插到一棵字典树里。(参考Insert操作)。在插入的同时,顺便在每个节点上记录一个\(cnt\),表示多少个字符串在这里结尾。
然后对于每次询问,我们在字典树中查询这个字符串\(T\)。在查询过程中,累加上节点上\(cnt\)所得结果就是答案。
其实相当于对\(T\)的每个前缀算一下贡献。
\(\;\)
code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000010;
char str[N];
int n, m, tree[N][26], root, idx, end_cnt[N];
void Insert(char* str,int root)
{
int len = strlen(str);
for(int i=0;i<len;i++)
{
int c = str[i] - 'a';
if(!tree[root][c]) tree[root][c] = ++idx;
root = tree[root][c];
}
end_cnt[root] ++;
}
int Query(char* str,int root)
{
int len = strlen(str), res = 0;
for(int i=0;i<len;i++)
{
int c = str[i] - 'a';
root = tree[root][c];
if(root == 0) break;
res += end_cnt[root];
}
return res;
}
int main()
{
cin >> n >> m;
while( n-- )
{
scanf("%s",str);
Insert(str,root);
}
while( m -- )
{
scanf("%s",str);
printf("%d\n",Query(str,root));
}
return 0;
}
\(\;\)
Problem 2
\(\;\)
题意
\(\;\)
给定一颗\(n\)个节点的树,树的每条边都有一个权值。从中选择两个点\(x,y\)。使得\(x\)到\(y\)的路径上的所有边权\(xor\)(异或)起来,得到的结果最大是多少?
\(n\leq 10^5\),边权\(\leq 2^{31}-1\)
\(\;\)
转化
\(\;\)
单看路径不太好搞,但是有一个比较套路的性质。
我们定义\(d(x)\)表示\(x\)到根节点\(root\)上边权的异或值
可以发现:对于两个点\(x\)到\(y\)路径上的异或值\(=d(x)\;xor\;d(y)\),因为它们\(LCA\)以上的点都被异或没了(\(a\;xor\;a=0\))。
因此我们要算的其实就是:在\(d(1),d(2),\cdots,d(n)\)中选出两个数,使得它们的异或值最大。
\(\;\)
01字典树
\(\;\)
我们可以把每个数拆分成二进制,因此,我们可以把数看作一个长度为\(31\)的\(01\)串(数值较小时在前补前导\(0\)),插到字典树中(其中最低二进制位为叶子节点)。
接下来,我们对于\(d(i)\)在\(Trie\)中进行一次与\(Query\)类似的操作。由于\(xor\)运算相同得\(0\),不同得\(1\)的性质,每次我们都贪心往与当前位相反的指针向下访问。若与当前位相反的指针为空,则只好访问与\(d(i)\)当前位相同的指针。根据这样的贪心策略,我们可以找到最优解。
\(\;\)
code
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 3000010;
#define PII pair<int,int>
int n, son[M][2], root, idx, d[N], res;
vector<PII> G[N];
void Dfs(int u,int fa)
{
for(int i=0;i<G[u].size();i++)
{
int v = G[u][i].first;
if(v == fa) continue;
d[v] = G[u][i].second ^ d[u];
Dfs(v,u);
}
}
void Insert(int root,int x)
{
for(int i=30;~i;i--)
{
int s = x >> i & 1;
if(!son[root][s]) son[root][s] = ++idx;
root = son[root][s];
}
}
int Query(int root,int x)
{
int res = 0;
for(int i=30;~i;i--)
{
int s = x >> i & 1;
if(son[root][s ^ 1])
{
res += 1 << i;
root = son[root][s ^ 1];
}
else
{
root = son[root][s];
}
}
return res;
}
int main()
{
cin >> n;
for(int i=1;i<n;i++)
{
int u, v, w;
scanf("%d%d%d",&u,&v,&w);
G[u].push_back( make_pair (v, w) );
G[v].push_back( make_pair (u, w) );
}
Dfs(1,0);
for(int i=1;i<=n;i++)Insert(root, d[i]);
for(int i=1;i<=n;i++)res = max(res, Query(root, d[i]));
printf("%d",res);
return 0;
}
可持久化Trie
\(\;\)
相比于只能维护最新状态的普通的数据结构,可持久化的数据结构可以知道任意时间的历史状态。
它具体是如何实现的?
朴素想法:在每次修改后把整个数据结构\(copy\)一遍。但这样的时间、空间复杂度都是\(O(nm)\)的。(\(n\)为数据结构大小,\(m\)为版本个数)
而可持久化提供了我们一种思想:每次只记录发生变化的部分,这样时间复杂度并无增加,而空间复杂度只会增加与时间同级的规模。
例如:线段树,每次修改至多变化\(log(n)\)个节点,则空间就只会增加\(log(n)\)
下面给大家模拟一下可持久化Trie的过程。
\(\;\)
模拟过程
\(\;\)
1.设当前根节点为\(root\),令\(p=root,idx=0\)
2.建立一个新的节点\(q\),令\(root'=q\)
3.若\(p\)不为空,则对于每种字符\(c\),令\(trie[q][c]=trie[p][c]\)
4.建立一个新的节点:\(trie[q][str_i]=++idx\)。
(而3,4操作其实就是除了字符\(str_i\)外,其他的信息完全相同)
5.令\(p=trie[p][str_i],q=trie[q][str_i]\)(向下遍历)
然后重复\(3-5\)的步骤,直到\(q\)到字符串末尾
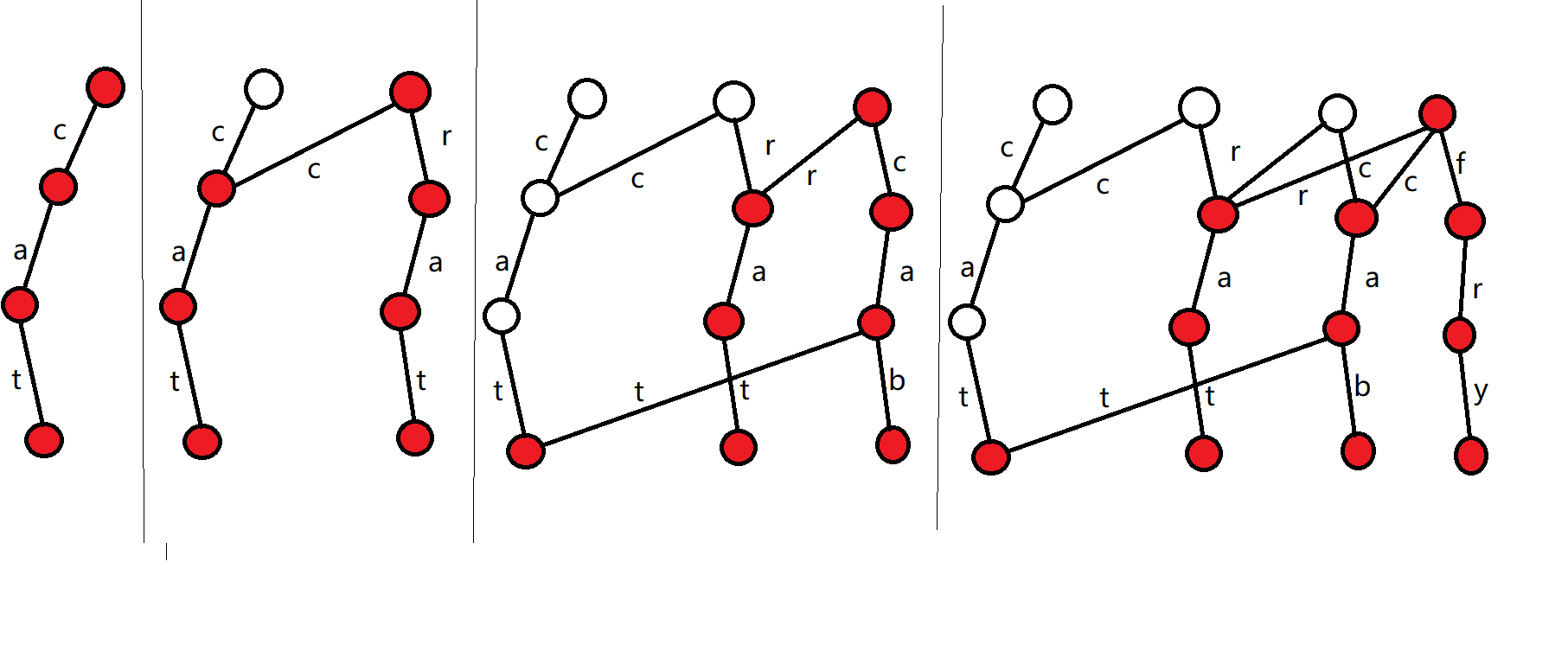
图中展示了在可持久化Trie中依次插入\(cat,rat,cab,fry\)的过程。
通过这样的操作,我们就可以得到4个版本的Trie了。
\(\;\)
\(\;\)
Problem 1
\(\;\)
给定一个非负整数序列 \(a\),初始长度为\(n\)。
有 \(m\) 个操作,有以下两种操作类型:
\(A\;\;x\):添加操作,表示在序列末尾添加一个数 \(x\),序列的长度加一。
\(Q\;\;l\;\;r\;\;x\):询问操作,你需要找到一个位置 \(p\),满足\(l\leq p\leq r\),使得:\(a[p] \;xor \;a[p+1]\;xor\; \cdots \;xor\; a[n] \;xor\;x\) 尽可能的大,输出最大值是多少。
\(n,m\leq 3\times 10^5,a[i]\leq 10^7\)
\(\;\)
前缀和
\(\;\)
一般这种一段区间的异或和我们都用前缀和的思路来做。
令\(s_i=a[1]\;xor \;\cdots \;xor\;a[i]\),显然\(a[l] \;xor \;a[l+1]\;xor\; \cdots \;xor\; a[r]=s_{l-1}\;xor\;s_r\)
令\(k=s_n\;xor\;x\)
也就是说:我们要找到一个\(p\;(l-1\leq p\leq r-1),\)使得\(s_p\;xor\;k\)最大。
如果不考虑\(l-1,r-1\)的限制,那么这道题就是我们前面讲的那个\(Problem\;2\)。
但是现在有限制,如何操作?
\(\;\)
可持久化
\(\;\)
这就要用到可持久化的精髓了。既然\(p\leq r-1\),则\(p\)一定是第\(r-1\)个版本中的\(s_i\)。
右端点处理完了,左端点?
由于我们不可以取\(<l-1\)的\(s_i\),则我们记录一个信息\(maxid[u]\),表示\(Trie\)中以\(u\)为根的子树中以某个二进制数为结尾的\(s_i\)的\(i\)最大是多少。
例如:以\(u\)为根的子树中,有以\(s_1,s_3,s_7\)为结尾的节点,则\(maxid[u]=7\)。
那么,在贪心找相反的指针时,如果这颗子树的\(maxid\)大于\(\geq l-1\),说明其中至少有一个数的编号是\(\geq l-1\)的,我们就可以往其中遍历,否则只能往相同的指针方向走了。
由于插入的时候要维护\(maxid\)这个信息,所以我们采用递归的方式来写。
时间复杂度:\(O((n+m)\;log\;10^7)\)
\(\;\)
code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 600010, M = N * 24;
int n, q, s[N], tree[M][2], root[N], idx, max_id[M];
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void Insert(int Bits, int Now, int Last, int t)
{
if(Bits < 0)
{
max_id[Now] = t;
return;
}
int v = s[t] >> Bits & 1;
if(Last) tree[Now][v ^ 1] = tree[Last][v ^ 1];
tree[Now][v] = ++idx;
Insert(Bits - 1,tree[Now][v],tree[Last][v],t);
max_id[Now] = max(max_id[tree[Now][0]],max_id[tree[Now][1]]);
}
int Query(int Now, int k, int L)
{
for(int i=23;i>=0;i--)
{
int v = k >> i & 1;
if(tree[Now][v ^ 1] && max_id[tree[Now][v ^ 1]] >= L)Now = tree[Now][v ^ 1];
else Now = tree[Now][v];
}
return k ^ s[max_id[Now]];
}
int main()
{
n = read(); q = read();
root[0] = ++idx;
Insert(23,root[0],0,0);
for(int i=1;i<=n;i++)
{
s[i] = read();
s[i] ^= s[i - 1];
root[i] = ++idx;
Insert(23, root[i], root[i-1], i);
}
while( q-- )
{
char op[2];
scanf("%s",op);
if(op[0] == 'A')
{
n ++;
s[n] = read();
s[n] ^= s[n - 1];
root[n] = ++idx;
Insert(23, root[n], root[n - 1], n);
}
else
{
int l, r, x;
l = read(); r = read(); x = read();
int t = s[n] ^ x;
printf("%d\n",Query(root[r - 1], t, l - 1));
}
}
return 0;
}


