旋转卡壳1——凸包
一、前驱知识：
1.叉积：A×B
A.x*B.y-A.y*B.x
>0 A在B的顺时针方向
<0 A在B的逆时针方向
2.点积：A·B
A.x*B.x+A.y+B.y
3.两点之间距离：
可以用点积方便的求解，即：
sqrt(A.x*A.x+A.y*A.y);
4.计算几何精度问题：
dcmp函数，直接看注解
5.计算几何问题，一般把他们打包在一起，形成以下代码：
代码：
struct Point{
double x,y;
Point(double xx=0,double yy=0):x(xx),y(yy){}
Point operator+(const Point &p){return Point(x+p.x,y+p.y);}
Point operator-(const Point &p){return Point(x-p.x,y-p.y);}
Point operator*(const int k){return Point(k*x,k*y);}
bool operator<(Point &p)const
{
if(x<p.x) return 1;
else if(x==p.x)
return y<=p.y;
else
return 0;
}
double dot(const Point &p){return x*p.x+y*p.y;}
double det(const Point &p){return x*p.y-y*p.x;}
};
const int maxn=5e4+10;
Point P[maxn],Res[maxn];
inline int DCMP(double x)
{
if(fabs(x)<EPS)
return 0; //注意：这里是返回0,如果差值非常小（不管是正非常小还是负非常小），都返回0，即假，即：不处理了，等待下次处理。也就是卡精度
else
return x<0?-1:1;
}
inline double cross(Point A,Point B,Point C)
{
return (B-A).det(C-A);
}
inline double multi(Point A,Point B,Point C)
{
return (B-A).dot(C-A);
}
inline double dist(Point A,Point B)
{
return (B-A).dot(B-A);
// return (A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);
}
二、引入凸包：
旋转卡壳问题，第一步首先是要建立凸包，凸包是什么呢？
凸包就是：
那么如何建立一个凸包？
这里我们讲的是Graham扫描法。
**
三、正题开始：
**
1.首先题目会给出一系列的点：
2.把他们按照如下顺序排序：
1找到最①下②左的点（基准点） swap成为P[0]
2与P[0]极角从小到大
3极角相等，则与P[0]距离从小到大的顺序
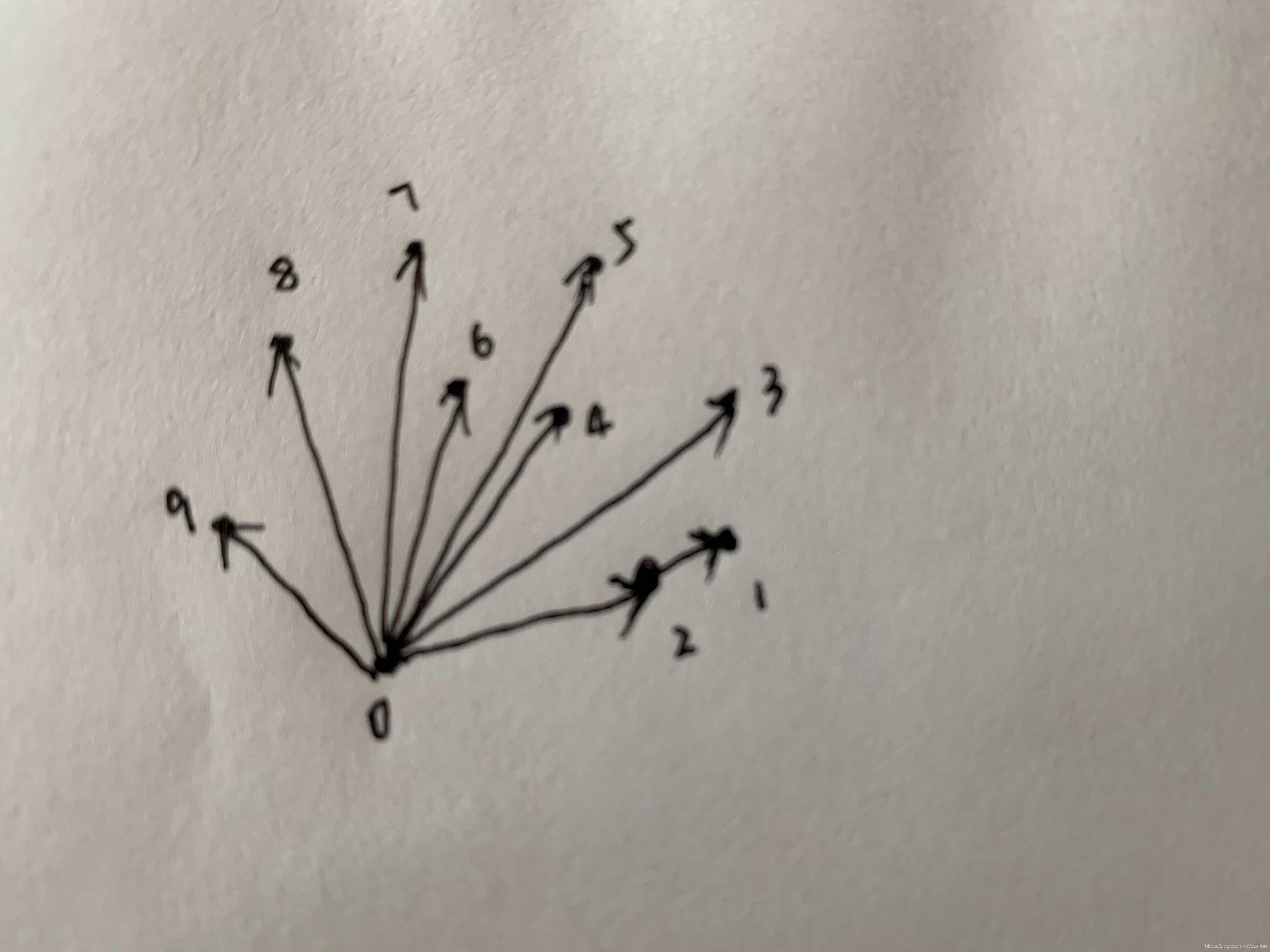如上图，0是基准点。1 2极角相等，则按距离排，其他的按极角排。
排序代码：
inline bool cmp(Point &A,Point &B)
{
if(cross(P[0],A,B)>0)
return 1;
if(cross(P[0],A,B)==0)
return dist(P[0],A)<dist(P[0],B);
return 0;
}
3.放缩凸壳：（为什么用放缩这个词，好好琢磨琢磨就明白了）
第一种情况对应上图的1，第三种情况对应上图的4,6，都会被放缩掉。只有第二种情况，凸壳会向下延展。
int top=0;
Res[top]=P[0]; //第一个点是我们找出来的最下左的点，一定在凸包里
for(int i=1;i<N;i++)
{
while(top>0 && cross(Res[top],Res[top-1],P[i])>=0)//记住cross顺序，看上面的图就会明白，在这个循环里说明在放缩，也就是在1 3两种情况里
top--;
Res[++top]=P[i];//延展
}
完整代码：
/*
凸包
by adl
2021-3-28
*/
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<stack>
#define ll long long
#define INF 0x3f3f3f3f
#define EPS 1E-10
using namespace std;
const int maxn=5e4+10;
struct Point{
double x,y;
Point(double xx=0,double yy=0):x(xx),y(yy){}
Point operator+(const Point &p){return Point(x+p.x,y+p.y);}
Point operator-(const Point &p){return Point(x-p.x,y-p.y);}
Point operator*(const int k){return Point(k*x,k*y);}
bool operator<(Point &p)const
{
if(x<p.x) return 1;
else if(x==p.x)
return y<=p.y;
else
return 0;
}
double dot(const Point &p){return x*p.x+y*p.y;}
double det(const Point &p){return x*p.y-y*p.x;}
};
Point P[maxn],Res[maxn];
inline int DCMP(double x)
{
if(fabs(x)<EPS)
return 0; //注意：这里是返回0,如果差值非常小，就返回0，即假，即：不处理了，等待下次处理。也就是卡精度
else
return x<0?-1:1;
}
inline double cross(Point A,Point B,Point C)
{
return (B-A).det(C-A);
}
double multi(Point A,Point B,Point C)
{
return (B-A).dot(C-A);
}
inline double dist(Point A,Point B)
{
return (B-A).dot(B-A);
// return (A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y);
}
void Print(Point* P,int N)
{
cout<<"+++++++++++++++++++++"<<endl;
for(int i=0;i<N;i++)
cout<<P[i].x<<" "<<P[i].y<<endl;
cout<<"+++++++++++++++++++++"<<endl;
}
inline bool cmp(Point &A,Point &B)
{
if(cross(P[0],A,B)>0)
return 1;
if(cross(P[0],A,B)==0)
return dist(P[0],A)<dist(P[0],B);
return 0;
}
int Graham(Point* P,Point*Res,int N)
{
int init=0;
for(int i=1;i<N;i++)
{
if(P[i].y<P[init].y)
init=i;
else if(P[i].y==P[init].y && P[i].x<P[init].x)
init=i;
}
swap(P[init],P[0]);
sort(P+1,P+N,cmp);
Print(P,N);
int top=0;
Res[top]=P[0];
for(int i=1;i<N;i++)
{
while(top>0 && cross(Res[top],Res[top-1],P[i])>=0)
top--;
Res[++top]=P[i];
}
return top+1;
}
int main()
{
int N;
cin>>N;
for(int i=0;i<N;i++)
scanf("%lf%lf",&P[i].x,&P[i].y);
int M=Graham(P,Res,N);
Print(Res,M);
return 0;
}
POJ2187可暴力可旋转卡壳
