【Notes_5】现代图形学入门——着色(光照模型、着色频率、重心坐标)

跟着闫令琪老师的课程学习，总结自己学习到的知识点

课程网址GAMES101
B站课程地址GAMES101
课程资料百度网盘【提取码：0000】

光栅化
- 着色（Shading）
  - Bling-Phong Reflection Model
- 着色频率

光栅化

着色（Shading）

在图形学中，着色的定义可以为：对物体(模型)应用某种材质。
主要是通过光照以及着色点参数进行表现。
在我们感知观察中，光线可以分为：高光、漫反射、环境光。

下面介绍一种简单的模型，对各种光照模型进行研究。

Bling-Phong Reflection Model

Phong反射模型

下图是光线照射到着色点上的示意图，为了便于分析，我们假设光线是从着色点方向发出。

Diffuse Reflection(漫反射)

漫反射： 当Phong模型表面是粗糙材质时，光照射到着色点时，会发生均匀反射，并且反射的光线的光强都相同。

那么每个入射的光线实际上照射到着色点的光强该怎么算。看下面的模型，首先光线与法线$n$的夹角 $\theta$有关，$\cos(\theta)=\vec{l}\cdot \vec{n}$，$(\vec{l} 、\vec{n})$为单位向量。

其次，图中中心为一个点光源，光线均匀的向周围发射，可以想象光源发射出来的能量其实是一定的，那么在任意两个圈上接受到的能量一定相等。而离圆心越远，圆的面积越大，单位面积所接受能量也就越弱。半径$r$上的一点接收的能量为$\frac{I}{r^2}$.

所以Diffuse Reflection可以用下面的式子表示

可以看出光强$L_d$与着色点表面参数$k_d$、入射角$max(0,\vec{n} \cdot \vec{l})$、入射时的光强$\frac{I}{r^2}$有关。

[Notes]: 入射角$max(0,\vec{n} \cdot \vec{l})$ 最小为0。

下图反应了着色点的表面参数对Diffuse Reflection的影响。

Specular HighLight(高光)

高光发生的反射实际上是镜面反射,所以反射光线的范围很小。所以想要表示Specular Trem，需要表示反射光线与视点观测线之间的远近。

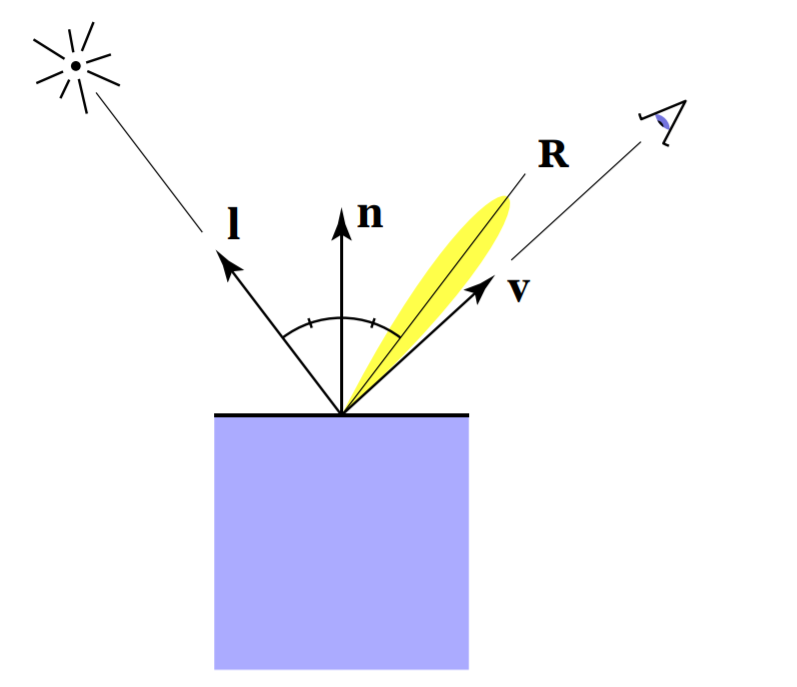
表示反射光线与视点观测线之间远近我们可以转化为求法线$\vec{n}$与半程向量$\vec{h}$之间的距离的远近。Specture Term也可以表示如下，仔细与Diffuse Term比较发现，Specture Term的相邻角是$max(0,\cos \alpha)^p$，多了个指数。原因【图2】,镜面反射的范围通常小，所以增加指数，这样，可以很好模拟镜面反射范围小。

由Specture Term可以知道镜面反射光强与镜面反射点参数$k_s$、入射时的光强$\frac{I}{r^2}$、视点与反射光线远近相关$max(0,\cos(\alpha))^p$有关。下图是$k_s、p$的对Specture HighLight的影响。

Ambient Term

环境光比较特殊、只有着色点表面因素的影响。

Blinn-Phong Reflection Model Term

基于以上三个式子，Bling-Phong模型的光照模型就可以表述出来了。

着色频率

前面我们知道了局部光照模型等式，但想要计算整个模型的光照模型，还需要知道每个模型上着色点的分布，引出了着色频率的概念。着色频率分为以下三种：Flat Shading、Gouraud Shading、Phong Shading，分别对应着三角形面着色、三角形顶点着色、每个点着色，以下是三种着色频率的效果。