Path Queries

G. Path Queries

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a weighted tree consisting of nn vertices. Recall that a tree is a connected graph without cycles. Vertices uiui and vivi are connected by an edge with weight wiwi.

You are given mm queries. The ii-th query is given as an integer qiqi. In this query you need to calculate the number of pairs of vertices (u,v)(u,v)(u<vu<v) such that the maximum weight of an edge on a simple path between uu and vv doesn't exceed qiqi.

Input

The first line of the input contains two integers nn and mm (1≤n,m≤2⋅1051≤n,m≤2⋅105) — the number of vertices in the tree and the number of queries.

Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by three integers uiui, vivi and wiwi — the labels of vertices it connects (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi) and the weight of the edge (1≤wi≤2⋅1051≤wi≤2⋅105). It is guaranteed that the given edges form a tree.

The last line of the input contains mm integers q1,q2,…,qmq1,q2,…,qm (1≤qi≤2⋅1051≤qi≤2⋅105), where qiqi is the maximum weight of an edge in the ii-th query.

Output

Print mm integers — the answers to the queries. The ii-th value should be equal to the number of pairs of vertices (u,v)(u,v) (u<vu<v) such that the maximum weight of an edge on a simple path between uu and vv doesn't exceed qiqi.

Queries are numbered from 11 to mm in the order of the input.

Examples

input

Copy

7 5
1 2 1
3 2 3
2 4 1
4 5 2
5 7 4
3 6 2
5 2 3 4 1

output

Copy

21 7 15 21 3 

input

Copy

1 2
1 2

output

Copy

0 0 

input

Copy

3 3
1 2 1
2 3 2
1 3 2

output

Copy

1 3 3 

Note

The picture shows the tree from the first example: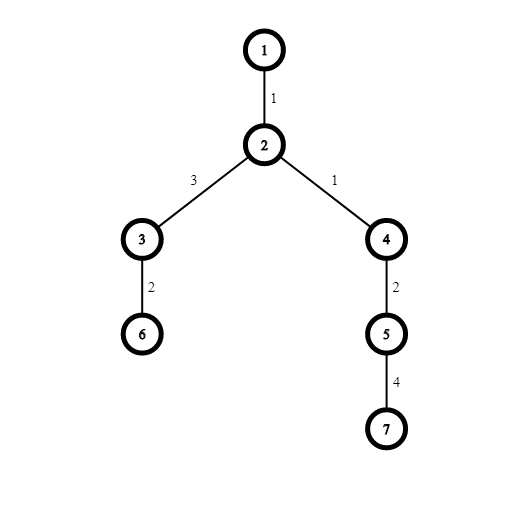

 

#pragma GCC optimize(2)

#include <bits/stdc++.h>

using namespace std;
const int maxn = 1e6 + 108;
typedef long long ll;
struct atom{
    int u,v,w;
    bool operator<(const atom& cur)const {
        return w<cur.w;
    }
}o[maxn];
int n,m,fa[maxn];
ll num[maxn],res[maxn];

inline int getfa(int cur){
    return cur==fa[cur]?cur:fa[cur]=getfa(fa[cur]);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("1.txt", "r", stdin);
#endif
    scanf("%d%d",&n,&m);
    for(register int i=1;i<=n;++i){
        fa[i]=i;
        num[i]=1;
    }
    for(register int i=1;i<n;++i){
        scanf("%d%d%d",&o[i].u,&o[i].v,&o[i].w);
    }
    sort(o+1,o+n);
    for(register int i=1;i<n;++i){
        int fu=getfa(o[i].u);
        int fv=getfa(o[i].v);
        res[o[i].w]+=num[fu]*num[fv];
        num[fu]+=num[fv];
        fa[fv]=fu;
    }
    for(register int i=1;i<=360000;++i){
        res[i]=res[i]+res[i-1];
        //printf("debug res[%d] = %d\n",i,res[i]);
    }
    int query;
    while(m--){
        scanf("%d",&query);
        printf("%lld ",res[query]);
    }
    return 0;
}