医院设置（图论Floyd）

问题 A: 【图】

[提交] [状态] [讨论版] [命题人:admin]

题目描述

设有一棵二叉树，如图：

 

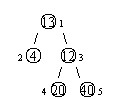其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为l。如上图中，

若医院建在1 处，则距离和=4+12+2*20+2*40=136；若医院建在3 处，则距离和=4*2+13+20+40=81……

 

输入

第一行一个整数n，表示树的结点数。(n≤100)

接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格(一个或多个)分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接。

 

输出

一个整数，表示最小距离和。

 

样例输入

复制样例数据

5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

样例输出

81
思路：Floyd跑出最短路，再枚举医院的位置。

#include<bits/stdc++.h>
using namespace std;
int n, dp[105][105],p[105],ans;
#define REP(i, a, b) for(int i = (a); i <= (b); ++ i)
#define REP(j, a, b) for(int j = (a); j <= (b); ++ j)
#define PER(i, a, b) for(int i = (a); i >= (b); -- i)
template <class T>
inline void rd(T &ret) {
    char c;
    ret = 0;
    while ((c = getchar()) < '0' || c > '9');
    while (c >= '0' && c <= '9') {
        ret = ret * 10 + (c - '0'), c = getchar();
    }
}
int main() {
    rd(n);
    ans = 0x3f3f3f3f;
    REP(i, 1, n) {
        REP(j, 1, n) {
            dp[i][j] = 0x3f3f3f3f;
        }
    }
    REP(i, 1, n) {
        int y, z;
        rd(p[i]),rd(y), rd(z);
        if (y)dp[i][y] = dp[y][i]=1;
        if (z)dp[i][z] = dp[z][i] = 1;
        dp[i][i] = 0;
    }
    for (int k = 1; k <= n; k++) {
        REP(i, 1, n) {
            REP(j, 1, n) {
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
            }
        }
    }
    REP(i, 1, n) {
        int cur = 0;
        REP(j, 1, n) {
            cur += dp[i][j] * p[j];
        }
        ans = min(ans, cur);
    }
    cout << ans << endl;
}