[题解] [笔记] 可反悔贪心 & lgP3620|lgP1484|lgP1792
[题解] [笔记] 可反悔贪心 & \(lgP3620|lgP1484|lgP1792\)
写在前面
我们以\(lgP1484\)为例。
在考场上,我写了一个\(DP(50pts)\),先放一下代码,虽然不是正解但和正解的思路有异曲同工之妙相同之处。
#include <bits/stdc++.h>
using namespace std;
long long val[500010];
long long f[2][500010][2];
int main(){
freopen("prob.in","r",stdin);
freopen("prob.out","w",stdout);
int n,k;
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;i++){
scanf("%lld",&val[i]);
}
int x = 1;
for(int i = 1;i <= n;i++){
for(int j = k;j >= 1;j--){
f[x][j][0] = max(f[x ^ 1][j][0],f[x ^ 1][j][1]);//如果当前不种就可以从前一棵树继承信息
f[x][j][1] = f[x ^ 1][j - 1][0] + val[i];//当前要种树那么只能从前一个坑中没有种树的状态转移
}
x ^= 1;
}
x ^= 1;//最后一次循环的时候x的值变了但是没有对应的f数组的值,所以统计答案的时候要用最后一次有值的来当作答案
long long maxx = 0;
for(int i = 1;i <= k;i++){
maxx = max(maxx,f[x][i][0]);
maxx = max(maxx,f[x][i][1]);
}
printf("%lld\n",maxx);
}
\(f[i][j][0/1]\)表示的是当前判断种或不种第\(i\)棵树,\(j\)表示的是已经种了\(j\)棵树,最后一维\(0\)表示不种,\(1\)表示种。
然后有关异或的操作是滚动数组的实现,为了节省空间。
算法介绍
过程描述
那么这道题正解用的方法是贪心+双向链表。
首先假设我们有\(4\)个树坑,种\(2\)棵树,树的价值分别为:\(8,9,8,2\)。
如果我们直接贪心的话肯定是选第一个和第三个(因为不能连着种),但是显然我们发现选第二个和第四个会更优。那怎么解决这个问题呢?
我们可以对于每个点建立双向链表,并把每个点用大根堆来维护,具体的方法是:每次弹出堆顶没有被访问过的元素(必定是当前价值最大的),接着让答案加上这个点的权值,把这个点的左右两个点标记为已经访问过,最关键的是,还要往大根堆里插入一个点:这个点的权值是当前点左右两个点的权值和减去当前点的权值。可以结合上面的\(DP\)思路来理解。
上面的过程如图所示: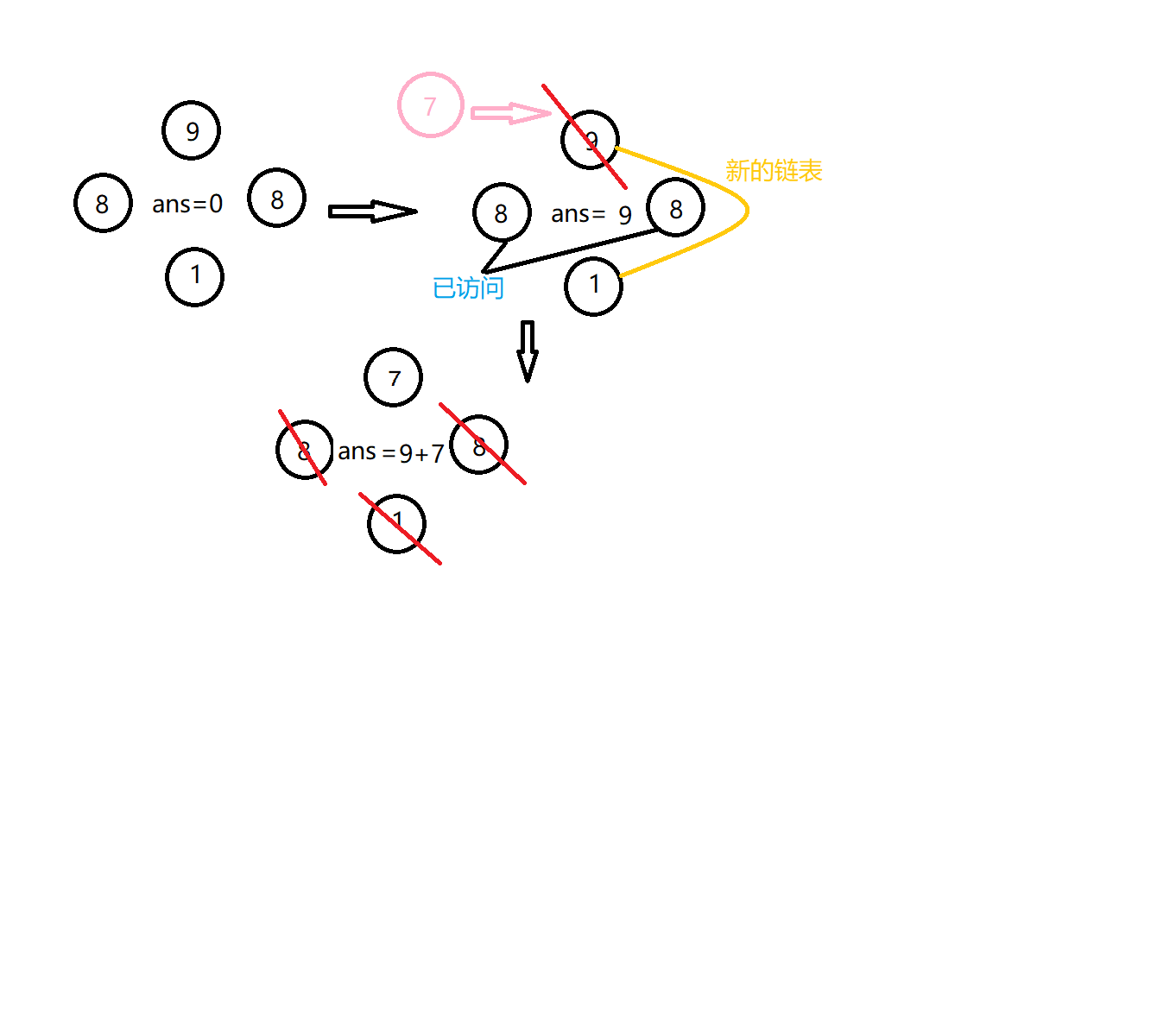
为什么这样是对的呢?这样做的过程其实是建立了一个可以反悔的状态。每次选完一个点就要插入一个点权为当前点左右两个点的权值和减去当前点的权值的点,这个代表的意思其实就是不选当前这个点可以得到的另一种答案。而在上面举的例子中选\(9\)这个点之后其实是需要反悔的,而过程就是:首先把一开始的\(4\)个点全部插入大根堆,那么第一个弹出并且没有访问的点就是\(9\),此时答案变成\(9\),把\(9\)这个点两边的点标记为已经访问,但\(9\)本身这个位置不用标记为已访问因为之后还要插入新节点,在原来\(9\)所在的位置插入权值为\(8+8-9=7\)的点,并且更新链表,把\(7\)连到\(1\),因为它原本的左右两边的点已经被访问过了。此时大根堆中的点是:\(8,8,7,1\),弹出两个\(8\)因为已经访问过了,此时再弹出的就是\(7\),没有访问过,所以答案累加\(7\)变成\(16\),此时已经种完了要种的\(2\)棵树,可以退出了。
算法原理(正确性)
那么这个可反悔的贪心就在于本身答案应该是\(8+8=16\),但是在程序实现的过程中却变成了\(9+7=16\),我们发现答案并没有变化,为什么呢?其实我们在累加\(9\)和\(7\)的时候其实是加\(9+8+8-9=16\),所以其实一个点选完之后可以被在它位置上新插入的点消除影响,也就是说如果一个点(比如例题中的\(9\))不是最优的但是被选中了,此时在被选中节点新插入的节点(例题中的\(7\))可以支持反悔(这里支持反悔的意思是可以把答案中之前加的\(9\)去掉,改为累加原来\(9\)左右的两个点),也就是不选之前选的不优的点,改为选它两边(例题中的两个\(8\)节点)的点。
代码
注意
这几道题的算法完全一样思路也是,不同就在于一些细节比如首尾能不能相接,是要最大值还是最小值之类,比较好理解,就不多说
\(lgP1484\)
#include <bits/stdc++.h>
using namespace std;
struct node{
long long val,id;
bool operator < (const node &a)const{
return a.val > val;
}
};
struct tree{
long long val,l,r;
}tr[500010];
priority_queue < node > q;
bool vis[500010];
int n,m;
long long ans;
void rebuild(int x){
tr[x].l = tr[tr[x].l].l;
tr[x].r = tr[tr[x].r].r;
tr[tr[x].l].r = x;
tr[tr[x].r].l = x;
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++){
scanf("%lld",&tr[i].val);
tr[i].l = i - 1;
tr[i].r = i + 1;
q.push((node){tr[i].val,i});
}
for(int i = 1;i <= m;i++){
while(vis[q.top().id])q.pop();
node now = q.top();
q.pop();
if(now.val <= 0)break;
ans += now.val;
vis[tr[now.id].l] = vis[tr[now.id].r] = true;
tr[now.id].val = tr[tr[now.id].l].val + tr[tr[now.id].r].val - tr[now.id].val;
q.push((node){tr[now.id].val,now.id});
rebuild(now.id);
}
printf("%lld\n",ans);
return 0;
}
\(lgP1792\)
#include <bits/stdc++.h>
using namespace std;
struct node{
int val,id;
bool operator < (const node &a)const{
return a.val > val;
}
};
struct tree{
int val,l,r;
}tr[200010];
priority_queue < node > q;
bool vis[200010];
int n,m,ans;
void rebuild(int x){
tr[x].l = tr[tr[x].l].l;
tr[x].r = tr[tr[x].r].r;
tr[tr[x].l].r = x;
tr[tr[x].r].l = x;
}
int main(){
scanf("%d%d",&n,&m);
if(n < m * 2){
printf("Error!\n");
return 0;
}
for(int i = 1;i <= n;i++){
scanf("%d",&tr[i].val);
tr[i].l = i - 1;
tr[i].r = i + 1;q.push((node){tr[i].val,i});
}
tr[1].l = n;tr[n].r = 1;
for(int i = 1;i <= m;i++){
while(vis[q.top().id])q.pop();
node now = q.top();
q.pop();
ans += now.val;
vis[tr[now.id].l] = vis[tr[now.id].r] = true;
tr[now.id].val = tr[tr[now.id].l].val + tr[tr[now.id].r].val - tr[now.id].val;
q.push((node){tr[now.id].val,now.id});
rebuild(now.id);
}
printf("%d\n",ans);
return 0;
}
\(lgP3620\)
#include <bits/stdc++.h>
using namespace std;
struct node{
long long val,id;
bool operator < (const node &a)const{
return a.val < val;
}
};
struct tree{
long long val,l,r;
}tr[500010];
priority_queue < node > q;
bool vis[500010];
int n,m,last;
long long ans;
void rebuild(int x){
tr[x].l = tr[tr[x].l].l;
tr[x].r = tr[tr[x].r].r;
tr[tr[x].l].r = x;
tr[tr[x].r].l = x;
}
int main(){
scanf("%d%d%d",&n,&m,&last);
for(int i = 1;i < n;i++){
int x;
scanf("%d",&x);
tr[i].val = x - last;
last = x;
tr[i].l = i - 1;
tr[i].r = i + 1;
q.push((node){tr[i].val,i});
}
tr[0].val = tr[n].val = 1e9;
for(int i = 1;i <= m;i++){
while(vis[q.top().id])q.pop();
node now = q.top();
q.pop();
ans += now.val;
vis[tr[now.id].l] = vis[tr[now.id].r] = true;
tr[now.id].val = tr[tr[now.id].l].val + tr[tr[now.id].r].val - tr[now.id].val;
q.push((node){tr[now.id].val,now.id});
rebuild(now.id);
}
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号