[笔记][题解]树链剖分&lgP3384
[笔记]树链剖分
算法概述
树链剖分就是把一棵树分成几条不相交的链来做.
变量定义
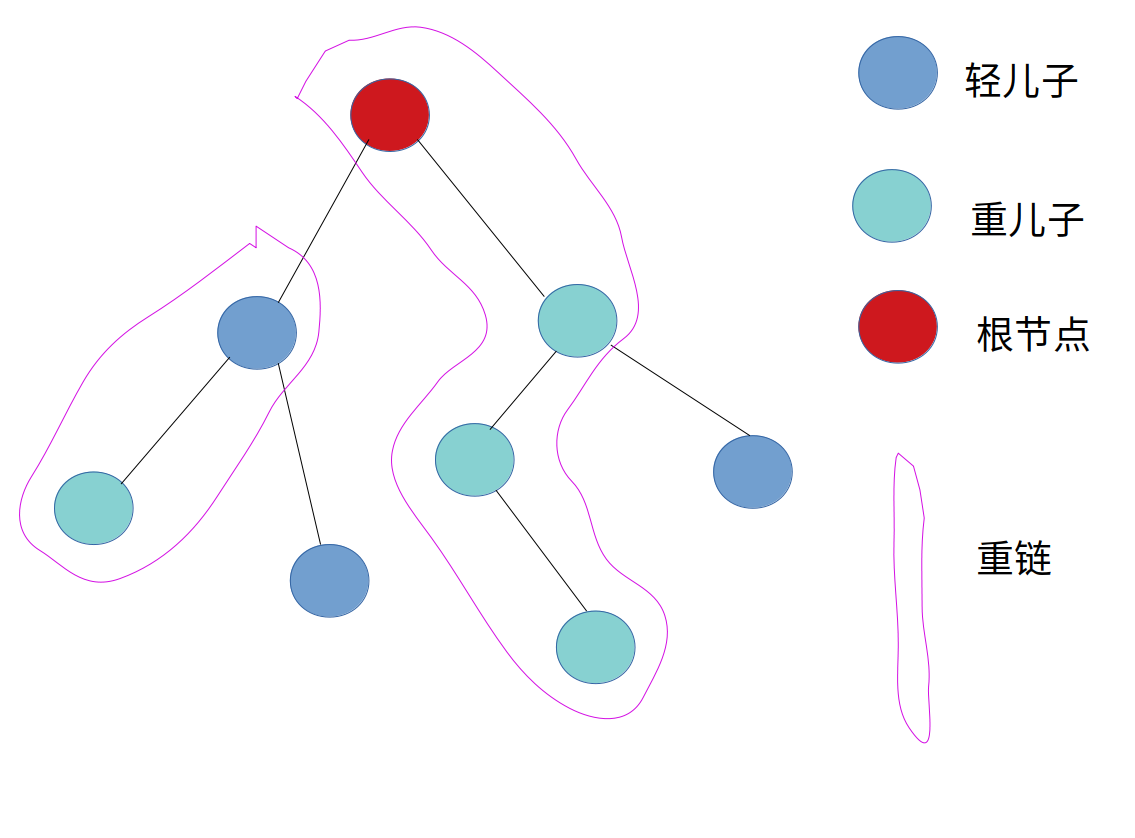
重儿子:某个节点(非叶子节点)的子树中,节点个数最多的子树的根节点(即与这个点相连的点)就是这个点的重儿子.
轻儿子:对于一个非叶子节点,它的儿子中非重儿子的剩下所有儿子就是轻儿子,也就是说叶子节点没有轻儿子或重儿子.
重边:连接某个节点和它的重儿子的边
重链:由许多重边所构成的链
轻链:由许多非重边构成的链
这样,对于一个节点,找出了它的重儿子,这棵树就被自然的拆成了许多重链和轻链.
算法详述
·显然,我们需要维护这些链,那么就要对所有链上的点用\(dfs\)进行重新编号.
dfs1
task:
1.标记每个点的深度dep[i];
2.标记每个点的父亲fa[i];
3.标记每个非叶子节点的字数大小(包含根节点).
4.标记每个非叶子节点的重儿子编号son[i].
void dfs1(int x,int f,int depth){//x为当前节点,f为爸爸,depth为深度
dep[x] = depth;
fa[x] = f;
size[x] = 1;//包含自己的儿子的个数
int heavyson_size = -1;//记录重儿子的儿子个数
for(int i = fir[x];i;i = edge[i].next){
if(edge[i].to == f)continue;//如果搜到的是父亲就跳过
dfs1(edge[i].to,x,dep + 1);
size[x] += size[edge[i].to];
if(size[edge[i].to] > heavyson_size){
son[x] = edge[i].to;
heavyson_size = size[edge[i].to];
}
}
}
dfs2
task:
1.标记每个点的新编号
2.将每个点的初始值赋给新的编号上
3.处理每个点所在链的顶端
4.处理每条链
注意:这里要先处理重儿子再处理轻儿子,因为在标新标号时是重儿子优先的.标号如图

同时我们可以发现,由于是进行\(dfs\),所以每一个子树的编号是连续的
void dfs2(int x,int topp){//topp是当前链的最顶端的节点
id[x] = ++cnt;//新的编号
wt[cnt] = w[x];//把当前点的初值赋给新的编号
if(!son[x])return;//如果没有重儿子就返回
dfs2(son[x],topp);//要先处理重儿子
for(int i = fir[x];i;i = edge[i].next){
if(edge[i].to == fa[x] || edge[i].to == son[x])//如果搜到了重儿子就跳过,因为在之前就搜过了.
continue;
dfs2(y,y);//每个轻儿子都有一条从自己开始的轻链
}
}
解决问题
一.处理任意两点间路径上的点权和
1.设所在链的链顶深度更深的那个点为\(x\),\(ans\)加上\(x\)点到\(x\)所在链顶端这一段区间的点权和.
2.把\(x\)调到\(x\)所在链顶端的那个点的父亲节点.
3.重复一上步骤,直到两个点在同一条链上
代码实现:
int res;
int ask_range(int x,int y){
int ans = 0;
while(top[x] != top[y]){//两个点不在同一条链上.
if(dep[top[x]] < dep[top[y]])swap(x,y);//意思是上面的第1步.
res = 0;
ask(1,1,n,id[top[x]],id[x]);//求到链顶的这一段区间的点权和.
ans += res;ans %= mod;
x = fa[top[x]];//意思是上述的第2步.
}
//现在连个点都在同一条链上.
if(dep[x] > dep[y])swap(x,y);
res = 0;
ask(1,1,n,id[x],id[y]);//加上连个点之间的点权和.
}
二.处理一个点及它子树的点权和
比较简单,因为每个子树的编号都是连续的.
所以,如果某个子树的根节点是\(x\),那么这个子树的编号左端点就是id[x],右端点就是id[x] + size[x] - 1.
代码:
int ask_son(int x){
res = 0;
ask(1,1,n,id[x],id[x] + size[x] - 1);
return res;
}
三.区间修改
类似于线段树,与问题一差不多.
void change_range(int x,int y,int k){//区间修改
k %= mod;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
change(1,1,n,id[top[x]],id[x],k);
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
change(1,1,n,id[x],id[y],k)
}
void change_son(int x,int k){//修改子树
change(1,1,n,id[x],id[x] + size[x] - 1,k);
}
到这里,树链剖分的基本用途和实现就讲完了,放上完整代码:
#include <bits/stdc++.h>
using namespace std;
struct node{
int to,next;
}edge[1000010 * 4];
struct seg_tree{
int l,r,tag,w;
}tree[1000010 * 4];
int fir[1000010],tot,root;
int n,m,r,mod,w[1000010];
int dep[1000010],res,fa[1000010],top[1000010],son[1000010];
int wt[1000010],id[1000010],size[1000010],cnt;
void pushdown(int num){
tree[num * 2].tag += tree[num].tag;
tree[num * 2 + 1].tag += tree[num].tag;
tree[num * 2].w += tree[num].tag * (tree[num * 2].r - tree[num * 2].l + 1);
tree[num * 2 + 1].w += tree[num].tag * (tree[num * 2 + 1].r - tree[num * 2 + 1].l + 1);
tree[num * 2].w %= mod;
tree[num * 2 + 1].w %= mod;
tree[num].tag = 0;
}
void add(int x,int y){
edge[++tot].to = y;
edge[tot].next = fir[x];
fir[x] = tot;
return;
}
void build(int num,int l,int r){
tree[num].l = l;tree[num].r = r;tree[num].tag = 0;
if(l == r){
tree[num].w = wt[l];
tree[num].w %= mod;
return;
}
int mid = (l + r) / 2;
build(num * 2,l,mid);
build(num * 2 + 1,mid + 1,r);
tree[num].w = tree[num * 2].w + tree[num * 2 + 1].w;
tree[num].w %= mod;
}
void ask(int num,int tar_l,int tar_r){
if(tree[num].l >= tar_l && tree[num].r <= tar_r){
res += tree[num].w;
res %= mod;
return;
}
pushdown(num);
int mid = (tree[num].l + tree[num].r) / 2;
if(tar_l <= mid)
ask(num * 2,tar_l,tar_r);
if(tar_r > mid)
ask(num * 2 + 1,tar_l,tar_r);
}
void change(int num,int tar_l,int tar_r,int k){
if(tree[num].l >= tar_l && tree[num].r <= tar_r){
tree[num].tag += k;
tree[num].w += k * (tree[num].r - tree[num].l + 1);
tree[num].w %= mod;
return;
}
pushdown(num);
int mid = (tree[num].l + tree[num].r) / 2;
if(tar_l <= mid)
change(num * 2,tar_l,tar_r,k);
if(mid < tar_r)
change(num * 2 + 1,tar_l,tar_r,k);
tree[num].w = tree[num * 2].w + tree[num * 2 + 1].w;
tree[num].w %= mod;
}
int ask_range(int x,int y){
int ans = 0;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
res = 0;
ask(1,id[top[x]],id[x]);
ans += res;
ans %= mod;
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
res = 0;
ask(1,id[x],id[y]);
ans += res;
ans %= mod;
return ans;
}
void change_range(int x,int y,int k){
k %= mod;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
change(1,id[top[x]],id[x],k);
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
change(1,id[x],id[y],k);
}
int ask_son(int x){
res = 0;
ask(1,id[x],id[x] + size[x] - 1);
return res;
}
void change_son(int x,int k){
change(1,id[x],id[x] + size[x] - 1,k);
}
void dfs1(int x,int f,int depth){
dep[x] = depth;
fa[x] = f;
size[x] = 1;
int heavyson_size = -1;
for(int i = fir[x];i;i = edge[i].next){
if(edge[i].to == f)continue;
dfs1(edge[i].to,x,depth + 1);
size[x] += size[edge[i].to];
if(size[edge[i].to] > heavyson_size){
heavyson_size = size[edge[i].to];
son[x] = edge[i].to;
}
}
}
void dfs2(int x,int topp){
id[x] = ++cnt;
wt[cnt] = w[x];
top[x] = topp;
if(!son[x])return;
dfs2(son[x],topp);
for(int i = fir[x];i;i = edge[i].next){
if(edge[i].to == fa[x] || edge[i].to == son[x])continue;
dfs2(edge[i].to,edge[i].to);
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&root,&mod);
for(int i = 1;i <= n;i++)scanf("%d",&w[i]);
for(int i = 1;i < n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
dfs1(root,0,1);
dfs2(root,root);
build(1,1,n);
while(m--){
int k,x,y,z;
scanf("%d",&k);
if(k == 1){
scanf("%d%d%d",&x,&y,&z);
change_range(x,y,z);
}
else if(k == 2){
scanf("%d%d",&x,&y);
printf("%d\n",ask_range(x,y));
}
else if(k == 3){
scanf("%d%d",&x,&y);
change_son(x,y);
}
else{
int x;
scanf("%d",&x);
printf("%d\n",ask_son(x));
}
}
return 0;
}


