1.学习总结(2分)
1.1图的思维导图
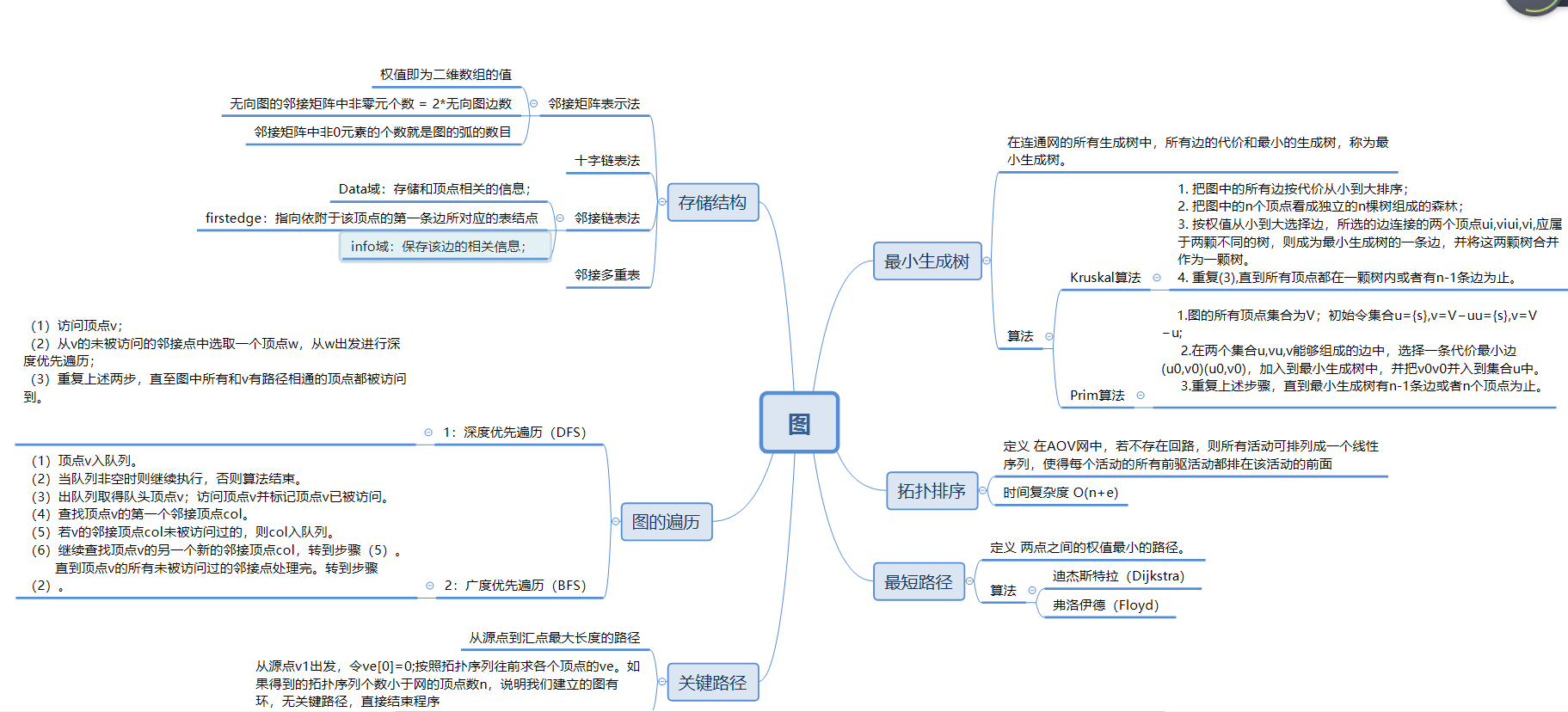
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
在这次的图结构学习中收获很多,首先是遍历的方法的学习,一个是深度优先遍历一个是广度遍历,
两种遍历各有各的优势,取决于题目的要求,例如pta的图着色问题我觉得使用广度优先遍历比较好,
两种算法各有所长。
Prim算法和Kruskal算法都是贪心算法,关于最小生成树的建立,两者都是很优秀的算法,,prim由
于要用到邻接矩阵,所以稠密图比较合适,kruskal要对所有的边排序,因此稀疏图比较合适。
所以采取那种算法可以取决是稠密图还是稀疏图来选择算法。
Dijkstra算法也是采用贪心算法的策略,但是他多了一个数组dist来保存最短路径,并经过不断的修改来达到
计算各个点的最小路径的目的。所以学会这个算法关键还是在于修改的这个过程。
拓扑排序算法在我的理解中也是对于图的遍历只不过在于它要求要有入度为0的点来遍历,因此关键
点就是找这个入度为0的点,再就是怎么定义入度,怎么修改入度都是很关键的点,采用栈来解决就很好
地可以处理这类问题。
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题(25 分)
2.2 设计思路(伪代码或流程图)
定义全局变量 flag判断方案成功的标志
定义 n e z f分别定义点数、边数、颜色数及操作数
定义 字符串a
输入n z e的值
CreateMGraph(g,n,e )//建图我在这里省略,我是用邻接矩阵建图
输入f的值
while(f--)
{
定义数组c[501] 存放颜色的分配方案 b[500]存放颜色出现的个数 sum存放总的颜色数
for i=1 to i=g.n
输入颜色的方案与c[i]中
记录颜色的次数b[c[i]]
记录总的颜色数sum
end for
if(sum等于规定的颜色数z)
flag=0
else
进入二次循环判断每一节点相邻的颜色c[i]与c[j]是否相同
若是flag=0否则flag=1
if(flag为0)
输出 No
否则
输出 Yes
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
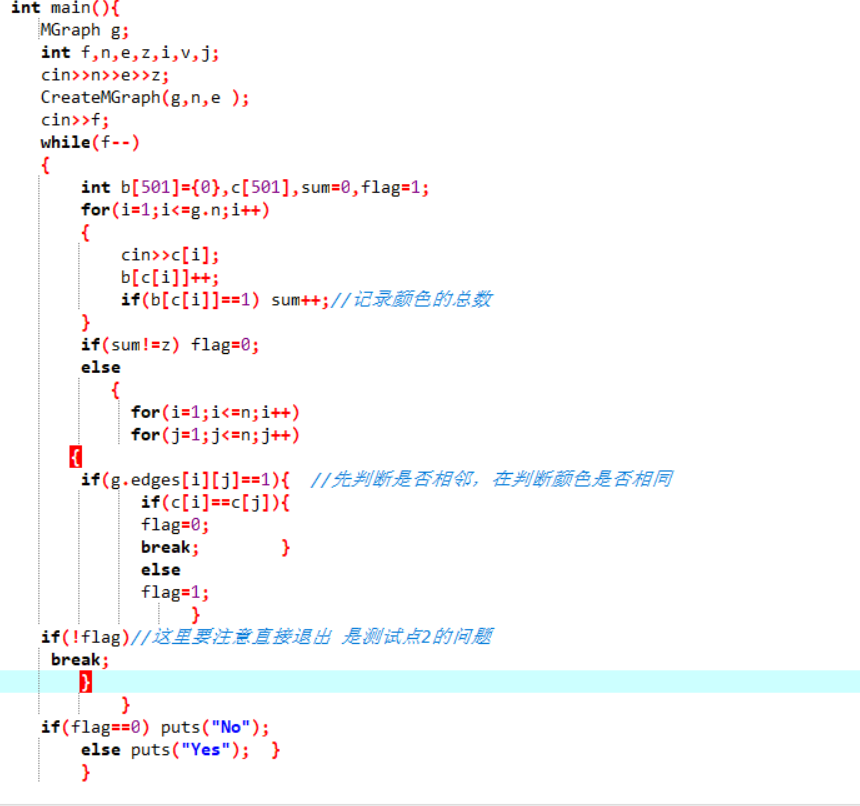
2.4 PTA提交列表说明。
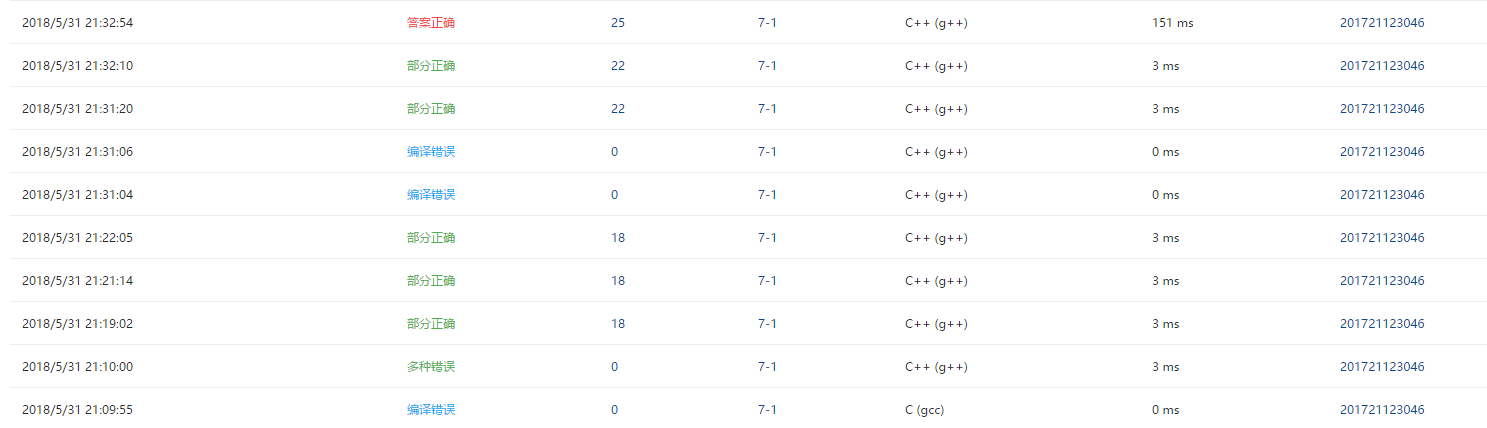
- 做这道题的时候我遇到两个问题,第一个比较简单是因为图的大小设置过小,导致最大图出现段错误,还有一个问题是第二个测试点 卡DFS不重复访问顶点的错误
出现错误,我用自己的数据测试了一下发现是判断的时候出现错误,因为我没有使用DFS,所以我看了一下我的代码,才发现是在判断相邻的点时一旦发现颜色相同
就应该退出判断,不必继续判断导致错误。
2.1 题目2:7-3 六度空间(30 分)
2.2 设计思路(伪代码或流程图)
核心内容是广度遍历,我对广度函数遍历修改来做这道题,所以这里展示的是我该后的函数
int BFS(int v){
定义队列数组q[10002],头位置f=0,尾位置r=0,计数count=0 ,层级level=0,层最后的位置last,w,de
for i=1 to n
将visited[i]初始化为0
end for
visited[v]=1
将v进队q
while(q不为空)
将q出队置于于w中
for i=1 to n
if(w与i相邻且i未被访问)
visited[i]=1;
count++;
将i进队
记录该层最后的位置tail
end if
end for
if(w等于last)
层数加一
last=tail
if(level等于6)
break
end while
return count
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
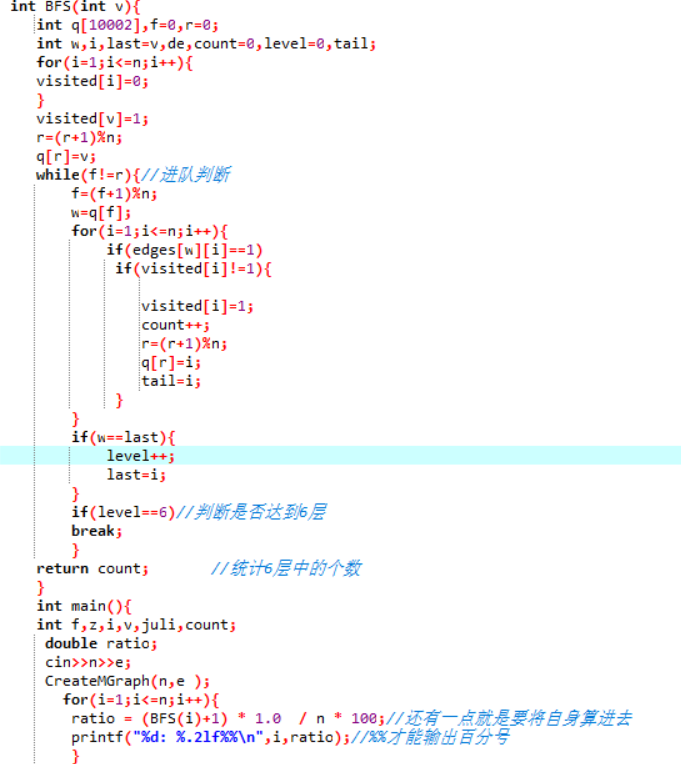
2.4 PTA提交列表说明。

- 这道题我遇到的问题是使用结构体建图时,我最后一点最大的M和N一直过不了,总是段错误,后来我询问了一下舍友,他也遇到相同的问题
原来是结构体存储不了很大的二维数组,因为我们都是用领结矩阵建图的,所以我就改成了用一个全局变量来建立而没有使用结构体,后来在课上的
一位同学使用连接表来建图,这样可以大大减少空间的存储量,因为是稀疏图,原先我一直以为领结矩阵建图比较直观又简单,感觉领结表没用,现在
才发现各有所长。所以令我受益匪浅。
2.1 题目1:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
这道题是计算最小生成树的问题具体代码为修改后的prim函数代码
还有一个关键点是我在建图时将其初始化为66666
int Prim()
定义TotalCost = 0存放道路的长度, Vcount = 0存放边的个数, V, W;
for(V=1 to n)
初始化dist
dist[V] = edges[1][V]
end for
dist[1] = 0
边的个数Vcount加1
while(1)
V = FindMinDist()
边数Vcount加一;
计算TotalCost并将dist[v]收录
for W=1 to n
if(dist[W]不为0且V<->W之间的距离变小)
修改dist的值为edges[V][W]
end for
if(Vcount等于n)
return TotalCost;
else
return -1
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)


2.4 PTA提交列表说明。
- 这道题采用的是求最小的生成树的prim算法,遇到的问题是在判断联通与没有联通的时候那点的错误,
后来我改了一下把初始的值改为无穷的值即可解决,其他的就和书上的的算法差不多了。
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:255
4. 阅读代码(必做,1分)

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<sstream>
#include<cstring>
#include<cstdio>
#include<string>
#include<deque>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define INF 0x3f3f3f3f
#define MM(x) memset(x,0,sizeof(x))
using namespace std;
typedef long long LL;
const int N=10020;
typedef pair<int,double> psd;
vector<psd>E[1050];
double d[N];
int n,m,k;
double ds;
inline int bianhao(char s[])
{
int len=strlen(s);
int r=0;
if(s[0]=='G')
{
for (int i=1; i<len; i++)
r=r*10+(s[i]-'0');
return 1000+r;
}
else
{
for (int i=0; i<len; i++)
r=r*10+(s[i]-'0');
return r;
}
}
inline void spfa(const int &s,const int &t)
{
d[s]=0;
priority_queue<pair<double,int> >Q;
Q.push(pair<double,int>(-d[s],s));
while (!Q.empty())
{
int now=Q.top().second;
Q.pop();
for (int i=0; i<E[now].size(); i++)
{
int v=E[now][i].first;
if(d[v]>d[now]+E[now][i].second)
{
d[v]=d[now]+E[now][i].second;
Q.push(pair<double,int>(-d[v],v));
}
}
}
}
struct info
{
int s;
double aver,sum,minm;
info(const int &ss,const double &av,const double &su,const double &mm):s(ss),aver(av),sum(su),minm(mm){}
info(){}
};
bool cmp(const info &a,const info &b)
{
if(a.minm!=b.minm)
return a.minm>b.minm;//就是这个地方写成了a.minm>b.sum,强行WA数次- -
if(a.aver!=b.aver)
return a.aver<b.aver;
else
return a.s<b.s;
}
int main(void)
{
int i,j;
while (~scanf("%d%d%d%lf",&n,&m,&k,&ds))
{
for (i=0; i<1050; i++)
E[i].clear();
char s[5],t[5];
int S,T;
double dx;
for (i=0; i<k; i++)
{
scanf("%s%s%lf",s,t,&dx);
S=bianhao(s);
T=bianhao(t);
E[S].push_back(psd(T,dx));
E[T].push_back(psd(S,dx));
}
info ans[1000];int cnt=0;
for (i=1; i<=m; i++)
{
memset(d,0x43,sizeof(d));
for (j=1; j<=n; j++)
spfa(i+1000,j);
bool flag=1;
double sss=0,tj,mm=1e6;
for (j=1; j<=n; j++)
{
tj=d[j];
if(tj>ds)
{
flag=0;
break;
}
sss+=tj;
if(tj<mm)
mm=tj;
}
if(flag)
ans[cnt++]=info(i,sss/n,sss,mm);
}
if(cnt==0)
puts("No Solution");
else
{
sort(ans,ans+cnt,cmp);
printf("G%d\n%.1lf %.1lf\n",ans[0].s,ans[0].minm,ans[0].aver);
}
}
return 0;
}
- 这道题也是求最短路径的问题,刚开始题目意思比较难理解:“选在到所有居民点的最短距离最长的地方”。首先知道题目中对答案的限制条件只有一个,
那就是最大距离不能超过Ds,那么对在此基础上筛选下来的候选位置中计算他们各自的到所有居民区的最短距离,然后当然此前要对筛选出来的答案存放到数组,
然后排序一下。所以要加大了难度,
我找到的这篇代码使用了spfa函数计算路径,也是很好的方法。


 posted on
posted on

