1.学习总结(2分)
1.1树结构思维导图
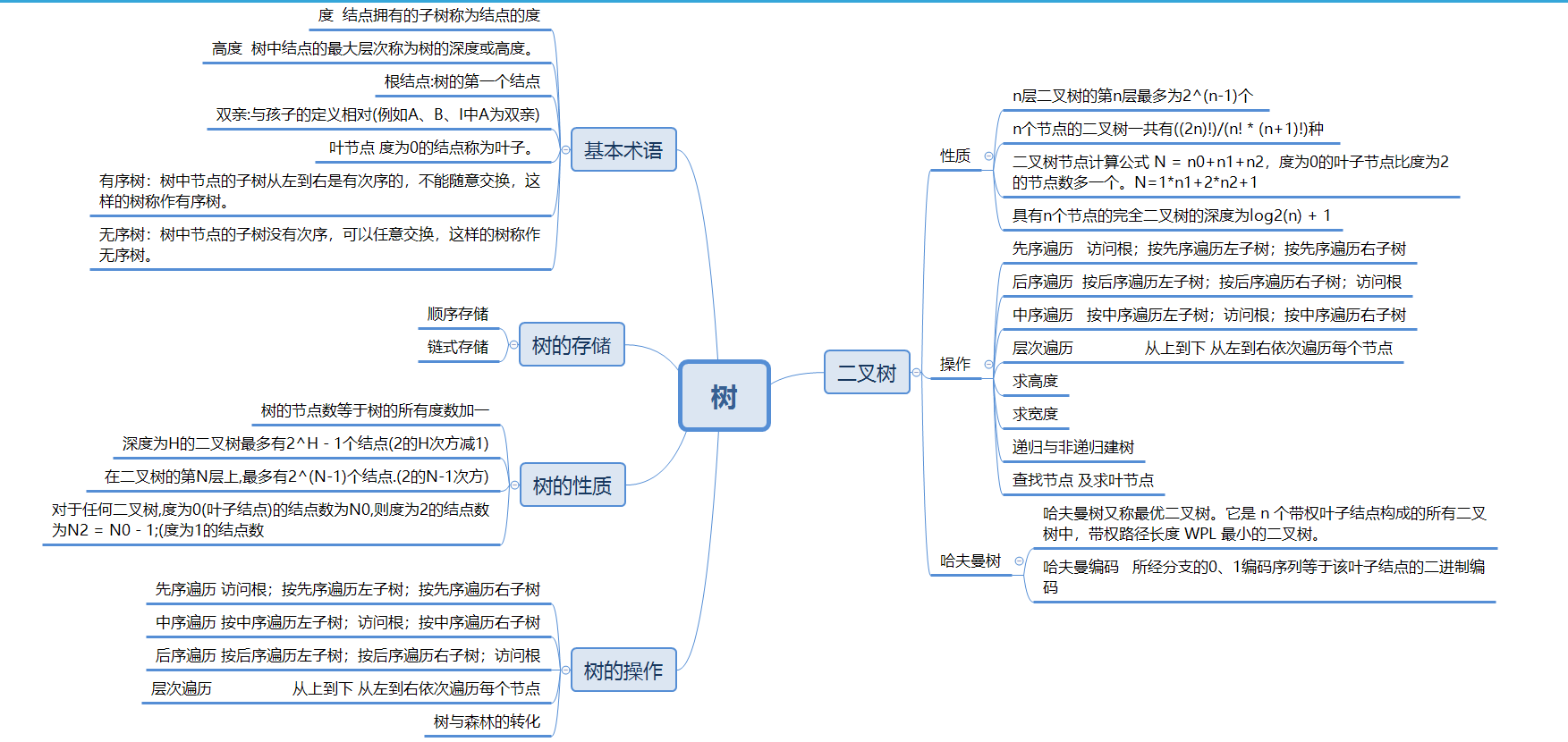
1.2 树结构学习体会
- 在学习完树后学到了很多也仍然有许多疑难杂症困扰着我,树的这种数据结构在处理很多问题的时候时间复杂度减少了很多,可以更方便的处理很多问题
比如查找树,哈夫曼树,等的应用。是一种处理数据的好方法。 - 遇到的困难 在学习树的时候我对于树的创建这一块比较难理解,首先递归建立代码简单但是思维比较复杂难理解,在编写程序时总是会有一些一些小失误,
例如这次上机考,再求宽度时,,就不会怎么处理。而非递归建立的话借助队列或者栈来建立,代码量大右很复杂。还有就是在哈夫曼树的理解不是很透测,
因为题目没涉及,还需要加强。
2.PTA实验作业(4分)
2.1 题目1:6-2 求二叉树高度
2.2 设计思路(伪代码或流程图)
int GetHeight( BinTree BT )
定义 lchildh,rchildh分别存储左右树的高度
if(树为空)
return 0
else
比较 lchildh,rchildh哪个大return哪个
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
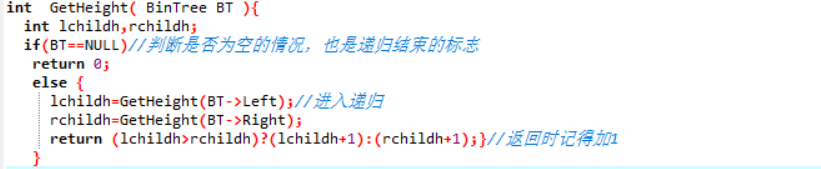
2.4 PTA提交列表说明。
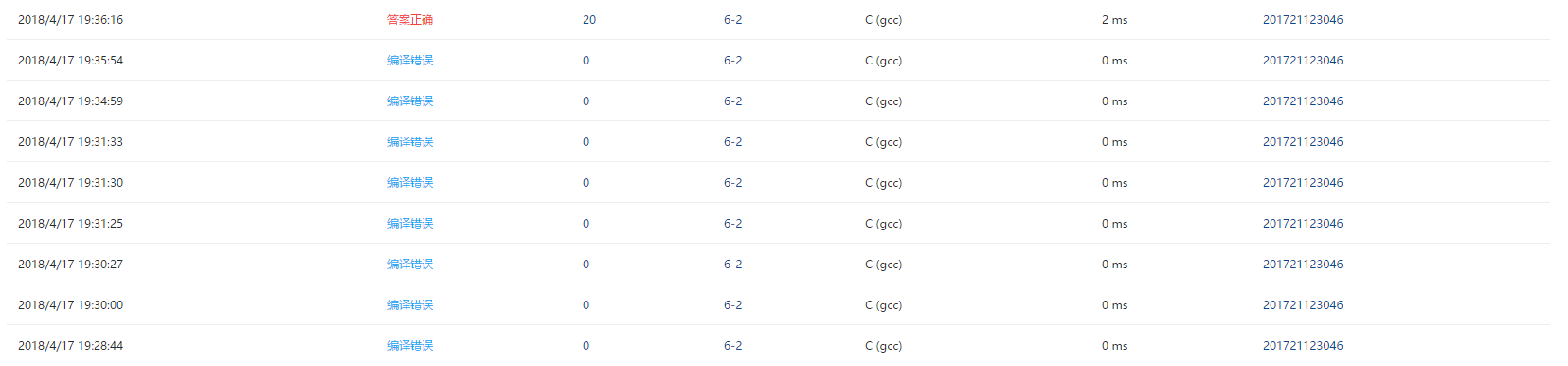
- 这题主要是递归的代码没搞清楚导致编译错误,其余还是比较简单的。
2.1 题目2:6-4 jmu-ds-表达式树
2.2 设计思路(伪代码或流程图)
void InitExpTree(BTree &T,string str) 建树
定义一个运算符栈s和一个操作数树节点栈stacktree
先将#入s栈
for(字符串str未结束)
if(str为运算符){
while(s的栈顶优先级大于str)
创建一个树节点T,数据为s.top()
stacktree弹出两个是数据分别放入T->lchild T->rchild
stacktree.push(T)
end while
if(s的栈顶优先级小于str)
s.push(str)
if(s的栈顶优先级等于str)
s.pop()
}
else {
创建一个树节点T,数据为str
T->lchild T->rchild均为NULL
stacktree.push(T)
}
end for
while(s的栈顶不为#)
创建一个树节点T,数据为s.top()
stacktree弹出两个是数据分别放入T->lchild T->rchild
stacktree.push(T)
end
T=stacktree.top()
double EvaluateExTree(BTree T)计算树
定义节点栈s 及计算值栈s1
定义 a b result 存放操作数及结果 flag=-1
先将T入栈s
while(栈s不为空)
后序遍历将T的所有左节点入栈s
p=NULL
while(s不为空及flag不为0)
if(T->rchild等于p)
if T->data为数字
将其入栈s1中
else
为运算符则用switc处理运算符
a b为s1栈顶的两个数
再用运算符处理a b (+-*/均为一样的处理)
else
T=T->rchild;
flag=0;
end while
return s1.top();
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
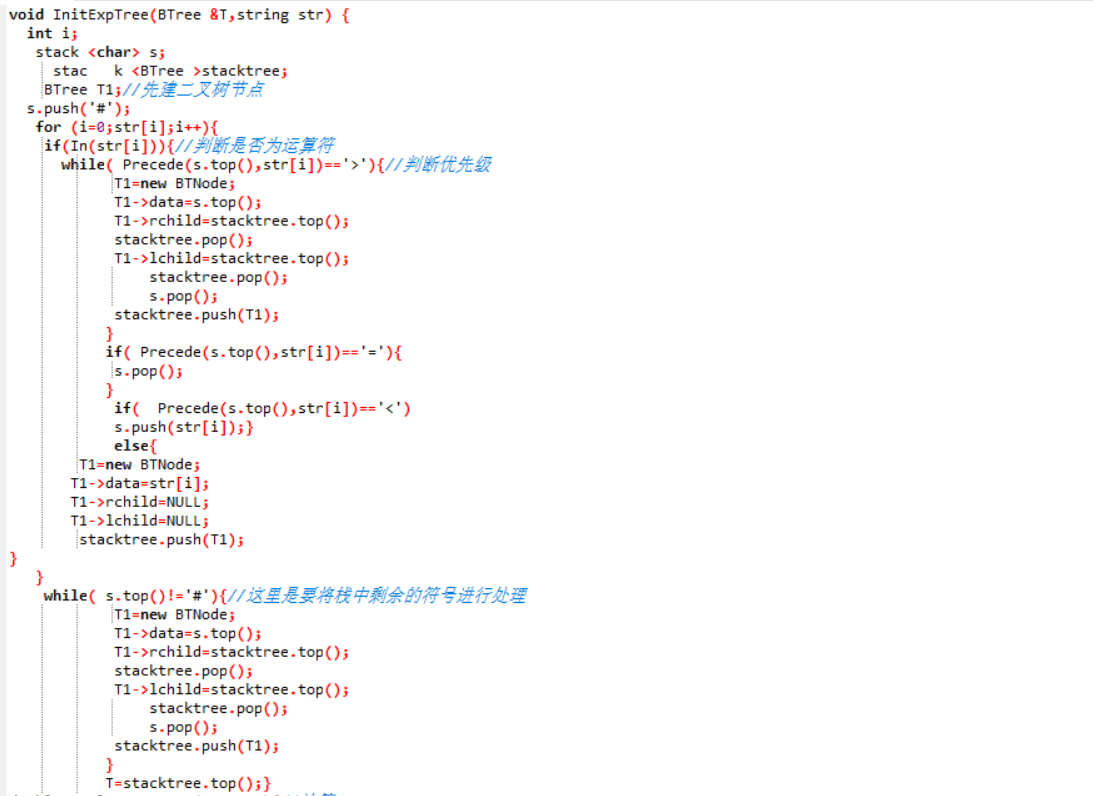
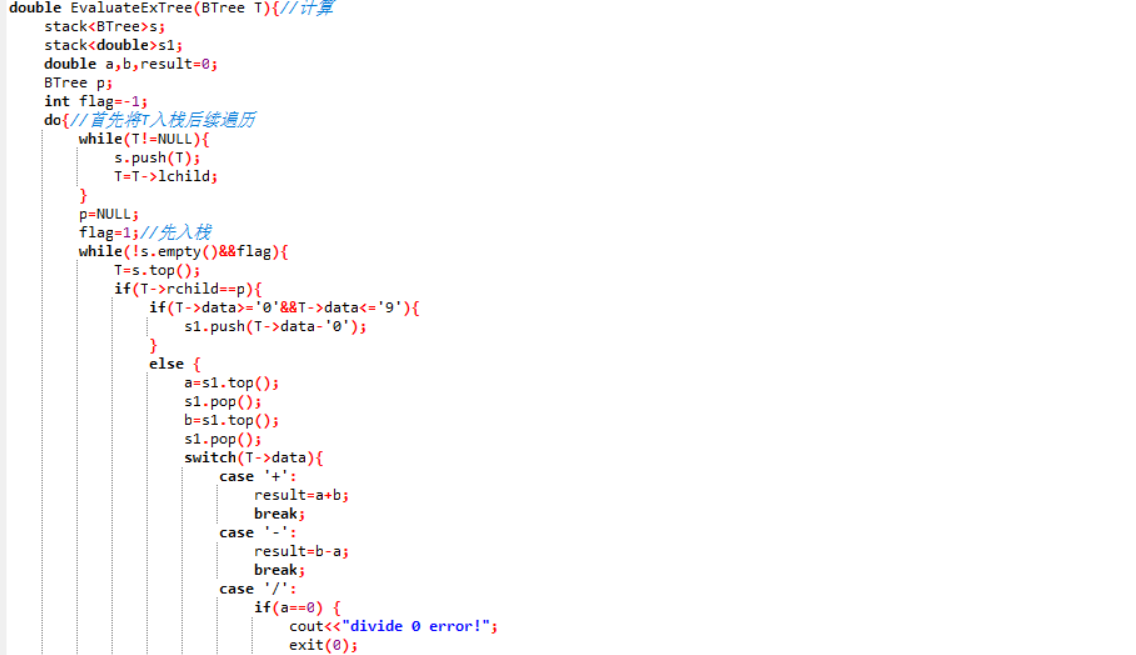

2.4 PTA提交列表说明。
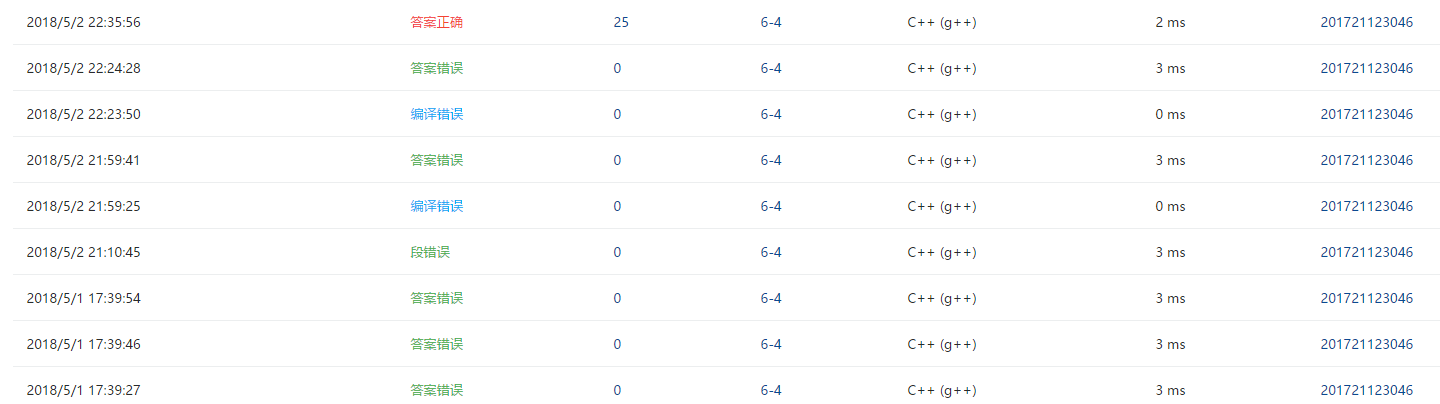
- 建树的时候没有处理栈中剩余的运算符,也就是老师在课上说的伪代码的不足之处
- 计算的函数我是问舍友的,主要是非递归的后序遍历,运用栈来处理方法比较巧妙
2.1 题目3:7-8 jmu-ds-二叉树叶子结点带权路径长度和(25 分)
2.2 设计思路(伪代码或流程图)
这里主要写递归建树和计算WPL的函数
BTree CreateBTree(string str,int n) 建树
建立新节点BT
if(str(n等于#)
return NULL
else if(n>=l)防止超出长度,这里的l是全局变量为str的长度
return NULL
else
BT->data的值为str[n];
递归建立左子树CreateBTree(str,2*n);
递归建立右子树CreateBTree(str,2*n+1)
int PreOrder( BTree BT,int n )计算WPL二叉树
定义静态变量wpl
n代表树的高度
if(BT不为空){
if(BT为叶节点)
计算wpl
递归计算左子树
递归计算右子树
}
return wpl
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
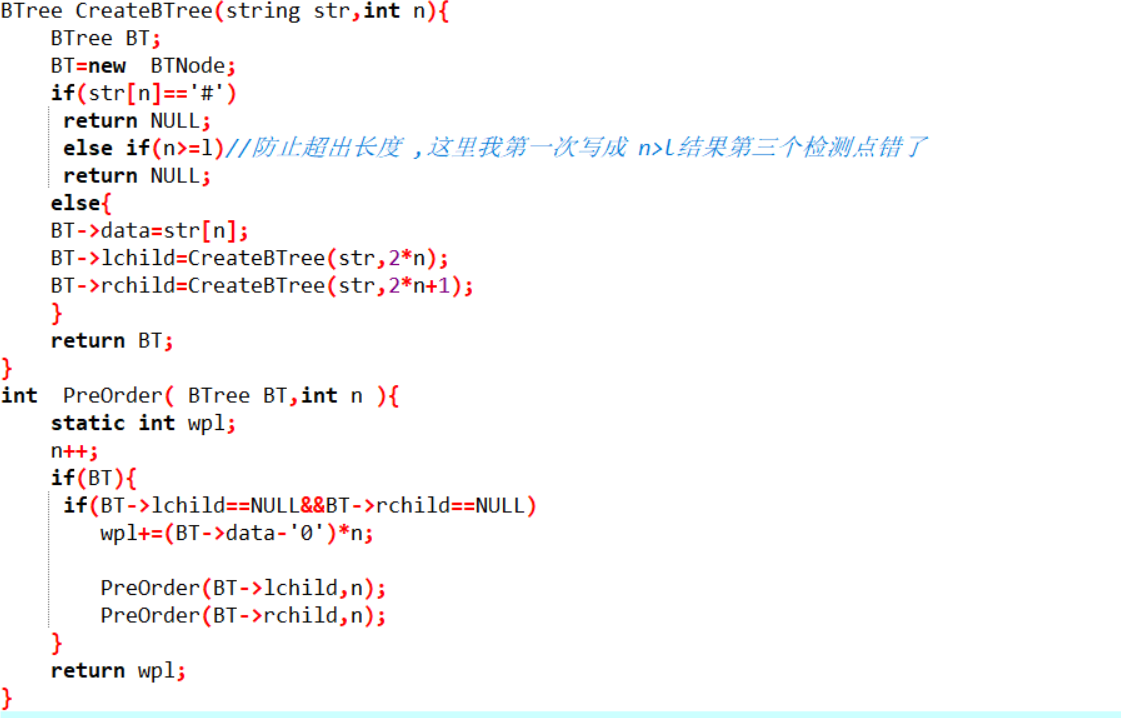
2.4 PTA提交列表说明。

- 这道题我在建树的时后没有考虑到递归到超出长度的情况,导致段错误,后来我设置了一个全局变量l来存储长度
用来限定递归的范围。 - 还有就是WPl的值我起先是用函数里的参数来计算结果递归直接错误,用静态变量直接解决了。
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名
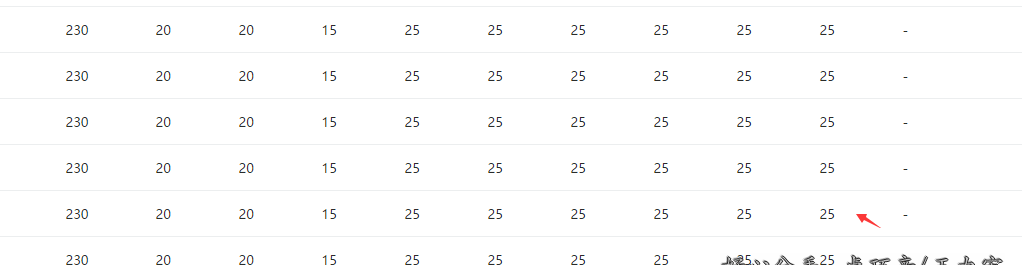
3.2 我的得分:230
4. 阅读代码(必做,1分)
代码
题目大意
有一棵二叉的苹果树,(既然是树的话那就有n个节点和n-1个枝条),现在我们要剪枝,使得留下m个枝条,但是有些枝条上是有苹果的,求剪哪些枝条才能够保住最多的苹果。(虽然题目没说,但由于这是一棵苹果树,你只能剪叶子节点的枝条,所以是不能贪心的)
输入格式
第1行2个数,N和Q(1<=Q<= N,1<N<=100)。
N表示树的结点数,Q表示要保留的树枝数量。接下来N-1行描述树枝的信息。
每行3个整数,前两个是它连接的结点的编号。第3个数是这根树枝上苹果的数量。
每根树枝上的苹果不超过30000个。
输出格式
剩余苹果的最大数量。
输入样例
5 2
1 3 1
1 4 10
2 3 20
3 5 2021
代码
[cpp] view plain copy
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<queue>
#include<climits>
using namespace std;
int n,m;
int l[101],r[101],a[101];
int bian[101][4],sum[101][4];
int f[101][101];
bool vis[101],vv[101][101];
void dfs(int now){//转化成二叉树
int i;
vis[now]=1;
for(i=1;i<=bian[now][0];i++)//寻找子节点
if(vis[bian[now][i]]==0){
if(l[now]==0){
l[now]=bian[now][i];
a[l[now]]=sum[now][i];//挪动苹果
dfs(bian[now][i]);
}
else{
r[now]=bian[now][i];a[r[now]]=sum[now][i];
dfs(bian[now][i]);
}
}
}
void find(int i,int j){
int k;
if(vv[i][j]==1)return;
vv[i][j]=1;//记忆化,如果已经搜出了f[i][j]就不用搜了
if(j==0||i==0)return;
for(k=0;k<=j-1;k++){
find(l[i],k);
find(r[i],j-k-1);//先弄出你需要的f
f[i][j]=max(f[i][j],f[l[i]][k]+f[r[i]][j-k-1]+a[i]);//dp方程
}
}
int main()
{
int i,j,x,y,apple;
scanf("%d%d",&n,&m);
for(i=1;i<=n-1;i++){
scanf("%d%d%d",&x,&y,&apple);
bian[x][0]++;bian[x][bian[x][0]]=y;sum[x][bian[x][0]]=apple;
bian[y][0]++;bian[y][bian[y][0]]=x;sum[y][bian[y][0]]=apple;
}
dfs(1);
m++;//要选择根节点1
find(1,m);
printf("%d",f[1][m]);
return 0;
}
- 链接 https://blog.csdn.net/litble/article/details/63252961
- 烦恼的是苹果是长在枝条上的,其实你可以把苹果挪到这个枝条连接的子节点上,因为如果减去这个枝条,就不会保留子节点。那么我们就从选枝条变成了选节点。并且由于一定要留根节点,所以m++.
5. 代码Git提交记录截图



 posted on
posted on
